15 câu Dạng 1: Chứng minh hai mặt phẳng song song có đáp án

226 người thi tuần này 4.6 4.1 K lượt thi 15 câu hỏi 60 phút

Câu 1

Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của $Δ A B C, Δ A C D, Δ A B D .$
Chứng minh rằng $(M N P) // (B C D) .$

Xem đáp án

Lời giải

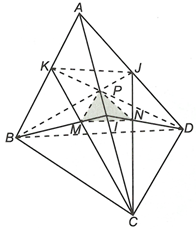
Cho tứ diện ABCD có M, N, P lần lượt là trọng tâm của ABC, ACD, ABD . Chứng minh rằng (MNP) // (BCD) (ảnh 1)

Gọi I, J, K lần lượt là trung điểm AC, AD, AB.

Xét $Δ I B D$ có $\frac{I M}{I B} = \frac{I N}{I D} = \frac{1}{3}$ nên $M N // B D .$

Suy ra $M N // (B C D) .$

Xét $Δ J B C$ có $\frac{I M}{I B} = \frac{I N}{I D} = \frac{1}{3}$ nên $N P // B C .$

Suy ra $N P // (B C D) .$

Ta có $\{\begin{cases} M N // (B C D) \\ N P // (B C D) \\ M N, N P \subset (M N P), M N \cap N P = \{N\} \end{cases}$

$\Rightarrow (M N P) // (B C D) .$

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC.

a) Chứng minh (MNP) // (ABCD)

Xem đáp án

Lời giải

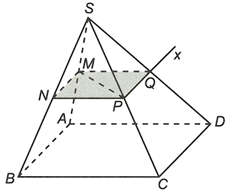
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm SA, SB, SC. a) Chứng minh (MNP) // (ABCD) (ảnh 1)

a) Ta có $M N // A B, A B \subset (A B C D) \Rightarrow M N // (A B C D) .$

Tương tự $N P // B C, B C \subset (A B C D) \Rightarrow N P // (A B C D) .$

Ta có $\{\begin{cases} M N // (A B C D) \\ N P // (A B C D) \\ M N, N P \subset (M N P), M N \cap N P = \{N\} \end{cases} \Rightarrow (M N P) // (A B C D) .$

Câu 3

b) Gọi Q là giao điểm của (MNP) và SD. Chứng minh tứ giác MNPQ là hình bình hành.

Xem đáp án

Lời giải

b) Ta có $S D \subset (S C D) .$

Xét hai mặt phẳng $(M N P)$ và $(S C D)$ có $P \in (M N P) \cap (S C D)$

Ta có $\{\begin{cases} C D \subset (S C D), M N \subset (M N P) \\ M N // C D \end{cases} \Rightarrow (M N P) \cap (S C D) = P x$

sao cho $P x // C D // M N .$ (vì MN // AB theo tính chất đường trung bình và CD // AB)

Trong $(S C D)$ gọi $P x \cap C D = \{Q\} .$ Suy ra $(M N P) \cap C D = \{Q\} .$

Ta có $(M N P) \cap (S C D) = P Q$ nên $P Q // C D // M N$ suy ra Q là trung điểm của SD và $M N = \frac{1}{2} A B = \frac{1}{2} C D = P Q .$

Vậy tứ giác MNPQ là hình bình hành (cặp cạnh đối song song và bằng nhau).

Câu 4

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của A'B' và AB. Chứng minh (AMC') // (CNB')

Xem đáp án

Lời giải

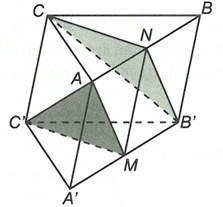
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của A'B' và AB. Chứng minh (AMC') // (CNB') (ảnh 1)

Ta có $M N // A A^{'}, A A^{'} // C C^{'} \Rightarrow M N // C C^{'}$ và theo tính chất hình lăng trụ thì $M N = C C^{'}$ nên tứ giác $M N C C^{'}$ là hình bình hành và $C N // M C^{'} .$

$\{\begin{cases} C N // M C^{'} \\ M C^{'} \subset (A M C^{'}) \end{cases} \Rightarrow C N // (A M C^{'}) .$

Mặt khác $A N // B^{'} M, A N = B^{'} M$ nên tứ giác $A N B^{'} M$ là hình bình hành và $N B^{'} // M A .$

Ta có $\{\begin{cases} N B^{'} // M A \\ M A \subset (A M C^{'}) \end{cases} \Rightarrow N B^{'} // (A M C^{'}) .$

Lại có

\{\begin{cases} C N // (A M C^{'}) \\ N B^{'} // (A M C^{'}) \\ C N, N B^{'} \subset (C N B^{'}) \\ C N \cap N B^{'} = \{N\} \end{cases} \Rightarrow (A M C^{'}) // (C N B^{'}) .

Câu 5

Cho hình lập phương ABCD.A'B'C'D', có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD'. Chứng minh rằng (MNP) song song với (ACD')

Xem đáp án

Lời giải

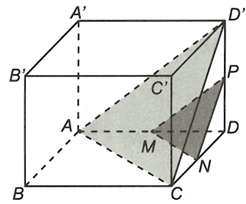
Cho hình lập phương ABCD.A'B'C'D', có M, N, P lần lượt là trung điểm của các cạnh AD, DC, DD'. Chứng minh rằng (MNP) song song với (ACD') (ảnh 1)

Xét $Δ A D D^{'}$ có $M P // A D^{'},$ mà $A D^{'} \subset (A C D^{'}) \Rightarrow M P // (A C D^{'}) .$

Tương tự trong $Δ A C D$ có $M N // A C,$ mà $A C \subset (A C D^{'}) \Rightarrow M N // (A C D^{'})$

Ta có $\{\begin{cases} M P // (A C D^{'}) \\ M N // (A C D^{'}) \\ M N, M P \subset (M N P) \\ M N \cap M P = \{M\} \end{cases} .$

Suy ra $(M N P) // (A C D^{'}) .$

Câu 6

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD.

a) Chứng minh rằng (OMN) song song với (SBC)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

b) Gọi K là trung điểm OM. Chứng minh NK // (SBC)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M, N lần lượt cắt AD và AF tại M' và N'.

a) (ADF) // (BCE)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

A. $O M // S C .$

B. $M N // (S B C) .$

C. $(O M N) // (S B C) .$

D. $O N \cap C B \neq \emptyset .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử