ĐGTD ĐH Bách khoa - Tư duy Toán học - Bài toán tiếp tuyến của đồ thị và sự tiếp xúc của hàm số
44 người thi tuần này 4.6 1.4 K lượt thi 21 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 15)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 14)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 13)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 12)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 11)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 10)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 9)
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 8)
Danh sách câu hỏi:
Lời giải
Ta có
⇒ Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ là
Đáp án cần chọn là: C
Lời giải
Đối với hàm số thì
⇒ Hệ số góc của tiếp tuyến luôn dương.
Đối với hàm số: thì
⇒ Hệ số góc của tiếp tuyến luôn dương.
Đối với hàm số
⇒ Hệ số góc của tiếp tuyến luôn dương.
Xét hàm số Có giao điểm của đồ thị hàm số với trục tung là: A(0;1)
Có
⇒ Hệ số góc của tiếp tuyến tại A có hệ số âm.
Đáp án cần chọn là: D
Lời giải
Hoành độ tiếp điểm của hai đồ thị hàm số là nghiệm của hệ phương trình:
Vậy là hoành độ điểm tiếp xúc.
Đáp án cần chọn là: B
Lời giải
Bước 1: Gọi tiếp điểm của tiếp tuyến với đồ thị hàm số là A(0;2).
Bước 2: Phương trình tiếp tuyến tại điểm A có dạng
Ta có Do đó phương trình tiếp tuyến là
Đáp án cần chọn là: B
Lời giải
Ta có: hoặc hoặc
Ta có bảng biến thiên
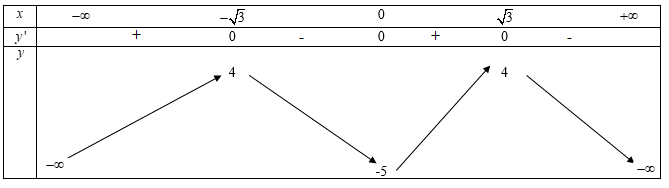
Quan sát bảng biến thiên ta thấy tiếp điểm là (0;−5) và .
Vậy phương trình đường tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là
Đáp án cần chọn là: B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. và
B. và
C. và
D. và
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.15
B.−27
C.12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. hoặc
B. M(2;3) hoặc M(0;1)
C. hoặc
D. M(2;3) hoặc
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.