299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P10)
25 người thi tuần này 5.0 25.5 K lượt thi 10 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
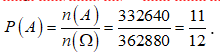
Lời giải
Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
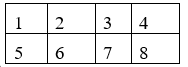
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()
Lời giải
Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là = 720 số
Gọi là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: 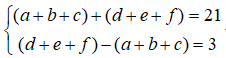
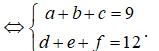
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là:
![]()
Lời giải
Chọn C
Số cách chọn của An là ; số cách chọn của Bình là . Vậy số phần tử của không gian mẫu là: ![]()
Gọi A là biến cố “ Hai bộ ba số An và Bình chọn ra có nhiều nhất một số giống nhau”.
TH1: Không có số nào giống nhau thì có cách chọn.
TH2: Có một số giống nhau thì có cách chọn.
Do đó ![]()
Vậy xác suất cần tìm là:
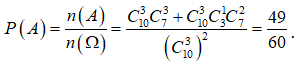
Lời giải
Chọn B
Số phần tử của tập hợp E là ![]()
Vì ![]()
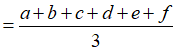
![]()
Mà chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại ra một số chia hết cho 3. Ta có 3 trường hợp sau:
1) Trường hợp 1:
Loại bỏ số 0, khi đó a + b = c + d = e + f = 7
Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.
Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.
Trường hợp này có 48 số.
2) Trường hợp 2:
Loại bỏ số 3, khi đó a + b = c + d = e + f = 6
Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.
Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.
Trường hợp này có 40 số.
3) Trường hợp 3:
Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.
Vậy trong tập hợp E có tất cả 48 + 40 + 40 = 128 số có dạng sao cho a + b = c + d = e + f
Xác suất cần tìm là: ![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.