Đề số 9

Thi Online [Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Đề số 9

10634 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?

A. $y = \frac{x}{1 - x}$

B. $y = \frac{x + 1}{1 - x}$

C. $y = \frac{x + 1}{x - 1}$

D. $y = \frac{x}{x - 1}$

Xem đáp án

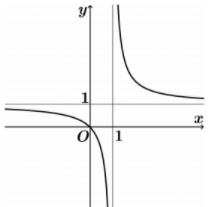
Dựa vào đồ thị hàm số ta thấy: Đồ thị có đường TCN y=1 và TCĐ x=1.

Do đó loại đáp án A và B.

Đồ thị hàm số đi qua điểm O(0;0) nên loại đáp án C.

Đáp án A.

Câu 2:

Tìm tất cả các điểm M nằm trên đồ thị hàm số $y = \frac{x - 2}{x + 1}$ mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng $d : y = 3 x + 10$ .

A. $M (3; \frac{1}{4})$

B. $M (0; - 2)$ hoặc \[M\left( { - 2;4} \right)\]

C. $M (- 2; 4)$

M (- \frac{5}{2}; 3)

Xem đáp án

TXĐ: $D = ℝ \ {- 1}$ .

Gọi $M (x_{0}; \frac{x_{0} - 2}{x_{0} + 1}) (x_{0} \neq - 1)$ thuộc đồ thị hàm số $y = \frac{x - 2}{x + 1}$ .

Ta có $y = \frac{x - 2}{x + 1} \Rightarrow y^{'} = \frac{3}{{(x + 1)}^{2}}$ nên tiếp tuyến của đồ thị hàm số tại $M (x_{0}; \frac{x_{0} - 2}{x_{0} + 1})$ có hệ số góc là $k = y^{'} (x_{0}) = \frac{3}{{(x_{0} + 1)}^{2}}$ .

Vì tiếp tuyến tại M song song với đường thẳng $d : y = 3 x + 10$ nên \[\frac{3}{{{{\left( {{x_0} + 1} \right)}^2}}} = 3 \Leftrightarrow {\left( {{x_0} + 1} \right)^2} = 1\]

$\Leftrightarrow [\begin{array}{l} x_{0} + 1 = 1 \\ x_{0} + 1 = - 1 \end{array} \Leftrightarrow [\begin{array}{l} x_{0} = 0 \\ x_{0} = - 2 \end{array} (t m)$ $\Rightarrow [\begin{array}{l} M (0; - 2) \\ M (- 2; 4) \end{array}$

Đáp án B.

Câu 3:

Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm $I (1; - 1)$ . Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.

A. $M (1 + \sqrt{2}; - 1 - \sqrt{2})$ và $M (1 - \sqrt{2}; - 1 + \sqrt{2})$ .

B. $M (- 1; 0)$ và $M (3; - 2)$ .

C. $M (\sqrt{2}; - 3 - 2 \sqrt{2})$ và $M (- \sqrt{2}; 2 \sqrt{2} - 3)$ .

D. $M (2; - 3)$ và $M (0; 1)$ .

Xem đáp án

TXĐ: $D = ℝ \ {1}$ .

Gọi $M (x_{0}; \frac{x_{0} + 1}{1 - x_{0}}) (x_{0} \neq 1)$ thuộc đồ thị hàm số $y = \frac{x + 1}{1 - x}$ .

Ta có $y = \frac{x + 1}{1 - x} \Rightarrow y^{'} = \frac{2}{{(1 - x)}^{2}}$ nên tiếp tuyến của đồ thị hàm số tại $M (x_{0}; \frac{x_{0} + 1}{1 - x_{0}})$ có hệ số góc là $k = y^{'} (x_{0}) = \frac{2}{{(1 - x_{0})}^{2}}$ .

⇒ Phương trình tiếp tuyến tại M là: $y = \frac{2}{{(1 - x_{0})}^{2}} (x - x_{0}) + \frac{x_{0} + 1}{1 - x_{0}}$ $\Leftrightarrow \frac{2}{{(1 - x_{0})}^{2}} x - y - \frac{2 x_{0}}{{(1 - x_{0})}^{2}} + \frac{x_{0} + 1}{1 - x_{0}} = 0$ , có 1 VTCP là $\vec{u} = (1; \frac{2}{{(1 - x_{0})}^{2}})$ .

Ta có: $\vec{I M} = (x_{0} - 1; \frac{x_{0} + 1}{1 - x_{0}} + 1) = (x_{0} - 1; \frac{2}{1 - x_{0}})$ .

Vì tiếp tuyến tại M vuông góc với IM nên $\vec{u} . \vec{I M} = 0$ .

\[ \Leftrightarrow \left( {{x_0} - 1} \right) + \frac{4}{{{{\left( {1 - {x_0}} \right)}^3}}} = 0\] $\Leftrightarrow \frac{4}{{(1 - x_{0})}^{3}} = 1 - x_{0} \Leftrightarrow {(1 - x_{0})}^{4} = 4$

$\Leftrightarrow [\begin{array}{l} 1 - x_{0} = \sqrt{2} \\ 1 - x_{0} = - \sqrt{2} \end{array} \Leftrightarrow [\begin{array}{l} x_{0} = 1 - \sqrt{2} \\ x_{0} = 1 + \sqrt{2} \end{array}$

⇒ $M (1 + \sqrt{2}; - 1 - \sqrt{2})$ và $M (1 - \sqrt{2}; - 1 + \sqrt{2})$ .

Đáp án A.

Câu 4:

Mệnh đề nào dưới đây về hàm số $y = {(x^{2} - 4)}^{2} + 1$ là đúng?

A. Nghịch biến trên $(- 2; 2)$

B. Đồng biến trên $ℝ$

C. Đồng biến trên $(- \infty; - 2)$ và\[\left( {2; + \infty } \right)\]

D. Đồng biến trên $(- 2; 0)$ và \[\left( {2; + \infty } \right)\].

Xem đáp án

TXĐ: $D = ℝ$ .

Ta có: $y = {(x^{2} - 4)}^{2} + 1 \Rightarrow y^{'} = 2 (x^{2} - 4) .2 x$ .

Cho $y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x^{2} - 4 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 2 \end{array}$ .

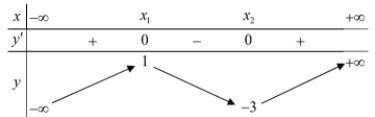
BXD y':

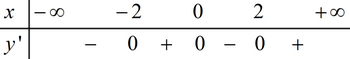
Dựa vào BXD ta thấy hàm số đồng biến trên \[\left( { - \infty ; - 2} \right);{\mkern 1mu} {\mkern 1mu} \left( {0;2} \right)\]; nghịch biến trên $(- 2; 0); (2; + \infty)$ .

Đáp án D.

Câu 5:

Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.

A. $\frac{π}{6}$

B. $\frac{4 \sqrt{3} π}{27}$

C. $\frac{4 π}{81}$

D. $\frac{\sqrt{3} π}{54}$

Xem đáp án

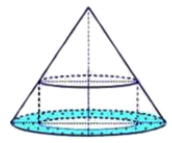
Giả sử thiết diện qua trục là tam giác SAB và O là tâm mặt đáy của hình nón, ta có tam giác SAB đều cạnh 1 nên $S O = \frac{\sqrt{3}}{2}$ .

Gọi I là tâm khối cầu nội tiếp trong hình nón, dễ thấy O chính là tâm tam giác đều SAB, do đó bán kính khối cầu là $R = I O = \frac{2}{3} S O = \frac{2}{3} . \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{3}$ .

Vậy thể tích khối cầu nội tiếp trong hình nón là $V = \frac{4}{3} π R^{3} = \frac{4}{3} π {(\frac{\sqrt{3}}{3})}^{3} = \frac{4 \sqrt{3} π}{27}$ .

Đáp án B.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đánh giá trung bình

Thi Online [Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề)

Đề số 9

Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?

Tìm tất cả các điểm M nằm trên đồ thị hàm số y=x−2x+1 mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng d:y=3x+10.

Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm I(1;−1). Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.

Mệnh đề nào dưới đây về hàm số y=(x2−4)2+1 là đúng?

Cho một hình nón có thiết diện qua trục là một tam giác đều cạnh bằng 1. Tính thể tích khối càu nội tiếp trong hình nón.

Bài thi liên quan:

Đề số 1

Đề số 2

Đề số 3

Đề số 4

Đề số 5

Đề số 6

Đề số 7

Đề số 8

Đề số 10

Đề số 11

Đề số 12

Đề số 13

Đề số 14

Đề số 15

Đề số 16

Đề số 17

Đề số 18

Đề số 19

Đề số 20

Đề số 21

Đề số 22

Đề số 23

Đề số 24

Đề số 25

Đề số 26

Đề số 27

Đề số 28

Đề số 29

Đề số 30

Các bài thi hot trong chương:

Bình luận

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Số điện thoại hiện tại của bạn có vẻ không hợp lệ, vui lòng cập nhật số mới để hể thống kiểm tra lại!

Tìm tất cả các điểm M nằm trên đồ thị hàm số $y = \frac{x - 2}{x + 1}$ mà tiếp tuyến của đồ thị tại điểm đó song song với đường thẳng $d : y = 3 x + 10$ .

Cho hàm số \[y = \frac{{x + 1}}{{1 - x}}\] và điểm $I (1; - 1)$ . Tìm tất cả các điểm M nằm trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với IM.

Mệnh đề nào dưới đây về hàm số $y = {(x^{2} - 4)}^{2} + 1$ là đúng?