160 bài trắc nghiệm Mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

43 người thi tuần này 4.6 7.6 K lượt thi 40 câu hỏi 50 phút

Câu 1/40

Trong không gian Oxyz, cho hai điểm I(1;1;1) và A(1;2;3). Phương trình của mặt cầu có tâm I và đi qua A là:

A. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 29$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5$

C. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 25$

D. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 5$

Lời giải

Chọn đáp án B.

Có $IA = R = \sqrt{1^{2} + 2^{2}} = 5$

Khi đó mặt cầu tâm I đi qua A có phương trình ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 5$

Câu 2/40

Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng:

A. $\frac{\sqrt{3} π α^{3}}{3}$

B. $\frac{\sqrt{3} π α^{3}}{2}$

C. $\frac{2 π α^{3}}{3}$

D. $\frac{π α^{3}}{3}$

Lời giải

Chọn đáp án A.

Có $l = 2 a, r = a$

$\Rightarrow h = \sqrt{l^{2} - r^{2}} = a \sqrt{3}$

Khi đó thể tích khối nón là:

$V = \frac{1}{3} π r^{2} h = \frac{\sqrt{3} π α^{3}}{3}$

Câu 3/40

Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là $r_{1}, h_{1}, r_{2}, h_{2}$ thỏa mãn $r_{2} = \frac{1}{2} r_{1}, h_{2} = 2 h_{1}$ (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng $30 c m^{3}$ thể tích của khối trụ (H1) bằng:

A. $24 c m^{3}$

B. $15 c m^{3}$

C. $20 c m^{3}$

D. $10 c m^{3}$

Lời giải

Chọn đáp án C.

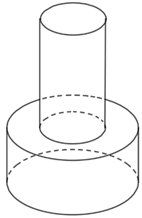
Thể tích khối trụ (H1) là:

$V_{1} = π {r_{1}}^{2} h_{1}$

Thể tích khối trụ (H2) là:

$V_{2} = π {r_{2}}^{2} h_{2} = \frac{1}{2} π {r_{1}}^{2} h_{1}$

Theo giả thiết ta có:

$V_{1} + V_{2} = 30 c m^{3} \Leftrightarrow \frac{3}{2} V_{1} = 30 c m^{3} \Leftrightarrow V_{1} = 20 c m^{3}$

Câu 4/40

Cho hình nón có độ dài đường sinh gấp đôi chiều cao và bán kính đáy bằng $\sqrt{3}$ . Diện tích xung quanh của hình nón đã cho bằng:

A. $4 \sqrt{3} π$

B. $(3 + 2 \sqrt{3}) π$

C. $2 \sqrt{3} π$

D. $\sqrt{3} π$

Lời giải

Chọn đáp án C.

Có $\{\begin{cases} r = \sqrt{3} \\ l = 2 h \\ l^{2} = h^{2} + r^{2} \end{cases} \Leftrightarrow \{\begin{cases} r = \sqrt{3} \\ h = 1 \\ l = 2 \end{cases}$

$S_{x q} = π r l = 2 \sqrt{3} π$

Câu 5/40

Hai hình nón bằng nhau có chiều cao bằng 2 dm, được đặt như hình vẽ bên (mỗi hình đều đặt thẳng đứng với đỉnh nằm phía dưới). Lúc đầu, hình nón trên chứa đầy nước và hình nón dưới không chứa nước. Sau đó, nước được chảy xuống hình nón dưới thông qua lỗ trống ở đỉnh của hình nón trên. Hãy tính chiều cao của nước trong hình nón dưới tại thời điểm khi mà chiều cao của nước trong hình nón trên bằng 1 dm.

A. $\sqrt[3]{7}$

B. $\frac{1}{3}$

C. $\sqrt[3]{5}$

D. $\frac{1}{2}$

Lời giải

Chọn đáp án A.

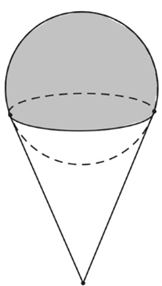
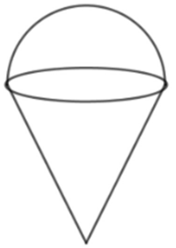
Lượng nước trong nón 1 đã chảy xuống nón 2 bằng:

$\frac{π r^{2} . 2}{3} - \frac{π . {(\frac{r}{2})}^{2} . 1}{3} = \frac{7 π r^{2}}{12}$

Chiều cao nước nón 2 là h thì bán kính đáy nước trong nón 2 bằng:

$\frac{h}{2} = \frac{r^{'}}{r} \Rightarrow r^{'} = \frac{r h}{2}$

Thể tích nước trong nón 2 bằng:

$\frac{π {(\frac{r h}{2})}^{2} . h}{3} = \frac{7 π r^{2}}{12} \Leftrightarrow h = \sqrt[3]{7}$

Câu 6/40

Cho hình chữ nhật ABCD có AB = 2AD. Quay hình chữ nhật đã cho quanh AD và AB ta được hai hình trụ tròn xoay có thể tích lần lượt là V₁, V₂. Mệnh đề nào dưới đây đúng?

A. $V_{1} = 4 V_{2}$

B. $V_{2} = 4 V_{1}$

C. $V_{2} = 2 V_{1}$

D. $V_{1} = 2 V_{2}$

Lời giải

Chọn đáp án D.

Quay quanh AD thu được trụ có r = AB, h = AD; quay quanh AB thu được trụ có r = AD, h = AB.

Vậy $\frac{V_{1}}{V_{2}} = \frac{π . A B^{2} . A D}{π . A D^{2} . A B} = \frac{A B}{A D} = 2$

Câu 7/40

Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?

A. $150 c m^{3}$

B. $250 c m^{3}$

C. $200 c m^{3}$

D. $300 c m^{3}$

Lời giải

Chọn đáp án B.

Hộp hình trụ có R = h = 10. Gọi a là độ dài cạnh hình vuông (tấm bìa) đã cho. Gọi AB, CD lần lượt là cạnh hình vuông trên mặt đáy; cạnh trên mặt phía trên của hộp. Gọi E, F lần lượt là hình chiếu vuông góc của C, D xuống mặt đáy.

Ta có: $\{\begin{cases} E F = C D = A B \\ E F / / C D / / A B \end{cases}$

$\Rightarrow A E F B là hình chữ nhật nội tiếp đường tròn có bán kính R = 10 .$

Do đó $A B^{2} + B F^{2} = A F^{2}$

$\Leftrightarrow A B^{2} + B F^{2} = 4 R^{2} \Leftrightarrow a^{2} + B F^{2} = 4 R^{2} (1)$

Mặt khác theo pitago có:

$B D^{2} = B F^{2} + F D^{2} \Leftrightarrow a^{2} = B F^{2} + h^{2} (2)$

Từ (1) và (2) có:

$4 R^{2} - a^{2} = a^{2} - h^{2} \Leftrightarrow a^{2} = \frac{h^{2} + 4 R^{2}}{2} = \frac{10^{2} + 4 \times 10^{2}}{2} = 250$

Câu 8/40

Mặt cầu ngoại tiếp tứ diện vuông O.ABC có OA = OB = OC = a có bán kính bằng:

A. $\frac{a}{2}$

B. $\frac{\sqrt{3} a}{2}$

C. $\frac{\sqrt{2} a}{2}$

D. $\frac{\sqrt{3} a}{4}$

Lời giải

Chọn đáp án B.

Có $R = \frac{\sqrt{O A^{2} + O B^{2} + O C^{2}}}{2} = \frac{\sqrt{3} a}{2}$

Câu 9/40

Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần S_tp của hình nón khi quay tam giác ABC xung quanh trục AC.

A. $S_{t p} = 4 π$

B. $S_{t p} = 24 π$

C. $S_{t p} = 72 π$

D. $S_{t p} = 48 π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/40

Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng $\frac{1}{8}$ thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ?

A. $2, 6 m^{2}$

B. $1, 5 m^{2}$

C. $3, 4 m^{2}$

D. $1, 7 m^{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/40

Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Tính góc α ở đỉnh của hình nón.

A. $α = 120 °$

B. $α = 30 °$

C. $α = 60 °$

D. $α = 90 °$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/40

Cho hình chóp S.ABC có SA=SB=SC=a, $∠ A S B = ∠ A S C = 90 °$ , $∠ B S C = 60 °$ . Tính diện tích mặt cầu ngoại tiếp hình chóp đã cho.

A. $\frac{7 π a^{2}}{6}$

B. $\frac{7 π a^{2}}{3}$

C. $\frac{7 π a^{2}}{18}$

D. $\frac{7 π a^{2}}{12}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/40

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và AB=2, AC=4,SA= $\sqrt{5}$ . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là:

A. R= $\frac{5}{2}$

B. R=5

C. R= $\frac{10}{3}$

D. R= $\frac{25}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/40

Người ta thả một viên bi sắt có dạng hình cầu với bán kính nhỏ hơn 4,5cm vào một chiếc cốc hình trụ đang chứa nước thì viên bi sắt đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong lòng cốc bằng 4,5cm. Bán kính của viên bi sắt đó bằng:

A. 4,2cm.

B. 3,6cm.

C. 2,6cm.

D. 2,7cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/40

Một que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng:

A. 3.

B. 2.

C. $\frac{4}{3}$

D. $\frac{16}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16/40

Một chiếc kem gồm hai phần: phần phía dưới là một khối nón có chiều cao gấp đôi bán kính đáy; phần phía trên là một nửa khối cầu có đường kính bằng đường kính đáy của khối nón bên dưới. Thể tích phần kem phía trên bằng 200cm³ , thể tích của cả chiếc kem đã cho bằng:

A. 400cm³

B. 300cm³

C. 50cm³

D. 350cm³

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17/40

Cho tam giác ABC vuông tại A, AB=6, AC=8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là:

A. $\frac{96}{3} π$

B. $96 π$

C. $\frac{384}{5} π$

D. $\frac{1152}{5} π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18/40

Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R), (O',R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O'AB là tam giác đều và (O'AB) hợp với đường tròn O một góc $60 °$ . Tính diện tích xung quanh của hình trụ.

A. $\frac{π \sqrt{7} R^{2}}{7}$

B. $\frac{4 π \sqrt{7} R^{2}}{7}$

C. $\frac{2 π \sqrt{7} R^{2}}{7}$

D. $\frac{6 π \sqrt{7} R^{2}}{7}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19/40

Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h, OB=R, OH=x ( 0<x<h). Tìm thể tích lớn nhất của hình trụ.

A. $\frac{4 π R^{2} h}{27}$

B. $\frac{2 π R^{2} h}{9}$

C. $\frac{2 π R^{2} h}{27}$

D. $\frac{4 π R^{2} h}{9}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20/40

Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy 1 góc $60 °$ . Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:

A. $\frac{π a^{2} \sqrt{10}}{4}$

B. $\frac{π a^{2} \sqrt{10}}{2}$

C. $\frac{π a^{2} \sqrt{5}}{2}$

D. $\frac{π a^{2} \sqrt{5}}{4}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 32/40 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hà Nội

ĐHQG Hồ Chí Minh

ĐH Bách Khoa Hà Nội

ĐHSP Hà Nội

Bộ Công an

Bộ Quốc phòng

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý