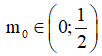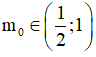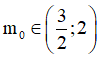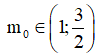175 câu Bài tập Số phức cơ bản, nâng cao có lời giải (P4)
62 người thi tuần này 4.6 26.3 K lượt thi 25 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án C
Phương pháp: Gọi ![]() là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
Lời giải chi tiết.
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng ![]() Khi đó ta có
Khi đó ta có
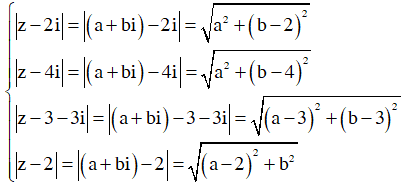
Từ giả thiết ta suy ra
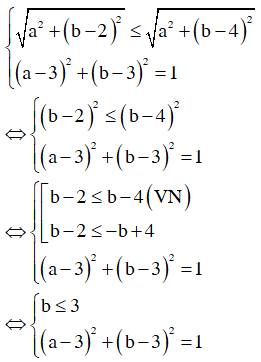
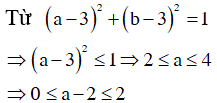
Do đó ![]()
Đẳng thức xảy ra khi và chỉ khi
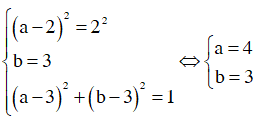
Chú ý. Đối với bài toán liên quan tới cực trị học sinh thường mắc phải sai lầm là quên tìm giá trị để cực trị xảy ra. Điều này có thể dẫn tới việc tìm sai giá trị lớn nhất nhỏ nhất
Lời giải
Đáp án D
Phương pháp
Biện luận để tìm trực tiếp nghiệm . Sử dụng giả thiết để tìm ra giá trị
Lời giải chi tiết.
Viết lại phương trình đã cho thành ![]()
Nếu Hay phương trình chỉ có một nghiệm. (Loại)
Nếu thì phương trình đã cho có hai nghiệm thực ![]()
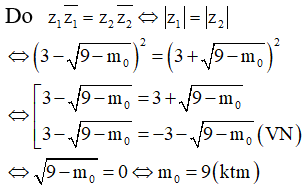
Nếu thì phương trình đã cho có hai nghiệm phức liên hợp là
![]()
Khi đó ![]()
Do đó thỏa mãn yêu cầu bài toán.
Do bài toán đòi hỏi nên ![]()
Vậy có 10 giá trị thỏa mãn.
Câu 3
A. ab=-2
B. ab=2
C. ab=1
D. ab=-1
Lời giải
Đáp án C
Phương pháp
Gọi số phức đã cho có dạng ![]() . Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
. Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
Lời giải chi tiết.
Ta có: ![]()
Do z không là số thực nên ta phải có (2)
Ta lại có
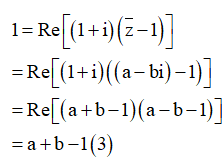
Từ (1), (2), (3) ta có hệ
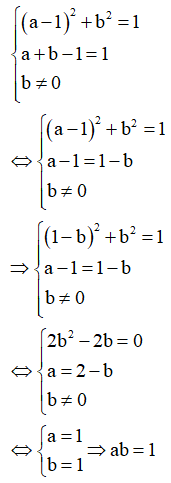
Lời giải
Đáp án B
Phương pháp
Từ giả thiết ta biến đổi để tìm được công thức của z. Dùng định nghĩa để tìm
Lời giải chi tiết.
Ta có:
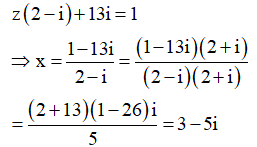
Do đó ![]()
Lời giải
Đáp án D
Phương pháp.Sử dụng giả thiết để tìm được ![]()
Thay vào ![]() và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
và sử dụng yêu cầu bài toán để biện luận và tìm giá trị của
Lời giải chi tiết.
Giả sử ![]() . Khi đó ta có
. Khi đó ta có
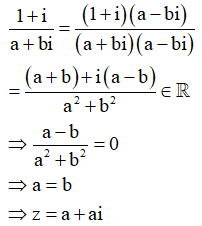
Thay vào ![]() Ta nhận được
Ta nhận được
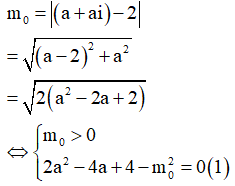
Để có đúng một nghiệm phức thỏa mãn bài toán thì phương trình (1) phải có duy nhất một nghiệm a.
Khi đó phương trình (1) phải thỏa mãn
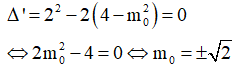
Kết hợp với điều kiện ![]() ta suy ra giá trị cần tìm là
ta suy ra giá trị cần tìm là ![]()
Sai lầm.Một bộ phận nhỏ học sinh vẫn có thể quên đưa ra điều kiện ![]() nên hai nghiệm là
nên hai nghiệm là ![]()
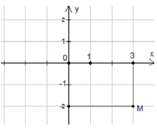
Câu 6
A. M thuộc tia Ox.
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox.
D. M thuộc tia đối của tia Oy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. maxT=
B. maxT=14
C. maxT=4
D. maxT=
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. maxT=
B. maxT=8
C. maxT=
D. maxT=4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. z=-3+2i
B. z=3+2i
C. z=-3-2i
D. z=3-2i
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. 22
B. 23
C. 45
D. 46
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.