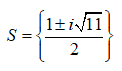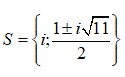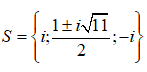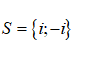175 câu câu Bài tập Số phức cơ bản, nâng cao có lời giải (P6)
41 người thi tuần này 4.6 26.3 K lượt thi 25 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. -2
B.
C.
D.
Lời giải
Đáp án C.
Ta có:
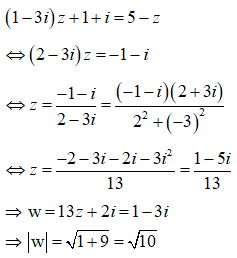
Lời giải
Đáp án B.
Ta có: z = (1-2i)(4-3i)-2+8i = -4-3i
Phần thực: –4, phần ảo: –3
![]()
Hai ý (3) và (4) sai.
Câu 3
A. Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(1; –2)
B. Tập hợp điểm biểu diễn các số phức z là đường tròn có bán kính R = 5
C. Tập hợp điểm biểu diễn các số phức z là đường tròn có đường kính bằng 10
D. Tập hợp điểm biểu diễn các số phức z là hình tròn có bán kính R = 5
Lời giải
Đáp án D.
Gọi ![]()
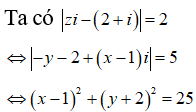
Vậy tập hợp điểm biểu diễn các số phức là đường tròn tâm I(1;-2) và bán kính R=5
Bình luận: Bài toán này ta dễ dàng nhận ra bằng phương pháp loại trừ nhất định 2 đáp án B và C đúng.
Mặt khác ![]()
Vậy biểu diễn hình học của z không thể là hình tròn:
Biểu diễn hình học của số phức.
Số phức z=a+bi được biểu diễn bởi điểm M(a;b) trong mặt phẳng Oxy.
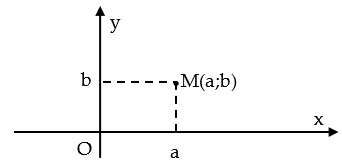
Câu 4
A. 12+2i
B. -2+12i
C. 6-4i
D. 12+4i
Lời giải
Đáp án A.
Do ![]() nên tập hợp điểm M là các điểm nằm ngoài đường tròn
nên tập hợp điểm M là các điểm nằm ngoài đường tròn ![]() và nằm trong đường tròn
và nằm trong đường tròn 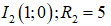
Dựa vào hình vẽ ta chứng minh được ![]()
Khi đó ![]()
Câu 5
A. M.m=25
B. M.m=20
C. M.m=30
D. M.m=24
Lời giải
Chọn D.
Dạng tổng quát: Cho số phức z thỏa mãn ![]() . Tính Min, Max của
. Tính Min, Max của ![]() .
.
Ta có: 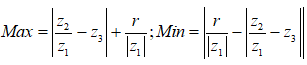
Áp dụng Công thức trên với ![]()
Ta được: Max=6; Min=4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 10
B. 30
C. 20
D. 40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. Đường tròn tâm I(3;4) R=12
B. Đường tròn tâm I(3;4) R=4
C. Đường tròn tâm I(3;-4) R=2
D. Đường tròn tâm I(3;4) R=8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. Tập hợp điểm biểu diễn các số phức z là đường tròn tâm I(1; –2)
B. Tập hợp điểm biểu diễn các số phức z là đường tròn có bán kính R = 5
C. Tập hợp điểm biểu diễn các số phức z là đường tròn có đường kính bằng 10
D. Tập hợp điểm biểu diễn các số phức là hình tròn có bán kính R = 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. (3;1)
B. (-1;3)
C. (2;-3)
D. (-3;2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. z là số thuần ảo
B. z có phần ảo là số nguyên tố
C. z có phần thực là số nguyên tố
D. z có tổng phần thực và phần ảo là 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. 2
B. 1
C. -2
D. 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.