Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 4)

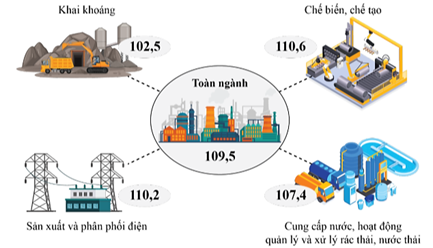
Ta có bảng thống kê tốc độ tăng trưởng của các ngành:

Dựa vào bảng số liệu trên ta có thể thấy tốc độ tăng trưởng cao nhất là ngành chế biến, chế tạo.

Chọn B

Vì \(G\left( {1\,;\,\,c\,;\,\,3} \right)\) là trọng tâm của tam giác \[ABC\] suy ra: \(\left\{ {\begin{array}{*{20}{c}}{1 = \frac{{1 + 2 + a}}{3}}\\{c = \frac{{ - 3 - 4 - 2}}{3}}\\{3 = \frac{{3 + 5 + b}}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 0}\\{b = 1}\\{c =  - 3}\end{array}} \right.} \right.\)

Vậy \(a + b + c =  - 2\). Chọn D.

Ta có: \(f\left( x \right) = \frac{{{{\log }_2}x}}{x}\)

\( \Rightarrow f'\left( x \right) = \frac{{ - 1}}{{{x^2}}} \cdot {\log _2}x + \frac{1}{{x \cdot \ln 2}} \cdot \frac{1}{x} = \frac{{1 - {{\log }_2}x \cdot \ln 2}}{{{x^2} \cdot \ln 2}} = \frac{{1 - \ln x}}{{{x^2} \cdot \ln 2}}\). Chọn B.

Giả sử số phức \(z\) có dạng: \(z = x + yi\,\,\left( {x\,,\,\,y \in \mathbb{R}} \right)\)

Ta có: \(iz + (1 - i)\bar z =  - 2i \Leftrightarrow i\left( {x + yi} \right) + \left( {1 - i} \right)\left( {x - yi} \right) =  - 2i \Leftrightarrow x - 2y - yi =  - 2i.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 2y = 0}\\{ - y =  - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = 2}\end{array} \Rightarrow x + y = 6} \right.} \right..\)

Tổng phần thực và phần ảo của số phức \(z\) bằng 6. Chọn A.

Từ đồ thị ta có:

• TCĐ: \(x = 1 \Rightarrow \frac{{ - d}}{{{c_a}}} = 1 \Rightarrow \frac{d}{c} =  - 1 \Rightarrow d =  - c\);

• TCN: \(y =  - 1 \Rightarrow \frac{a}{c} =  - 1 \Rightarrow a =  - c\).

Đồ thị cắt trục hoành tại điểm: \(x = 2 \Rightarrow \frac{{ - b}}{a} = 2 \Rightarrow \frac{{ - b}}{{ - c}} = 2 \Rightarrow b = 2c\)

Vậy \(T = \frac{{a - 2b + 3d}}{c} = \frac{{ - c - 4c - 3c}}{c} =  - 8\). Chọn C.

Gọi thiết diện là hình chữ nhật \[ABCD\], tâm 2 đáy lần lượt là \(O\) và \(O',\,\,CD\) thuộc đáy chứa tâm \(O,\,\,{\rm{H}}\) là trung điểm \[CD.\]

Ta có: \(\left\{ \begin{array}{l}OH \bot CD\\OH \bot BC\end{array} \right.\)\( \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow d\left( {OO';\left( {ABCD} \right)} \right) = OH = 3\,\,\;{\rm{cm}}.\)

\( \Rightarrow HC = HD = \sqrt {O{C^2} - O{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4\,\;({\rm{cm)}}.\)

\( \Rightarrow AB = CD = 8\,\;{\rm{cm}}.\)

\( \Rightarrow {S_{ABCD}} = AB \cdot BC = 8 \cdot 7 = 56\;\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\) Chọn B.

Giao điểm của đồ thị hàm số đã cho với trục tung là \(B\left( {0\,;\,\,2{m^2} + 4} \right)\).

Phương trình hoành độ giao điểm của đồ thị đã cho với trục hoành là:

\({x^3} + \left( {{m^2} - 2} \right)x + 2{m^2} + 4 = 0 \Leftrightarrow \left( {x + 2} \right)\left( {{x^2} - 2x + {m^2} + 2} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 2}\\{{{\left( {x - 1} \right)}^2} + {m^2} + 1 = 0\quad (VN)}\end{array}} \right.\)

Giao điểm của đồ thị đã cho với trục hoành là \(A\left( { - 2\,;\,\,0} \right).\)

Diện tích tam giác ABC là: \(S = \frac{1}{2} \cdot OA \cdot OB = \frac{1}{2} \cdot 2 \cdot \left( {2{m^2} + 4} \right) = 8 \Rightarrow m =  \pm \sqrt 2 \).

Chọn D.

Đặt \(u = \tan x \Rightarrow du = \frac{1}{{{{\cos }^2}x}}dx = \left( {1 + {{\tan }^2}x} \right)dx \Rightarrow \frac{{du}}{{{u^2} + 1}} = dx.\)

Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow u = 0\\x = \frac{\pi }{4} \Rightarrow u = 1\end{array} \right.\).

Ta có: \(\int\limits_0^{\frac{\pi }{4}} {f\left( {\tan x} \right)dx}  = \int\limits_0^1 {\frac{{f\left( u \right)}}{{{u^2} + 1}}} \,{\rm{d}}u = \int\limits_0^1 {\frac{{f\left( x \right)}}{{{x^2} + 1}}} \,{\rm{d}}x \Rightarrow \int\limits_0^1 {\frac{{f\left( x \right)}}{{{x^2} + 1}}} \,{\rm{d}}x = 2\).

Do đó \[I = \int\limits_0^1 {f\left( x \right)} \,{\rm{d}}x = \int\limits_0^1 {\frac{{\left( {{x^2} + 1} \right)f\left( x \right)}}{{{x^2} + 1}}} \,{\rm{d}}x = \int\limits_0^1 {\frac{{{x^2}f\left( x \right)}}{{{x^2} + 1}}\,} dx + \int\limits_0^1 {\frac{{f\left( x \right)}}{{{x^2} + 1}}} \,\,dx = 2 + 2 = 4\].

Chọn C.

Gọi \(O = AC \cap BD.\) Ta có: \(\left\{ {\begin{array}{*{20}{c}}{DO \bot AC}\\{DO \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)}\end{array} \Rightarrow DO \bot \left( {SAC} \right)} \right..\)

\( \Rightarrow {\rm{SO}}\) là hình chiếu của \[SD\] lên mặt phẳng \(\left( {SAC} \right)\)\[ \Rightarrow \widehat {\left( {SD;\,\,\left( {SAC} \right)} \right)} = \widehat {\left( {S\,;\,SO} \right)} = \widehat {DSO} = \alpha .\]

• Xét \(\Delta SAD\) vuông tại \({\rm{A}}\) ta có: \(SD = \sqrt {3{a^2} + {a^2}}  = 2a\)

• Xét \(\Delta SOD\) vuông tại O, có \(SD = 2a,\,\,OD = \frac{{a\sqrt 2 }}{2}.\)

\( \Rightarrow \sin \alpha  = \sin \widehat {DSO} = \frac{{DO}}{{SD}} = \frac{{\sqrt 2 }}{4}.\) Chọn A.

Ta có \({x^2} - 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x =  - 1}\end{array}\,\,;\,\,} \right.\)

\(2{x^2} + 3x - 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x =  - \frac{5}{2}}\end{array}\,\,;\,\,} \right.\)\(4 - {x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2}\\{x =  - 2}\end{array}} \right.\).

Trục xét dấu:

Tập nghiệm của bất phương trình là \(S = \left[ { - \frac{5}{2}\,;\,\, - 2} \right) \cup \left[ { - 1\,;\,\,2} \right)\).

Tổng bình phương các nghiệm nguyên bất phương trình là: \({\left( { - 1} \right)^2} + {\left( 0 \right)^2} + {\left( 1 \right)^2} = 2\). Chọn B.

Ta tính được \(OA = 3\,;\,\,OB = 4\,;\,\,AB = 5.\)

Vì \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm của đường tròn nội tiếp tam giác \[OAB\] nên ta có:

\(OA \cdot \overrightarrow {IB}  + OB \cdot \overrightarrow {IA}  + AB \cdot \overrightarrow {IO}  = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3\left( {\frac{8}{3} - a} \right) + 4\left( {1 - a} \right) + 5\left( { - a} \right) = 0}\\{3\left( {\frac{4}{3} - b} \right) + 4\left( {2 - b} \right) + 5\left( { - b} \right) = 0}\\{3\left( {\frac{8}{3} - c} \right) + 4\left( { - 2 - c} \right) + 5\left( { - c} \right) = 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 1}\\{c = 0}\end{array}} \right.\).

Vậy \(I\left( {1\,;\,\,1\,;\,\,0} \right)\), suy ra \(a - b + c = 0.\) Chọn D.

Trừ từng vế các phương trình của hệ ta được:

\(3{x^2} - 3{y^2} = x - y \Leftrightarrow \left( {x - y} \right)\left( {3x + 3y - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - y = 0}\\{3x + 3y - 1 = 0}\end{array}} \right.\).

Kết hợp với hệ phương trình ta có:

\(\left[ \begin{array}{l}\left\{ {\begin{array}{*{20}{c}}{x = y}\\{{x^2} - 2{y^2} = 2x + y}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{c}}{3x + 3y - 1 = 0}\\{{x^2} - 2{y^2} = 2x + y}\end{array}} \right.\end{array} \right.\)\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{x = y}\\{{x^2} + 3x = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{y = \frac{{1 - 3x}}{3}}\\{9{x^2} - 3x + 5 = 0\,\,(VN)}\end{array}} \right.}\end{array}} \right.\]\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{l}}{x = 0}\\{y = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x =  - 3}\\{y =  - 3}\end{array}} \right.}\end{array}} \right.\).

Vậy hệ phương trình đã cho có 2 nghiệm \[\left( {0\,;\,\,0} \right),\,\,\left( { - 3\,;\,\, - 3} \right).\] Chọn B.

Ta có \[B\] di chuyển được 15 s thì đuổi kịp \[A\], khi đó \[A\] di chuyển được 25 s.

Quãng đường vật \[A\] đi được là \[\int\limits_0^{25} {\left( {\frac{1}{{100}}{t^2} + \frac{{13}}{{30}}t} \right)} \,\,dt = \frac{{375}}{2}\,\,(m).\]

Do đó vật \[B\] cũng đi được quãng đường \(\frac{{375}}{2}m.\)

Vận tốc của vật \[B\] là \[{v_B}\,\,(t) = at\,\,(\;{\rm{m}}/{\rm{s}})\].

Suy ra Quãng đường vật \[B\] đi được trong 15 s là:\(\int\limits_0^{15} {atdt}  = \left. {\frac{{a{t^2}}}{2}} \right|_0^{15} = \frac{{225a}}{2} = \frac{{375}}{2} \Leftrightarrow a = \frac{5}{3}\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right)\).

\( \Rightarrow \) Vận tốc của \[B\] tại thời điểm đuổi kịp \[A\] là \(v\left( {15} \right) = \frac{5}{3} \cdot 15 = 25\,\,(\;{\rm{m}}/{\rm{s}})\). Chọn D.

Theo công thức tính tỉ lệ đã cho thì cần tìm nghiệm \(t\) của bất phương trình:

\(M\left( t \right) = 75 - 20\ln \left( {t + 1} \right) \le 10 \Leftrightarrow \ln \left( {t + 1} \right) \ge 3,25 \Rightarrow t \ge 24,79\).

Vậy sau khoảng 25 tháng thì học sinh nhớ được danh sách đó là dưới \[10\% .\] Chọn A.

Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) nằm trên đường thẳng \(\Delta :x - y - 2 = 0 \Rightarrow M\left( {x\,;\,\,x - 2} \right).\)

Khi đó: \[\overrightarrow {AM} \,\left( {x - 1\,;\,\,x - 3} \right);\,\,\overrightarrow {BM} \left( {x - 3\,;\,\,x - 4} \right)\].

Tam giác MAB vuông tại \[M \Leftrightarrow \overrightarrow {AM}  \cdot \overrightarrow {BM}  = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 3} \right) + \left( {x - 3} \right)\left( {x - 4} \right) = 0\]

\( \Leftrightarrow \left( {x - 3} \right)\left( {x - 1 - x + 4} \right) = 0 \Rightarrow x = 3 \Rightarrow y = x - 2 = 1 \Rightarrow T = x + 3y = 3 + 3 = 6\).

Chọn D.

Vì \(\sin \left[ {\frac{\pi }{{178}}} \right]\left( {t - 60} \right) \le 1 \Rightarrow t = y = 4\sin \left[ {\frac{\pi }{{178}}} \right]\left( {t - 60} \right) + 10 \le 14.{\rm{ }}\)

Ngày có ánh sáng mặt trời nhiều nhất \( \Leftrightarrow y = 14 \Leftrightarrow \sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] = 1\)

\( \Leftrightarrow \frac{\pi }{{178}}\left( {t - 60} \right) = \frac{\pi }{2} + k2\pi  \Leftrightarrow t = 149 + 356k\)Do \(0 < t \le 365 \Rightarrow 0 < 149 + 356k \le 365 \Leftrightarrow  - \frac{{149}}{{356}} < k \le \frac{{54}}{{89}}\), mà \(k \in \mathbb{Z}\) nên \(k = 0.\)

Với \(k = 0 \Rightarrow t = 149\) rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện \(0 < t \le 365\) thì ta biết năm nay tháng 2 chỉ có 28 ngày).

Chọn B.

Gọi \(O = AC \cap BD.\)

Ta có \(AO \bot BD \Rightarrow SO \bot BD\)

 Suy ra  \(\left( {\widehat {\left( {{\rm{SBD}}} \right),\,\,\left( {{\rm{ABCD}}} \right)}} \right) = \widehat {SOA} = 60^\circ \).

\({V_{S.ADN}} = \frac{1}{2} \cdot {V_{S \cdot ADC}} = \frac{1}{4} \cdot {V_{S.ABCD}}\) và

 \({V_{S.AMN}} = \frac{1}{2} \cdot \frac{1}{2}{V_{S.ABC}} = \frac{1}{8}{V_{S.ABCD.}}\)

Ta có: \(y' = 3{x^2} - 2mx + 12\)

Yêu cầu bài toán \( \Leftrightarrow y' \ge 0;\forall x \in \left( {1\,;\, + \infty } \right)\)

\( \Leftrightarrow 3{x^2} + 12 \ge 2mx\,;\,\,\forall x \in \left( {1\,;\, + \infty } \right) \Leftrightarrow \frac{{3{x^2} + 12}}{{2x}} \ge m;\,\,\forall x \in \left( {1\,;\, + \infty } \right)\)

Xét hàm \(h\left( x \right) = \frac{{3{x^2} + 12}}{{2x}} = \frac{{3x}}{2} + \frac{6}{x}\) có \(h'\left( x \right) = \frac{3}{2} - \frac{6}{{{x^2}}} = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x =  \pm 2\).

Ta có BBT của \(h\left( x \right)\) trên \(\left( {1\,;\, + \infty } \right)\).

Đặt \(t = \sqrt {x + 1}  > 1 \Rightarrow {t^2} = x + 1 \Rightarrow x = {t^2} - 1\)

\[ \Rightarrow f'\left( x \right) = \frac{{{t^2} - 1}}{{{t^2} - t}} = \frac{{\left( {t - 1} \right)\left( {t + 1} \right)}}{{\left( {t - 1} \right)t}} = \frac{{t + 1}}{t} = 1 + \frac{1}{t} = \frac{1}{{\sqrt {x + 1} }} + 1\]

\( \Rightarrow f\left( x \right) = \int {f'\left( x \right)} \,\,dx = \int {\left( {1 + \frac{1}{{\sqrt {x + 1} }}} \right)} \,\,{\rm{d}}x = x + \int {\frac{{{\rm{d}}\left( {x + 1} \right)}}{{\sqrt {x + 1} }}} \)\[ = x + 2\int {\frac{{{\rm{d}}\left( {x + 1} \right)}}{{2\sqrt {x + 1} }}}  = x + 2\sqrt {x + 1}  + C\].

Mà \(f\left( 3 \right) = 3 \Rightarrow 3 + 2 \cdot \sqrt {3 + 1}  + C = 3 \Rightarrow C =  - 4 \Rightarrow f\left( x \right) = x + 2\sqrt {x + 1}  - 4\).

Suy ra \[\int\limits_3^8 {f\left( x \right)} \,{\rm{d}}x = \int\limits_3^8 {\left( {x + 2\sqrt {x + 1}  - 4} \right)} \,{\rm{d}}x = \frac{{197}}{6}\]. Chọn B.

Đặt \(AB = x.\) Gọi \({\rm{M}}\) là trung điểm \({\rm{BC}}.\)

Ta có \(\left\{ {\begin{array}{*{20}{c}}{\left( {A'BC} \right) = \left( {ABC} \right) = BC}\\{AM \bot BC}\\{A'M \bot BC}\end{array}} \right.\)

Gọi hình chiếu vuông góc của điểm \[I\] lên đoạn thẳng \[MN\] là \[K.\]

Dễ thấy: \(AN = NK = \frac{1}{3}AM\), mặt cầu \(\left( S \right)\) có tâm \(I\left( {1\,;\,\,2\,;\,\,3} \right)\) và bán kính \(R = 5.\)

Có \(AM \cdot AN = A{I^2} - {R^2} = 4 \Rightarrow A{N^2} = \frac{4}{3}\)

Đồ thị hàm số \(y = \left| {{x^4} - 2m{x^2} + 25} \right|\) có 7 điểm cực trị khi và chỉ khi \(f\left( x \right) = {x^4} - 2m{x^2} + 25\) có 3 cực trị và giá trị cực tiểu nhỏ hơn 0.

\(f'\left( x \right) = 4{x^3} - 4xm = 4x\left( {{x^2} - m} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = m}\end{array}} \right.\).

Yêu cầu bài toán tương đương \(\left[ {\begin{array}{*{20}{l}}{m > 0}\\{f( \pm m) < 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 0}\\{{m^2} - 2m.m + 25 > 0}\end{array} \Rightarrow m \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4} \right\}} \right.} \right.\).

Do đó \(S = 1 + 2 + 3 + 4 = 10\). Chọn B.

Điều kiện: \(x > 0\).

Ta có \({\log _2}\left( {2x} \right) \cdot \log \left( {\frac{{100}}{x}} \right) > 2\)\( \Leftrightarrow \left( {1 + {{\log }_2}x} \right)\left( {2 - \log x} \right) > 2\)

\( \Leftrightarrow 2 - \log x + 2{\log _2}x - \log x \cdot {\log _2}x > 2\)\( \Leftrightarrow 2{\log _2}x - \log 2 \cdot {\log _2}x - \log x \cdot {\log _2}x > 0\)

\[ \Leftrightarrow {\log _2}x\left( {2 - \log 2 - \log x} \right) > 0 \Leftrightarrow {\log _2}x\left( {\log 50 - \log x} \right) > 0\]

\( \Leftrightarrow \left[ {\left\{ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{{{\log }_2}x > 0}\\{\log 50 - \log x > 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{{{\log }_2}x < 0}\\{\log 50 - \log x < 0}\end{array}} \right.}\end{array}} \right.} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x > 1}\\{x < 50}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x < 1}\\{x > 50}\end{array}} \right.}\end{array} \Leftrightarrow 1 < x < 50} \right.\).

Vậy có 48 số nguyên thỏa mãn. Chọn B.

Tập xác định: \(D = \mathbb{R}\backslash \{ m\} \). Để hàm số có giá trị lớn nhất trên \[\left[ {1\,;\,\,3} \right]\] thì \(m \notin \left[ {1\,;\,\,3} \right].\)

Ta có \(y' = \frac{{ - 2m - 6}}{{{{\left( {x - m} \right)}^2}}}\).

• Trường hợp 1: \( - 2m - 6 > 0 \Leftrightarrow m <  - 3\).

Khi đó \({\max _{x \in \left[ {1\,;\,\,3} \right]}}y = y\left( 3 \right) = \frac{{m + 9}}{{3 - m}}\).

Để giá trị lớn nhất trên đoạn \[\left[ {1\,;\,\,3} \right]\] là số dương thì \(\frac{{m + 9}}{{3 - m}} > 0 \Leftrightarrow m + 9 > 0 \Leftrightarrow m >  - 9\)

Vậy các số nguyên \(m\) thỏa là \( - 8\, & ;\,\, - 7\, & ;\,\, - 6\, & ;\,\, - 5\, & ;\,\, - 4.\)

• Trường hợp 2: \( - 2m - 6 < 0 \Leftrightarrow m >  - 3\).

Khi đó \[{\max _{x \in \left[ {1\,;\,\,3} \right]}}y = y(1) = \frac{{m + 7}}{{1 - m}}\].

Để giá trị lớn nhất trên đoạn \[\left[ {1\,;\,\,3} \right]\] là số dương thì \(\frac{{m + 7}}{{1 - m}} > 0 \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1\)

Vậy các số nguyên thỏa mãn là \( - 2\,;\,\, - 1\,;\,0\).

• Trường hợp 3: \( - 2m - 6 = 0 \Leftrightarrow m =  - 3\).

Khi đó \(y = 1\) nên \({\max _{x \in \left[ {1\,;\,\,3} \right]}}y = 1\).

Vậy \(m =  - 3\) thỏa mãn.

Ta có \(\left( {{P_m}} \right):mx + 2y + nz + 1 = 0\) có vectơ pháp tuyến \(\overrightarrow {{n_1}} \left( {m\,;\,2\,;\,n} \right).\)

\(\left( {{Q_m}} \right):x + my + nz + 2 = 0\) có vectơ pháp tuyến \(\overrightarrow {{n_2}} \left( {1\,;\, - m\,;\,n} \right)\).

\((\alpha ):4x - y - 6z + 3 = 0\) có vectơ pháp tuyến \(\overrightarrow {{n_\alpha }} \left( {4\,;\, - 1\,;\, - 6} \right)\).

Giao tuyến của hai mặt phẳng \(\left( {{P_m}} \right)\) và \(\left( {{Q_m}} \right)\) vuông góc với mặt phẳng \((\alpha )\) nên ta có hệ phương trình: \(\left\{ \begin{array}{l}({P_m}) \bot (\alpha )\\({Q_m}) \bot (\alpha )\end{array} \right.\)\[ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_1}}  \bot \overrightarrow {{n_\alpha }} \\\overrightarrow {{n_2}}  \bot \overrightarrow {{n_\alpha }} \end{array} \right.\]\( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_1}}  \cdot \overrightarrow {{n_\alpha }}  = 0\\\overrightarrow {{n_2}}  \cdot \overrightarrow {{n_\alpha }}  = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}4m - 2 - 6n = 0\\4 + m - 6n = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = 2\\n = 1\end{array} \right.\).

Vậy \(m + n = 3\). Chọn D.

Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị.

Khi đó, phương trình các parabol mới là \(\left( {{P_1}} \right):y =  - {x^2} + 4,\,\,\left( {{P_2}} \right):y =  - \frac{a}{4}{x^2} + a.\)

Gọi \[A,\,\,B\] là các giao điểm của \(\left( {{P_1}} \right)\) và trục \(Ox \Rightarrow A\left( { - 2\,;\,\,0} \right),B\left( {2\,;\,\,0} \right) \Rightarrow AB = 4.\)

Gọi \[M,\,\,N\] là các giao điểm của \(\left( {{P_1}} \right)\) và đường thẳng \(d \Rightarrow M\left( { - \sqrt {4 - a} \,;\,a} \right),N\left( {\sqrt {4 - a} ;\,\,a} \right).\)

Ta có: \({S_1} = 2\int\limits_\alpha ^4 {\sqrt {4 - y} } dy =  - \left. {\frac{4}{3}\left( {{{\left( {4 - y} \right)}^{\frac{3}{2}}}} \right)} \right|_\alpha ^4 = \frac{4}{3}\left( {4 - a} \right)\sqrt {4 - a} \);

\[{S_2} = 2\int\limits_\alpha ^2 {\left( { - \frac{a}{4}{x^2} + a} \right)} \,dx = \left. {2\left( { - \frac{{a{x^3}}}{{12}} + ax} \right)} \right|_0^2 = \frac{{8a}}{3}\].

Theo giả thiết \({S_1} = {S_2} \Rightarrow \frac{4}{3}\left( {4 - a} \right)\sqrt {4 - a}  = \frac{{8a}}{3} \Leftrightarrow \left( {4 - {a^3}} \right) = 4{a^2} \Leftrightarrow {a^3} - 8{a^2} + 48a = 64\)

Vậy \(T = 64.\) Chọn B.

Điều kiện \(m \ne 0.\)

Phương trình tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là \(x + 2 = 0\) và \(y - 1 = 0.\)

Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng \(m - 2\) là:

\(\left( d \right):y = \frac{{3x}}{{{m^2}}} + \frac{{{m^2} - 6m + 6}}{{{m^2}}}.\)

Đường thẳng \(d\) cắt tiệm cận đứng của đồ thị hàm số tại điểm \(A\left( { - 2\,;\,\,\frac{{m - 6}}{m}} \right)\) và cắt tiệm cận ngang của đồ thị hàm số tại điểm \(B\left( {2m - 2\,;\,\,1} \right)\).

Theo giả thiết ta có \[2m - 2 + \frac{{m - 6}}{m} =  - 5 \Rightarrow m = 1\,;\,\,m =  - 3\]

Vậy bằng tổng bình phương các phần tử của \(S\) bằng 10. Chọn A.

Ta có: \(\frac{{{V_{D.APN}}}}{{{V_{D.ABC}}}} = \frac{{DP}}{{DB}} \cdot \frac{{DN}}{{DC}} = \frac{1}{4};\)

\(\frac{{{V_{B.APM}}}}{{{V_{B.ACD}}}} = \frac{{BP}}{{BD}} \cdot \frac{{BM}}{{BC}} = \frac{1}{4};\frac{{{V_{C.AMN}}}}{{{V_{C.ABD}}}} = \frac{{CM}}{{CB}} \cdot \frac{{CN}}{{CD}} = \frac{1}{4}.\)

Mà: \({V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} - {V_{BAPM}} - {V_{CAMN}} = \frac{1}{4}{V_{ABCD}}\)

Gọi \(I\) là điểm thỏa \(\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC}  = \vec 0 \Leftrightarrow I\left( {2\,;\,\, - 2\,;\,\,2} \right)\)

\(M{A^2} + M{B^2} + M{C^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI}  + \overrightarrow {IC} } \right)^2}\)

\( = 3M{I^2} + I{A^2} + I{B^2} + I{C^2} + 2\overrightarrow {MI}  \cdot \left( {\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC} } \right) = 3M{I^2} + I{A^2} + I{B^2} + I{C^2}\).

Mà \(M \in Oxyz \Rightarrow M{A^2} + M{B^2} + M{C^2}\) đạt giá trị nhỏ nhất

\( \Leftrightarrow M\) là hình chiếu của \(I\) lên \[\left( {Oyz} \right) \Leftrightarrow M\left( {0\,;\,\, - 2\,;\,\,2} \right).\]

Vậy \(P = 0 - 2 + 2 = 0\). Chọn A.

Ta có: \[g'\left( x \right) =  - 2f'\left( {1 - 2x} \right) + 2x - 1 =  - 2\left[ {f'(1 - 2x) - \frac{{\left( {1 - 2x} \right)}}{2}} \right]\].

Từ đồ thị trên suy ra \(g'\left( x \right) \le 0 \Leftrightarrow f'\left( {1 - 2x} \right) - \frac{{\left( {1 - 2x} \right)}}{2} \Leftrightarrow \left( {1 - 2x} \right) \in \left[ { - 2\,;\,\,0} \right] \cup \left[ {4\,;\,\, + \infty } \right)\)

\( \Rightarrow 2x \in \left( { - \infty \,;\,\, - 3} \right] \cup \left[ {1\,;\,\,3} \right] \Rightarrow x \in \left( { - \infty ;\, - \frac{3}{2}} \right] \cup \left[ {\frac{1}{2};\frac{3}{2}} \right]\). Chọn A.

Theo bài ta có \({h_n} = 4{h_1} \Rightarrow {h_1} = \frac{1}{4}{h_n};{h_2} = 2{h_1} = \frac{1}{2}{h_n}\).

Thể tích toàn bộ con xoay là:

\[V = {V_{\left( {T1} \right)}} + {V_{\left( {T2} \right)}} + {V_{\left( N \right)}} = \pi  \cdot r{ \cdot ^2}{h_1} + \pi  \cdot {\left( {2r} \right)^2} \cdot {h_2} + \frac{1}{3}\pi  \cdot {r^2} \cdot {h_n}\]

\( \Leftrightarrow \pi  \cdot {r^2} \cdot \frac{1}{4}{h_n} + \pi  \cdot 4{r^2} \cdot \frac{1}{2}{h_n} + \frac{1}{3}\pi  \cdot {r^2} \cdot {h_n} \Leftrightarrow 31 = \frac{3}{4}\left( {\frac{1}{3}\pi  \cdot {r^2} \cdot {h_n}} \right) + 6\left( {\frac{1}{3}\pi  \cdot {r^2} \cdot {h_n}} \right)\)

\( \Leftrightarrow \frac{1}{3}\pi  \cdot {r^2} \cdot {h_n} \Leftrightarrow 31 = \frac{{31}}{4}\,\,\,\left( {\frac{1}{3}\pi  \cdot {r^2} \cdot {h_n} = 4} \right)\).

Vậy thể tích khối nón \(\left( N \right)\) là: \({V_{\left( N \right)}} = 4\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right)\). Chọn C.

Gọi số phần quà Sử - Địa là \[xx\], số phần quà Sử - GDCD là \[yy\] và số phần quà Địa - GDCD là \[zz.\]

Tổng số phần quà là 15 nên \(x + y + z = 15.\)

Phần quà có môn sử có 2 kiểu: Sử - Địa (\(x\) phần quà) và Sử - GDCD (\(y\) phần quà).

Do có 12 quyển sách sử nên 12 quyển này nằm hoàn toàn trong 2 kiểu phần quà trên.

Do đó: \(x + y = 12\).

Tương tự, ta có: Địa: \(z + x = 8;\) GDCD: \(y + z = 10.\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x + y + z = 15}\\{x + y = 12}\\{y + z = 10}\\{x + z = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 5}\\{y = 7}\\{z = 3}\end{array}} \right.} \right.\).

Suy ra số phần quà Sử - Địa là 5; Sử - GDCD là 7; Địa - GDCD là 3.

Chọn 2 trong 15 phần quà \( \Rightarrow \) Không gian mẫu \(n\left( \Omega  \right) = C_{15}^2 = 105\).

Gọi A là biến cố: "Hai phần quà lấy được khác nhau", khi đó ta có:

\(n\left( A \right) = C_5^1 \cdot C_7^1 + C_7^1 \cdot C_3^1 + C_3^1 \cdot C_5^1 = 71\).

Vậy \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( P \right)}} = \frac{{71}}{{105}}.\] Chọn B.

Ta có \({u_{n + 1}} = \frac{{\left( {n + 2} \right){u_n} + 2}}{n} \Leftrightarrow n{u_{n + 1}} = \left( {n + 2} \right){u_n} + 2\,\,\forall n \in \mathbb{N}*\).

Đặt \({u_n} = {v_n} - 1,\,\,\forall n \in \mathbb{N}*\) thì \({v_1} = 1 + 1 = 2\) và \(n{u_{n + 1}} = \left( {n + 2} \right){u_n} + 2\).

Do đó \(n{v_{n + 1}} = \left( {n + 2} \right){v_n} \Leftrightarrow \frac{{{v_{n + 1}}}}{{\left( {n + 1} \right)\left( {n + 2} \right)}} = \frac{{{v_n}}}{{n\left( {n + 1} \right)}} \Rightarrow \frac{{{v_1}}}{2} = 1\)

\( \Rightarrow {v_n} = n\left( {n + 1} \right) \Rightarrow {u_n} = n\left( {n + 1} \right) - 1 = {n^2} + n - 1\).

Vậy \(\lim \frac{{{u_n}}}{{{n^2}}} = \lim \frac{{{n^2} + n - 1}}{{{n^2}}} = 1\).

Đáp án: 1.

Ta có: \({V_{{N_1}}} = \frac{1}{3}\pi {R^2} \cdot SO,\,\,{V_{{N_2}}} = \frac{1}{3}\pi {R^2} \cdot SO'\)

Mặt khác, \(\Delta SO'A\) và \(\Delta SOB\) đồng dạng nên \(\frac{{R'}}{R} = \frac{{SO'}}{{SO}}\).

Suy ra: \(\frac{{{V_{{N_2}}}}}{{{V_{{N_1}}}}} = \frac{{{{R'}^2} \cdot SO'}}{{{R^2} \cdot SO}} = {\left( {\frac{{SO'}}{{SO}}} \right)^3} = \frac{1}{8}\).

Do đó \(\frac{{SO'}}{{SO}} = \frac{1}{2} \Rightarrow SO' = \frac{1}{2} \cdot 40 = 20\;\,({\rm{cm)}}.\)

Ta có \[f'\left( x \right) = 0 \Leftrightarrow \left( {{x^2} - 1} \right)\left( {\ln x - 2} \right) = 0\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = {e^2}}\end{array}} \right.\] (loại \(x =  - 1\) vì vi phạm điều kiện của \(\left. {\ln x} \right)\)

Ta thấy đây là nghiệm đơn và \[f'\left( x \right)\] chỉ đổi dấu qua 2 nghiệm này.

Như vậy hàm số đã cho có 2 điểm cực trị. Đáp án: 2.

Độ dài cạnh đáy \[AB\] là \(a\,(m)\), độ dài cạnh còn lại BC là \(9 - a\,\,(m)\), chiều cao \(AA'\) là \(a\,(m).\)

Thể tích của khối hộp chữ nhật là: \(V = a\left( {9 - a} \right) \cdot a = 9{a^2} - {a^3}\,\left( {{m^3}} \right)\).

Ta có: \(V' = 18a - 3{a^2} = 0 \Rightarrow a = 6\).

Dễ thấy đồ thị có 1 đường TCN: \(y = 0\).

Yêu cầu bài toán \( \Leftrightarrow {x^2} - 8x + m = 0\) có 2 nghiệm phân biệt khác 1 \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 - 8 + m \ne 0}\\{{4^2} - m > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ne 7}\\{m < 16}\end{array}} \right.} \right.\)

Suy ra có 14 giá trị nguyên của \(m\) thỏa mãn. Đáp án: 14.

\({\log _{2 + \sqrt 5 }}\left( {2{x^2} - x - 4{m^2} + 2m} \right) + {\log _{\sqrt {\sqrt 5  - 2} }}\sqrt {{x^2} + mx - 2{m^2}}  = 0\)

\( \Leftrightarrow {\log _{2 + \sqrt 5 }}\left( {2{x^2} - x - 4{m^2} + 2m} \right) + {\log _{\sqrt 5  - 2}}\left( {{x^2} + mx - 2{m^2}} \right) = 0\)

\( \Leftrightarrow {\log _{2 + \sqrt 5 }}\left( {2{x^2} - x - 4{m^2} + 2m} \right) + {\log _{\frac{{5 - 4}}{{\sqrt 5  + 2}}}}\left( {{x^2} + mx - 2{m^2}} \right) = 0\)

\( \Leftrightarrow {\log _{2 + \sqrt 5 }}\left( {2{x^2} - x - 4{m^2} + 2m} \right) - {\log _{\sqrt 5  + 2}}\left( {{x^2} + mx - 2{m^2}} \right) = 0\)

\( \Leftrightarrow {\log _{2 + \sqrt 5 }}\left( {\frac{{2{x^2} - x - 4{m^2} + 2m}}{{{x^2} + mx - 2{m^2}}}} \right) = 0\)\( \Leftrightarrow \frac{{2{x^2} - x - 4{m^2} + 2m}}{{{x^2} + mx - 2{m^2}}} = 1\)

\( \Leftrightarrow {x^2} - (1 + m)x - 2{m^2} + 2m = 0\)

Yêu cầu bài toán \( \Leftrightarrow \left\{ \begin{array}{l}{(1 + m)^2} + 2{m^2} - 2m > 0\\{x_1}^2 + {x_2}^2 = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3{m^2} + 1 > 0\\{\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 3\end{array} \right.\)

\( \Rightarrow {\left( {1 + m} \right)^2} - 2\left( {2m - 2{m^2}} \right) = 3 \Leftrightarrow {m^2} + 2m + 1 - 4m + 4{m^2} = 3 \Leftrightarrow 5{m^2} - 2m - 2 = 0\)

\( \Leftrightarrow m = \frac{{1 \pm \sqrt {11} }}{5}\).

Suy ra không có giá trị nguyên nào của \(m\) thỏa mãn yêu cầu bài toán. Đáp án: 0.

Gọi \(M\left( {a;\,\,b} \right)\) là điểm biểu diễn số phức \(z = a + bi\)

\(A\left( {1;\,\,2} \right)\) là điểm biểu diễn số phức \(1 + 2i\)

\(B\left( { - 2;\,\,3} \right)\) là điểm biểu diễn số phức \( - 2 + 3i\,;\,\,AB = \sqrt {10} \)

\(\left| {z - 1 - 2i} \right| + \left| {z + 2 - 3i} \right| = \sqrt {10} \) trở thành \(MA + MB = AB\)

Ta có \[\int\limits_0^2 {\left[ {f\left( {1 - 3x} \right) + 9} \right]} \,dx = \int\limits_0^2 {f\left( {1 - 3x} \right)} \,dx + \int\limits_0^2 9 \,dx = \int\limits_0^2 {f\left( {1 - 3x} \right)} \,dx + 18\]

Xét \[\int\limits_0^2 {f\left( {1 - 3x} \right)} \,dx\], đặt \(t = 1 - 3x \Rightarrow dt =  - 3dx \Rightarrow dx =  - \frac{{dt}}{3}.\)

Đổi cận khi \(x = 0 \Rightarrow t = 1\,;\,\,x = 2 \Rightarrow t =  - 5.\)

Suy ra \[\int\limits_0^2 {f\left( {1 - 3x} \right)\,} dx =  - \frac{1}{3}\int\limits_1^{ - 5} {f\left( t \right)\,} dt = \frac{1}{3}\int\limits_{ - 5}^1 {f\left( t \right)\,} dt\].

Khi đó \[\int\limits_0^2 {\left[ {f\left( {1 - 3x} \right) + 9} \right]} \,dx = \frac{1}{3}\int\limits_{ - 5}^1 {f\left( t \right)\,} dt + 18 = \frac{1}{3}\int\limits_{ - 5}^1 {f\left( x \right)\,} dx + 18 = 21\]. Đáp án: 21.

Gọi \(x\) (nghìn đồng) là giá phòng khách sạn \((x > 400).\)

Giá chênh lệch sau khi tăng là: \(x - 400\) (nghìn đồng).

Số phòng trống lúc này là: \(2 \cdot \frac{{x - 400}}{{20}} = \frac{{x - 400}}{{10}}\) (phòng).

Số phòng cho thuê lúc này là: \(50 - \frac{{x - {{400}^{10}}}}{{20}} = \frac{{900 - x}}{{10}}\) (phòng).

Số tiền phòng thu được là: \(f\left( x \right) = x \cdot \left( {\frac{{900 - x}}{{10}}} \right) = \frac{{ - {x^2} + 900x}}{{10}}\) (nghìn đồng).

Ta cần tìm \(x > 400\) sao cho \(f\left( x \right)\) đạt giá trị lớn nhất.

Dễ thấy \(x =  - \frac{{900}}{{2 \cdot ( - 1)}} = 450\) thì lớn nhất. Đáp án: 450.

Điều kiện \(m + 1 \ge 0 \Leftrightarrow m \ge  - 1 \cdot \Delta  = {m^2} - 4m - 5\).

• Trường hợp 1: \(\Delta  \ge 0 \Leftrightarrow {m^2} - 4m - 5 \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 5}\\{m \le 1}\end{array}} \right.\) phương trình có 2 nghiệm thực \({z_1},\,\,{z_2}.\)

Theo định lý Viète, ta có: \({z_1}.{z_2} =  - \frac{1}{4}\left( {{m^2} - 5m - 6} \right)\)

\(\left| {{z_1} + {z_2}} \right| \le \left| {{z_1} - {z_2}} \right| \Leftrightarrow {\left| {{z_1} + {z_2}} \right|^2} \le {\left| {{z_1} - {z_2}} \right|^2} \Leftrightarrow 4{z_1} \cdot {z_2} \le 0\)

\( - \left( {{m^2} - 5m - 6} \right) \le 0 \Leftrightarrow {m^2} - 5m - 6 \ge 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m \ge 6}\\{m \le  - 1}\end{array}} \right.\).

Do \(m \in \mathbb{Z}\) và \(m \in \left[ { - 10\,;\,\,10} \right]\) nên số giá trị \(m\) thỏa mãn \(\left( {10 - 6} \right) + 1 + 1 = 6.\)

• Trường hợp 2: \(\Delta  < 0 \Leftrightarrow {m^2} - 4m - 5 < 0 \Leftrightarrow  - 1 < m < 5\) phương trình có 2 nghiệm phức \({z_1},{z_2}.\)

\(\left| {{z_1} + {z_2}} \right| \le \left| {{z_1} - {z_2}} \right| \Leftrightarrow {\left| {{z_1} + {z_2}} \right|^2} \le {\left| {{z_1} - {z_2}} \right|^2} \Leftrightarrow m + 1 \le \left| {{m^2} - 4m - 5} \right|\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5m - 6 \ge 0}\\{{m^2} - 3m - 4 \le 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m \ge 6}\\{m \le  - 1}\\{ - 1 \le m \le 4}\end{array}} \right.} \right.\).

Do \(m \in \mathbb{Z}\,,\)\(m < 5\) và \(m \in \left[ { - 10\,;\,\,10} \right]\) nên số giá trị \(m\) thỏa mãn là \(m = 0\,;\,\,m = 1\,;\,\,m = 2\,;\,\,m = 3.\)

Vậy có 10 giá trị của \(m\) thoả mãn yêu cầu bài toán. Đáp án: 10.

Gọi \(\left( Q \right),\,\,\left( R \right)\) lần lượt là hai mặt phẳng chứa \(d\,,\,\,\Delta \) và vuông góc với \(\left( P \right)\).

Khi đó, \(M = \left( P \right) \cap \left( Q \right) \cup \left( R \right)\)

Mặt phẳng \(\left( P \right)\) có VTPT \(\vec n = \left( {1\,;\,\,1\,;\,\, - 1} \right)\)

Đường thẳng \(d\) có VTPT \(\overrightarrow {{u_1}}  = \left( {0\,;\,\,1\,;\,\,2} \right)\) và đi qua điểm \(M( - 2;0;2)\)

Mặt phẳng \(\left( Q \right)\) có VTPT \(\overrightarrow {{n_1}}  = \left[ {\overrightarrow {{u_1}} \,;\,\,\vec n} \right] = \left( { - 3\,;\,\,2\,;\,\, - 1} \right)\)

\( \Rightarrow \left( Q \right):3\left( {x + 2} \right) - 2\left( {y - 0} \right) + z - 2 = 0 \Leftrightarrow 3x - 2y + z + 4 = 0\)

Đường thẳng \(\Delta \) có VTPT \[\overrightarrow {{u_2}}  = \left[ {1\,;\, - 1\,;\, - 1} \right]\] và đi qua điểm \(M(3;1;4)\)

Mặt phẳng \((R)\) có VTPT \(\overrightarrow {{n_2}}  = \left[ {\overrightarrow {{u_2}} \,;\,\vec n} \right] = \left( {0\,;\,2\,;\,2} \right)\)

\( \Rightarrow (R):0(x - 3) + 1(y - 1) + 1(z - 4) = 0 \Leftrightarrow y + z - 5 = 0\)

Tọa độ điểm \(M\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x + y - z =  - 2}\\{3x - 2y + z =  - 4}\\{y + z = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x =  - 1}\\{y = 2}\\{z = 3}\end{array} \Rightarrow M\left( { - 1\,;\,\,2\,;\,\,3} \right) \Rightarrow a + bc = 5} \right.} \right..\)

Đáp án: 5.

Giả sử số tự nhiên chẵn có 6 chữ số là \(\overline {abcdef} \).

Chọn hệ trục tọa độ \[Oxyz\] sao cho gốc tọa độ \(O \equiv A',\,\,Ox \equiv A'D',\,\,Oy \equiv A'B',\,\,Oz \equiv A'A.\)

Khi đó: \(A'\left( {0\,;\,\,0\,;\,\,0} \right),\,\,D'\left( {a\,;\,\,0\,;\,\,0} \right),\,\,B'\left( {0\,;\,\,a\,;\,\,0} \right),\,\,C'\left( {a\,;\,\,a\,;\,\,0} \right),\)

\(A\left( {0\,;\,\,0\,;\,\,a} \right),\,\,D\left( {a\,;\,\,0\,;\,\,a} \right),\,\,B\left( {0\,;\,\,a\,;\,\,a} \right),\,\,C\left( {a\,;\,\,a\,;\,\,a} \right)\)

\[ \Rightarrow \overrightarrow {A'B'}  = \left( {0\,;\,\,a\,;\,\,0} \right),\,\,\overrightarrow {A'D}  = (a\,;\,\,0\,;\,\,a),\]\[\,\,\overrightarrow {A'A}  = \left( {0\,;\,\,0\,;\,\,a} \right),\,\,\overrightarrow {A'C'}  = \left( {a\,;\,\,a\,;\,\,0} \right).\]

Ta có: \(x + \sqrt {{x^2} + 2020}  > x + \left| x \right| \ge 0 \Rightarrow x + \sqrt {{x^2} + 2020}  > 0,\,\,\forall x \in \mathbb{R}.\)

Từ giả thiết: \[{2020^{f\left( x \right)}} = x + \sqrt {{x^2} + 2020}  \Leftrightarrow f\left( x \right) = {\log _{2020}}\left( {x + \sqrt {{x^2} + 2020} } \right).\]

\({2020^{f\left( x \right)}} = x + \sqrt {{x^2} + 2020}  \Leftrightarrow f\left( x \right) = {\log _{2020}}\left( {x + \sqrt {{x^2} + 2020} } \right){\rm{. }}\)

Ta có: \(f'\left( x \right) = \frac{{1 + \frac{x}{{\sqrt {{x^2} + 2020} }}}}{{\left( {x + \sqrt {{x^2} + 2020} } \right)\ln 2020}} = \frac{{x + \sqrt {{x^2} + 2020} }}{{\left( {x + \sqrt {{x^2} + 2020} } \right)\ln 2020\sqrt {{x^2} + 2020} }} > 0,\,\,\forall x \in \mathbb{R}\)

Suy ra hàm số \(f(x)\) luôn đồng biến trên \(\mathbb{R}.\)

Mà với \(\left\{ {\begin{array}{*{20}{l}}{m > 0}\\{m \ne 1}\end{array}} \right.\) thì \(f\left( {\log m} \right) < f\left( {{{\log }_m}2020} \right) \Leftrightarrow \log m < {\log _m}2020\).

Kết hợp với \(\left\{ {\begin{array}{*{20}{l}}{m > 0}\\{m \ne 1}\end{array}} \right.\) và \(m \in \mathbb{Z}\) nên \(m \in \left\{ {2\,;\,\,3\,;\,\, \ldots \,;\,\,65} \right\}\).

Vậy có tất cả 64 giá trị nguyên \(m\) thỏa mãn yêu cầu bài toán. Đáp án: 64.

Các từ “thỏ thẻ”, “rì rầm”, “lao xao” là các từ tượng thanh còn “thất thểu” là từ tượng hình. Chọn A.

Các tác phẩm A, B, D thuộc thể loại truyện ngắn. C thuộc loại tùy bút. Chọn C.

Tác phẩm “Sóng” là cuộc hành trình khởi đầu là sự từ bỏ cái chật chội, nhỏ hẹp để tìm đến một tình yêu bao la rộng lớn, cuối cùng là khát vọng được sống hết mình trong tình yêu, muốn hóa thân vĩnh viễn thành tình yêu muôn thuở. Chọn C.

Giọng điệu chủ đạo của đoạn trích là giọng trách móc nhẹ nhàng. Chọn A.

. Dựa vào từ “đôi ta” → Nhân vật trữ tình trong bài ca dao là lứa đôi chồng vợ. Chọn B.

Thao tác lập luận chính được sử dụng trong đoạn trích trên là chứng minh.

- Tác giả đã đưa ra luận điểm “Bài Thu vịnh của Nguyễn Khuyến mang cái hồn của cảnh vật mùa thu hơn cả” và trích dẫn những lí lẽ, bằng chứng để chứng minh cho ý kiến trên:

+ Tác giả đã trích dẫn những câu thơ tiêu biểu để làm bằng chứng cho ý kiến trên (Song thưa để mặc bóng trăng vào/ Một tiếng trên không ngỗng nước nào / Mấy chùm trước giậu hoa năm ngoái / Nước biếc trông như tầng khói phủ)

+ Tác giả đưa ra những lí lẽ của mình để phân tích các bằng chứng làm nổi bật giá trị của tác phẩm thơ và phục vụ cho luận điểm mà tác giả đưa ra.

=> Các thao tác giải thích, bác bỏ, bình luận không nổi bật trong đoạn trích trên. Chọn B.

Luận cương chính trị (10-1930) của Đảng Cộng sản Đông Dương xác định giai cấp lãnh đạo cách mạng là giai cấp công nhân-đội tiên phong là Đảng Cộng sản. Chọn B.

Cuối tháng 9-1953, Bộ Chính trị Trung ương Đảng đã họp bàn kế hoạch quân sự trong Đông-Xuân 1953-1954.

- Nhiệm vụ: tiêu diệt địch là chính.

- Phương hướng chiến lược: Tập trung lực lượng mở những cuộc tiến công vào những hướng quan trọng về chiến lược mà địch tương đối yếu, nhằm tiêu diệt sinh lực địch, giải phóng đất đai, buộc chúng phải phân tán lực lượng, tạo điều kiện thuận lợi để ta tiêu diệt địch.

Chọn D.

Một trong những mục tiêu quan trọng của Hiệp hội các quốc gia Đông Nam Á được nêu trong Hiệp ước Bali là tăng cường hợp tác phát triển có hiệu quả trong các lĩnh vực kinh tế, văn hóa, xã hội. Chọn B.

Sau Chiến tranh thế giới thứ nhất, kinh tế Việt Nam có những chuyển biến to lớn là do thực dân Pháp thi hành chính sách khai thác thuộc địa lần thứ hai (1919-1929).

Cách mạng tháng Mười (1917) ở Nga đã mở ra con đường giải phóng dân tộc và giải phóng giai cấp cho nhiều quốc gia trên thế giới trong đó có Việt Nam. Nguyễn Ái Quốc đã tiếp nhận và truyền bá vào nước ta hình thành khuynh hướng cách mạng vô sản ở Việt Nam. Chọn C.

Ngày 3-5-1947, ban hành Hiến pháp mới quy định Nhật là nước quân chủ lập hiến (nhưng thực tế là chế độ dân chủ đại nghị tư sản). Theo đó Nhật cam kết từ bỏ việc tiến hành chiến tranh, không dùng hoặc đe dọa sử dụng vũ lực trong quan hệ quốc tế; không duy trì quân đội thường trực, chỉ có lực lượng Phòng vệ dân sự bảo đảm an ninh, trật tự trong nước.Không mang quân đội ra nước ngoài. Chọn D.

Lãnh thổ Liên Bang Nga rộng nhất thế giới.

- A. rộng nhất thế giới. → đúng. Chọn A.

- B. nằm hoàn toàn ở châu Âu. → sai, cả châu Âu và châu Á.

- C. giáp Ân Độ Dương. → Liên Bang Nga không giáp Ản Độ Dương.

- D. liền kề với Đại Tây Dương. → Liên bang Nga không liền kề Đại Tây Dương.

Mất an ninh lương thực liên quan trực tiếp đến làm suy giảm chất lượng cuộc sống. Chọn C.

Kinh tế Nhà nước giữ vai trò chủ đạo vì đang nắm giữ các ngành và lĩnh vực kinh tế then chốt.

A. Chiếm tỉ trọng cao nhất trong cơ cấu GDP. → Kinh tế Nhà nước không chiếm tỉ trọng cao nhất trong GDP.

B. Nắm giữ các ngành và lĩnh vực kinh tế then chốt. → đúng. Chọn B.

C. Chi phối tất cả các thành phần kinh tế khác. → sai, không chi phối tất cả các ngành.

D. Số lượng doanh nghiệp thành lập mới nhiều nhất. → sai, không có nhiều số lượng doanh nghiệp thành lập mới nhiều nhất.

Đông Nam Bộ không có giá trị sản xuất nông nghiệp lớn nhất. Các phương án còn lại là chính xác. Chọn D.

Hằng số điện môi là một đặc trưng quan trọng cho tính chất điện của một chất cách điện. Do vậy không có ý nghĩa gì khi nói về hằng số điện môi của dung dịch muối. Chọn D.

Hiện tượng phản xạ toàn là hiện tượng phản xạ toàn bộ tia sáng tới, xảy ra ở mặt phân cách giữa hai môi trường trong suốt. Điều kiện xảy ra phản xạ toàn phần là n₁ > n₂, i ≥ i_gh.

Chọn D.

Theo định luật khúc xạ ánh sáng: Tia khúc xạ nằm trong mặt phẳng tới và nằm phía bên kia pháp tuyến so với tia tới.

Tia IR₁ là tia khúc xạ, tia IR₂ là tia phản xạ, tia IR₃ là tia tới. Chọn A.

Chế độ rọi sáng vào quang trở không đổi nên điện trở của quang trở là một hằng số.

Mối quan hệ giữa U và I khi R không đổi nên đồ thị I = f(U) là một đường thẳng đi qua gốc tọa độ. Chọn D.

Trong các môi trường đề bài cho, tốc độ truyền âm có giá trị lớn nhất khi truyền trong kim loại và nhỏ nhất khi truyền trong không khí. Chọn B.

Những vị trí vân sáng là những vị trí trùng nhau.

Ta có \(\frac{{{k_1}}}{{{k_2}}} = \frac{{{{\rm{\lambda }}_{\rm{2}}}}}{{{{\rm{\lambda }}_{\rm{1}}}}} = \frac{5}{3}\), khoảng vân trùng \({i_t} = {k_1}{i_1} = {k_1}\frac{{{{\rm{\lambda }}_{\rm{1}}}D}}{a} = 4,5\;\)mm.

Vị trí cảm biến quang hiện số "0" lần đầu tiên chính là vân tối trùng đầu tiên nên ta có \({{\rm{x}}_{{\rm{tt}}}} = ({\rm{k}} + 0,5){{\rm{i}}_{\rm{t}}} = (0 + 0,5).4,5 = 2,25\;\)mm. Chọn D.

Ta có \(_{92}^{235}{\rm{U}} + _0^1{\rm{n}} \to _{39}^{95}{\rm{Y}} + _{53}^{138}{\rm{I}} + 3_0^1{\rm{n}}\), do vậy X là \(_{53}^{138}{\rm{I}}\). Chọn A.

+ Độ dãn của lò xo tại vị trí cân bằng \(\Delta \ell  = \frac{{{\rm{mg}}}}{{\rm{k}}} = \frac{{{{\rm{T}}^2}\;{\rm{g}}}}{{4{{\rm{\pi }}^2}}} = \frac{{0,{5^2}.10}}{{4.10}} = 0,0625\;{\rm{m}} = 6,25\;{\rm{cm}}{\rm{.}}\)

+ Biên độ \({\rm{A}} = 12,5\;{\rm{cm}}{\rm{.}}\)

Thấy \(\Delta \ell  < {\rm{A}} \Rightarrow \) Lực đàn hồi có độ lớn cực tiểu tại vị trí lò xo không biến dạng \({\rm{x}} =  - \Delta \ell  =  - \frac{{\rm{A}}}{2}\).

Thời gian ngắn nhất kể từ \(t = 0\) đến khi lực đàn hời của lò xo có độ lớn cực tiểu: \(\Delta t = \frac{{\Delta {\rm{\varphi }}}}{{\rm{\omega }}}\).

Từ vòng tròn lượng giác, ta có \(\Delta {\rm{\varphi }} = \frac{{7{\rm{\pi }}}}{6} \Rightarrow \Delta t = \frac{{\frac{{7{\rm{\pi }}}}{6}}}{{\frac{{2{\rm{\pi }}}}{{0,5}}}} = \frac{7}{{24}}s\). Chọn C.

Quy bài toán từ \({\rm{f}} \to \infty \)

+ TH1: Xét \({U_C} = U \Leftrightarrow {Z_{C1}} = Z \Rightarrow {R^2} = 2{Z_{{\rm{L}}1}}{Z_{C1}} - Z_{L1}^2\)

+ TH2: Xét \({{\rm{U}}_{\rm{L}}} = {\rm{U}} \Rightarrow {{\rm{Z}}_{{\rm{L}}2}} = {\rm{Z}} \Rightarrow {{\rm{R}}^2} = 2{{\rm{Z}}_{{\rm{L}}2}}{{\rm{Z}}_{{\rm{C}}2}} - {\rm{Z}}_{{\rm{C}}2}^2 = 2{{\rm{Z}}_{{\rm{L}}1}}{{\rm{Z}}_{{\rm{C}}1}} - {\rm{Z}}_{{\rm{L}}1}^2\)

\(\frac{{2\;{\rm{L}}}}{{\rm{C}}} - \frac{1}{{{{({\rm{C\omega }})}^2}}} = \frac{{2\;{\rm{L}}}}{{\rm{C}}} - {({\rm{L\omega }})^2} \Rightarrow 1 = {\left( {{\rm{LC\omega }}{{\rm{\omega }}_0}} \right)^2} \Rightarrow {\rm{LC\omega }}{{\rm{\omega }}_0} = 1\)

Đồng thời \(\cos {{\rm{\varphi }}_2} = \frac{1}{{\sqrt 3 }} \Rightarrow \sin {{\rm{\varphi }}_2} = \frac{{\sqrt 6 }}{3} = \frac{{{U_{\rm{L}}} - {U_C}}}{U} = \frac{{{U_L} - {U_C}}}{{{U_L}}} = 1 - \frac{{{U_C}}}{{{U_L}}} \Rightarrow \frac{{{Z_C}}}{{{Z_L}}} = 1 - \frac{{\sqrt 6 }}{3}\)

\(\frac{1}{{{\mathop{\rm LC}\nolimits} {\omega ^2}}} = 1 - \frac{{\sqrt 6 }}{3}\left( {{\rm{\omega }} = {{\rm{\omega }}_0} + 150{\rm{\pi }}} \right) \Rightarrow {\mathop{\rm LC}\nolimits} = \frac{{3 + \sqrt 6 }}{{{{\rm{\omega }}^2}}}(2)\)

Ta có: \(1 = \left[ {(3 + \sqrt 6 )\frac{{{{\rm{\omega }}_0}}}{{\rm{\omega }}}} \right] \Rightarrow {\rm{\omega }} = (3 + \sqrt 6 ){{\rm{\omega }}_0} \Rightarrow {\rm{f}} = (3 + \sqrt 6 ){{\rm{f}}_0} \Rightarrow {\rm{f}} \approx 16,9\;{\rm{Hz}}\). Đáp án. 16,9.

Ta có \({{\rm{\lambda }}_1} = \frac{{hc}}{{{E_3} - {E_1}}};{{\rm{\lambda }}_2} = \frac{{hc}}{{{E_5} - {E_2}}} \Rightarrow \frac{{{{\rm{\lambda }}_{\rm{1}}}}}{{{{\rm{\lambda }}_{\rm{2}}}}} = \frac{{{E_5} - {E_2}}}{{{E_3} - {E_1}}} \Rightarrow \frac{{{{\rm{\lambda }}_{\rm{1}}}}}{{{{\rm{\lambda }}_{\rm{2}}}}} = \frac{{\frac{{ - 13,6}}{{{5^2}}} - \frac{{ - 13,6}}{{{2^2}}}}}{{\frac{{ - 13,6}}{{{3^2}}} - \frac{{ - 13,6}}{{{1^2}}}}} = \frac{{189}}{{800}}\).

Chọn C.

Đồ thị cho thấy khi tăng nhiệt độ, nồng độ chất tan \(\left( {{\rm{g}}/100\;{\rm{g}}{{\rm{H}}_2}{\rm{O}}} \right)\) giảm dần. Vậy dựa trên số liệu bảng thấy thể hiện rõ nhất mối quan hệ giữa độ tan và nhiệt độ của HCl. Chọn A.

Lưu ý: Trong môi trường kiềm thì fructose và glucose có thể chuyển hoá qua lại lẫn nhau.

Fructose Glucose

\({{\rm{n}}_ \downarrow } = \frac{{0,432}}{{108}} = 0,004(\;{\rm{mol}})\)

Thí nghiệm 2: Tiến hành để đưa toàn bộ về \({{\rm{C}}_6}{{\rm{H}}_{12}}{{\rm{O}}_6}\) (bao gồm cả saccharose chưa bị thủy phân), xác định được số mol saccharose ban đầu.

\({{\rm{n}}_ \downarrow } = \frac{{2,5488}}{{108}} = 0,0236\,\,(\;{\rm{mol}})\)

Ta có:

Số mol saccharose còn lại trong dung dịch \({\rm{X}} = 0,0059 - 0,001 = 0,0049(\;{\rm{mol}})\)

Nồng độ của saccharose trong dung dịch \({\rm{X}} = \frac{{0,0049}}{{{{5.10}^{ - 3}}}} = 0,98{\rm{M}}{\rm{.}}\)

Chọn B.

Công thức cấu tạo của 2 amino acid: Proline (Pro) và Glycine (Gly) cho thấy mỗi phân tử amino acid chỉ chứa 1 nhóm - \({\rm{COOH}}\) (nhóm chức tham gia phản ứng với \({\rm{NaOH}}\)).

Ta có:

\(\begin{array}{l} - {\rm{COOH}} + {\rm{NaOH}} \to - {\rm{COONa}} + {{\rm{H}}_2}{\rm{O}}\\\quad 0,25\quad \,\,\,\,\,0,25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

\( \Rightarrow V = \frac{{0,25}}{{0,5}} = 0,5\)lít. Chọn A.

A. Đúng. \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) đặc là chất xúc tác, ngoài ra \({{\rm{H}}_2}{\rm{S}}{{\rm{O}}_4}\) đặc hút nước, làm cân bằng chuyển dịch theo chiều thuận Þ tăng hiệu suất phản ứng.

B. Đúng. \({\rm{NaCl}}\) thêm vào làm tăng khối lượng riêng dung dịch, cũng như ester có tan 1 ít cũng bị đẩy ra, làm cho dung dịch phân thành 2 lớp, ester nhẹ hơn nên ở phía trên.

C. Đúng. Phản ứng este hóa là phản ứng thuận nghịch nên ống nghiệm vẫn còn chứa isoamyl alcohol và acetic acid.

D. Sai. Dung dịch \({\rm{NaCl}}\) bão hòa được thêm vào để ester tách ra nhanh hơn.

Chọn D.

Tơ visco là polymer bán tổng hợp.

Tinh bột, cellulose là polymer thiên nhiên.

Chọn B.

Ta có: \({n_{BaS{O_3}}} = \frac{{43,4}}{{217}} = 0,2\,mol\)

Bảo toàn nguyên tố S ta có: \({n_{Fe{S_2}}} = \frac{1}{2}{n_{BaS{O_3}}} = 0,1\,mol\) \( \Rightarrow {{\rm{m}}_{Fe{S_2}}} = 0,1 \cdot 120 = 12\;{\rm{g}}{\rm{.}}\)

Chọn B.

Barium carbonate \(\left( {{\rm{BaC}}{{\rm{O}}_3}} \right)\) không tan trong nước, tan trong môi trường acid:

\[BaC{O_3} + 2{H^ + } \to B{a^{2 + }} + C{O_2} + {H_2}O\]

Loại B. Barium chloride \(\left( {{\rm{BaC}}{{\rm{l}}_2}} \right)\) do tan trong nước.

Loại C. Barium hydroxide \(\left( {{\rm{Ba}}{{({\rm{OH}})}_2}} \right)\) do tan trong nước.

Loại D. Barium sulfate \(\left( {{\rm{BaS}}{{\rm{O}}_4}} \right)\) do không tan trong môi trường acid.

Chọn A.

Các biện pháp làm cân bằng chuyển dịch theo chiều thuận:

+ Giảm nhiệt độ.

+ Tăng áp suất.

+ Tăng nồng độ \({{\rm{N}}_2}\) hoặc \({{\rm{H}}_2}\).

+ Giảm nồng độ NH₃.

Chọn C.

Dung dịch \({\rm{X}}\) làm phenolphthalein hóa hồng nên dung dịch \({\rm{X}}\) có chứa \({\rm{O}}{{\rm{H}}^ - }\)

Þ Cathode điện phân hết \[C{u^{2 + }}\], rồi điện phân nước đến khi anode vừa điện phân hết \(C{l^ - }\)thì dừng điện phân.

\({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3} + 2{\rm{O}}{{\rm{H}}^ - } \to 2{\rm{AlO}}_2^ - + {{\rm{H}}_2}{\rm{O}}\)

Ta có: \({n_{{\rm{C}}{{\rm{l}}_2}}} = \frac{{9,916}}{{24,79}} = 0,4\;{\rm{mol;}}\,{{\rm{n}}_{A{l_2}{O_3}}} = \frac{{20,4}}{{102}} = 0,2\,mol.\)

Þ \({n_{NaCl}} = 2{n_{C{l_2}}} = 0,8\,mol\)

\(\begin{array}{l}{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3} + 2{\rm{O}}{{\rm{H}}^ - } \to 2{\rm{AlO}}_2^ - + {{\rm{H}}_2}{\rm{O}}\\\,\,\,{\rm{0,2}} \to \,\,\,0,4\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,({\rm{mol)}}\end{array}\)

Xét quá trình điện phân ở 2 cực:

Bảo toàn electron: \(2{{\rm{n}}_{{\rm{C}}{{\rm{u}}^{2 + }}}} + {{\rm{n}}_{{\rm{O}}{{\rm{H}}^ - }}} = 2{{\rm{n}}_{{\rm{C}}{{\rm{l}}_2}}} \Rightarrow {{\rm{n}}_{{\rm{C}}{{\rm{u}}^{2 + }}}} = 0,2\) mol.

\( \Rightarrow {\rm{m}} = 0,2 \cdot 160 + 0,8 \cdot 58,5 = 78,8\,(\;{\rm{g}})\).

Đáp án: 78,8

Các đặc điểm đúng là I, II, III.

IV. Sai. Ngoài hoocmôn thực vật gây kích thích sinh trưởng còn có hoocmôn gây ức chế sinh trưởng.

Chọn A.

- Nguyên nhân của hiện tượng cụp lá của cây trinh nữ khi va chạm là do sức trương của nửa dưới của các chỗ phình bị giảm do nước di chuyển vào những mô lân cận.

- Nguyên nhân của hiện tượng đóng mở khí khổng là do sự biến động hàm lượng nước trong tế bào khí khổng.

Chọn B.

- Một trong những nguyên nhân có thể giải thích cho việc nhịp tim của trẻ em thường cao hơn người trưởng thành là do cơ thể của trẻ em đang trong giai đoạn phát triển, cần nhiều dưỡng khí và chất dinh dưỡng.

- Các ý còn lại sai do:

+ Cấu tạo của tim trẻ không phức tạp hơn người trưởng thành.

+ Hoạt động lao động nặng nhọc của người lớn thường tiêu tốn nhiều năng lượng hơn so với hoạt động vui chơi của trẻ.

+ Người lớn thường gặp phải áp lực công việc ảnh hưởng đến tâm lí nhiều hơn trẻ nhỏ.

Chọn B.

Trong quá trình nhân đôi ADN, nuclêôtit guanin của môi trường nội bào liên kết bổ sung với nuclêôtit xitôzin và ngược lại, nuclêôtit timin của môi trường nội bào liên kết bổ sung với nuclêôtit ađênin và ngược lại. Chọn B.

Có 6 nhóm gen liên kết → 2n = 12. Vậy thể một chứa 2n - 1 = 11, thể ba chứa 2n + 1 = 13, thể tam bội chứa 3n = 18. Ở kì sau của nguyên phân, các NST đã nhân đôi và tách ra phân li về 2 phía nên số lượng NST trong thể một, thể ba, thể tam bội lần lượt là: 22, 26, 36. Chọn B.

Cây cho hạt phấn có kiểu gen: AaBbDdee.

A. Sai. Cây cho hạt phấn mang cặp ee nên không thể tạo ra cây có kiểu gen mang cặp EE.

B. Đúng. Các cây tạo ra bằng phương pháp nuôi cấy hạt phấn sau đó lưỡng bội hóa có kiểu gen thuần chủng nên khi giảm phân chỉ cho 1 loại giao tử.

C. Sai. Các cây này có thể có kiểu gen khác nhau nên kiểu hình khác nhau.

D. Sai. Số kiểu gen tối đa = số loại giao tử được tạo ra = 2³ = 8.

Chọn B.

A. Sai. Hội chứng suy giảm miễn dịch do HIV gây ra có ở cả nam và nữ.

B. Đúng. Hội chứng Tơcnơ mang XO – thiếu 1 NST X, chỉ xuất hiện ở nữ.

C. Sai. Hội chứng Claiphentơ mang XXY – thừa 1 NST X, chỉ xuất hiện ở nam.

D. Sai. Hội chứng Đao mang 3 NST số 21, có ở cả nam và nữ.

Chọn B.

Có 2 phát biểu đúng là I và III.

I. Đúng. Vì chuỗi thức ăn này có 5 mắt xích, trong đó chỉ có cỏ là sinh vật sản xuất; còn các loài còn lại đều là sinh vật tiêu thụ.

II. Sai. Vì hiệu suất sinh thái của mỗi bậc dinh dưỡng thường chỉ đạt khoảng 10%. Do đó, tổng sinh khối của các loài tiêu thụ chỉ chiếm khoảng 11,11% so với tổng sinh khối của cỏ.

III. Đúng. Vì chất độc sẽ được tích lũy qua chuỗi thức ăn, ở bậc dinh dưỡng càng cao thì lượng độc tố được tích lũy trong cơ thể càng lớn.

IV. Sai. Vì khi sâu bị giảm số lượng thì các loài nhái, rắn, diều hâu đều giảm số lượng.

Chọn C.

Muốn xác định nhân tố gây nên sự thay đổi cấu trúc di truyền thì phải dựa vào sự thay đổi tần số alen qua mỗi thế hệ.

- \({F_1}\) có tần số alen A = 0,64 + 0,32/2 = 0,8.

- \({F_2}\) có tần số alen A = 0,64 + 0,32/2 = 0,8.

- \({F_3}\) có tần số alen A = 0,2 + 0,4/2 = 0,4.

- \({F_4}\) có tần số alen A = 0,16 + 0,48/2 = 0,4.

- \({F_5}\) có tần số alen A = 0,16 + 0,48/2 = 0,4.

Như vậy, tần số alen chỉ thay đổi ở giai đoạn từ F₂ sang F₃ và sự thay đổi này diễn ra một cách đột ngột (tần số A từ 0,8 chuyển xuống còn 0,4) nên quần thể trên đã chịu tác động của các yếu tố ngẫu nhiên. Chọn A.

Các cây đồng hợp tử mang 2 tính trạng trội ở \({{\rm{F}}_3}\) gồm: \(\frac{{{\rm{Ab}}}}{{{\rm{Ab}}}}\frac{{{\rm{dE}}}}{{{\rm{dE}}}};\frac{{{\rm{Ab}}}}{{{\rm{Ab}}}}\frac{{{\rm{De}}}}{{{\rm{De}}}};\frac{{{\rm{aB}}}}{{{\rm{aB}}}}\frac{{{\rm{De}}}}{{{\rm{De}}}}\) chiếm tỉ lệ:

\(\begin{array}{l} = 0,3 \times \left( {\frac{{1 - \frac{1}{{{2^3}}}}}{2}\frac{{Ab}}{{Ab}}} \right) \times 1\frac{{dE}}{{dE}} + 0,6 \times \left( {\frac{{1 - \frac{1}{{{2^3}}}}}{2}\frac{{{\rm{Ab}}}}{{{\rm{Ab}}}}} \right)\left( {\frac{{1 - \frac{1}{{{2^3}}}}}{2}\frac{{{\rm{De}}}}{{{\rm{De}}}}} \right) + 0,6 \times \left( {\frac{{1 - \frac{1}{{{2^3}}}}}{2}\frac{{{\rm{aB}}}}{{{\rm{aB}}}}} \right)\left( {\frac{{1 - \frac{1}{{{2^3}}}}}{2}\frac{{{\rm{De}}}}{{{\rm{De}}}}} \right)\\ = \frac{{231}}{{640}}\end{array}\)

Đáp án: \(\frac{{231}}{{640}}.\)

Đoạn trích trên nói về hiện tượng nổi bật của các biến động dân số ở Thăng Long - Hà Nội. Chọn A.

Theo đoạn trích các luồng di cư thuộc tầng lớp tinh hoa, nông thôn và lao động qua quá trình di cư đều cư trú tại Thăng Long. Người di cư ra khỏi thành phố thì không còn cư trú tại Thăng Long, làm cho số lượng cư dân khu vực đô thị giảm đi nhanh chóng. Chọn A.

Cây xà nu “phóng lên” có nghĩa là cây sinh sôi, phát triển, vươn lên. Chọn B.