Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 6)

🔥 Học sinh cũng đã học

170 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 1

714 lượt thi 22 câu hỏi

65 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 9

609 lượt thi 22 câu hỏi

44 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 8

588 lượt thi 22 câu hỏi

33 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 7

577 lượt thi 22 câu hỏi

41 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 6

585 lượt thi 22 câu hỏi

36 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 5

580 lượt thi 22 câu hỏi

41 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 4

585 lượt thi 22 câu hỏi

49 người thi tuần này

Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 3

593 lượt thi 22 câu hỏi

Danh sách câu hỏi:

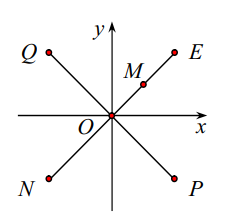
Câu 1

Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z. Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z?

A. Điểm Q

B. Điểm P

C. Điểm E

D. Điểm N

Lời giải

Đáp án đúng là: C

Điểm M(a; b) biểu diễn số phức z = a + bi (a, b $\in$ ℝ)

$\Leftrightarrow$ 2z = 2a + 2bi.

Do đó điểm biểu diễn số phức 2z là E(2a; 2b).

Câu 2

Tìm x + y thỏa mãn (2x – 3yi) + (1 – 3i) = –1 + 6i với i là đơn vị ảo.

A. –4

B. 4

C. 5

D. –2

Lời giải

Đáp án đúng là: A

(2x – 3yi) + (1 - 3i) = -1 + 6i

$\Leftrightarrow$ (2x + 1) – (3y + 3)i = –1 + 6i

$\Rightarrow \{\begin{cases} 2 x + 1 = - 1 \\ 3 y + 3 = - 6 \end{cases}$ $\Leftrightarrow \{\begin{cases} 2 x = - 2 \\ 3 y = - 9 \end{cases}$ $\Leftrightarrow \{\begin{cases} x = - 1 \\ y = - 3 \end{cases}$

Do đó, x + y = (–1) + (–3) = –4.

Câu 3

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M(1; 3; –2), cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho $\frac{O A}{1} = \frac{O B}{2} = \frac{O C}{4}$ .

A. x + 2y + 4z + 1 = 0

B. 2x – y – z – 1 = 0

C. 4x + 2y + z – 8 = 0

D. x + 2y + 4z + 10 = 0

Lời giải

Đáp án đúng là: C

Ta có: $\frac{O A}{1} = \frac{O B}{2} = \frac{O C}{4} = m$

$\Rightarrow$ OA = m; OB = 2m; OC = 4m

Do mặt phẳng (P) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C nên tọa độ các điểm A, B, C lần lượt là A(m; 0; 0), B(0; 2m; 0), C(0; 0; 4m).

Mặt phẳng đoạn chắn (P) có phương trình là: $\frac{x}{m} + \frac{y}{2 m} + \frac{z}{4 m} = 1$

Do M $\in$ (P) nên ta có: $\frac{1}{m} + \frac{3}{2 m} - \frac{2}{4 m} = 1$

$\Leftrightarrow \frac{1}{2 m} + \frac{3}{2 m} - \frac{1}{m} = 1$

$\Leftrightarrow \frac{4}{2 m} = 1 \Leftrightarrow m = 2$

Từ đó, (P): $\frac{x}{2} + \frac{y}{4} + \frac{z}{8} = 1$

$\Leftrightarrow$ 4x + 2y + z – 8 = 0.

Câu 4

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 1; 1) và B(1; 2; 3). Viết phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB.

A. x + 3y + 4z – 26 = 0

B. x + y + 2z – 6 = 0

C. x + 3y + 4z – 7 = 0

D. x + y + 2z – 3 = 0

Lời giải

Đáp án đúng là: D

Ta có: $\vec{A B} = (1; 1; 2)$

Vì $\vec{A B} ⊥ (P)$ nên vectơ pháp tuyến của (P) là $\vec{n} = (1; 1; 2)$

Mặt phẳng (P) có vectơ pháp tuyến là và đi qua điểm A(0; 1; 1) có phương trình:

x + (y – 1) + 2(z – 1) = 0

$\Leftrightarrow$ x + y – 1 + 2z – 2 = 0

$\Leftrightarrow$ x + y + 2z – 3 = 0.

Câu 5

Trong không gian Oxyz, hình chiếu vuông góc của điểm A(1; 2; 5) trên trục Ox có tọa độ là

A. (1; 0; 0)

B. (0; 2; 5)

C. (0; 0; 5)

D. (0; 2; 0)

Lời giải

Đáp án đúng là: A

Theo lý thuyết ta có:

Hình chiếu của điểm A(x; y; z) lên trục Ox có tọa độ là A₁(x; 0; 0)

Vậy nên, hình chiếu của điểm A(1; 2; 5) lên trục Ox có tọa độ là A₁(1; 0; 0).

Câu 6

Cho hàm số y = f (x) liên tục trên ℝ. Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f (x), y = 0, x = –1 và x = 5 (như hình vẽ bên).

Mệnh đề nào sau đây đúng?

A. $- \int_{- 1}^{1} f (x) d x - \int_{1}^{5} f (x) d x$ .

B. $\int_{- 1}^{1} f (x) d x + \int_{1}^{5} f (x) d x$ .

C. $\int_{- 1}^{1} f (x) d x - \int_{1}^{5} f (x) d x$ .

D. $- \int_{- 1}^{1} f (x) d x + \int_{1}^{5} f (x) d x$ .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học