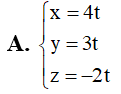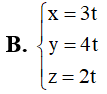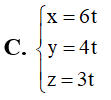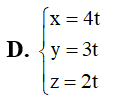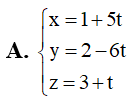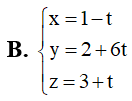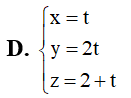Bài tập Hình học không gian OXYZ cơ bản, nâng cao có lời giải (P8)
28 người thi tuần này 4.6 18 K lượt thi 30 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 3
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 2
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 1
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 3
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án C.
Do H là trực tâm tam giác ABC suy ra được H là hình chiếu vuông góc của O trên mặt phẳng (ABC) (học sinh tự chứng minh).
![]()
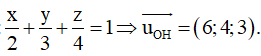
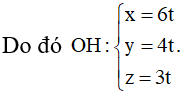
Lời giải
Đáp án D
Phương pháp: Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
Cách giải:
Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
![]()
![]()
![]()
Câu 3
A. -2 - x
B. 3x + 2
C. 3x - 2
D. x + 2
Lời giải
Đáp án C
Phương pháp:
![]()
![]()
Cách giải:
![]()
Lời giải
Đáp án A
Phương pháp:
Mặt cầu có đường kính AB nhận trung điểm của AB làm tâm và có bán kính R =
Cách giải: Gọi I là trung điểm của AB ta có I(1;1;1)
![]()
Vậy mặt cầu đường kính AB có tâm I(1;1;1) và bán kính R ==
![]()
Lời giải
Đáp án D
Phương pháp :
Gọi (Q): x+y+z+a=0 là mặt phẳng song song với mặt phẳng (P).
Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải :
Gọi (Q): x+y+z+a=0 là mặt phẳng song song với mặt phẳng (P).
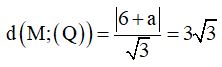

![]()
![]()
Vậy không có mặt phẳng (Q) nào thỏa mãn điều kiện bài toán.
Câu 6
A. (-2;1;1)
B. (-4;2;3)
C. (4;2;-2)
D. (4;-2;2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. x+4y-2z=0
B.
C.
D. x+4y-2z-8=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Cho mặt phẳng đi qua M(1;-3;4) và song song với mặt phẳng : 6x -5y+z-7=0. Phương trình mặt phẳng là:
A. 6x-5y+z+25=0
B. 6x-5y+z-25=0
C. 6x-5y+z-7=0
D. 6x-5y+z+17=0
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Cho mặt phẳng đi qua M(1;-3;4) và song song với mặt phẳng : 6x +2y-z-7=0. Phương trình mặt phẳng là:
A. 6x +2y-z+8=0.
B. 6x +2y-z+4=0.
C. 6x +2y-z-4=0.
D. 6x +2y-z-17=0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. H(3;0;2)
B. H(-1;4;4)
C. H(2;0;3)
D. H(4;4;-1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. (1;0;3)
B. (-1;1;-1)
C. (2;-2;3)
D. (1;1;-1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. M(2;0;5)
B. M(1;2;3)
C. M(3;-2;7)
D. M(3;0;4)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. N(-2;0;1)
B.
C.
D. N(-1;2;1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. (-6;-2;10)
B. (-1;2;4)
C. (6;2;-10)
D. (1;-2;-4)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. 2a-b=3
B. 2a-b=2
C. 2a-b=-2
D. 2a-b=4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. H(1;2;2)
B. H(2;5;3)
C. H(6;7;8)
D. H(2;-3;-1)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. -10
B. 10
C. 12
D. -20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. =(1;-1;3)
B. =(2;-1;3)
C. =(2;1;3)
D. =(2;3;-2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.