Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 27)

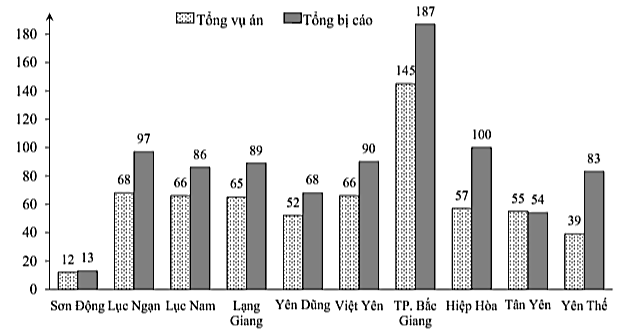
Số bị cáo của Thành phố Bắc Giang là 187.

Số bị cáo của huyện Lục Ngạn là 97.

Số bị cáo của TP. Bắc Giang nhiều hơn số bị cáo của huyện Lục Ngạn là \(\frac{{187 - 97}}{{97}} \cdot 100\% \approx 92,78\% .\) Chọn D.

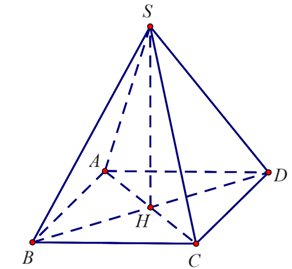
Gọi khối chóp tứ giác đều là \[S.ABCD\] có đáy là hình vuông cạnh \(230\;\,{\rm{m}}\), chiều cao \(SH = 147\;\,{\rm{m}}.\)

Thể tích của kim tự tháp là:

\({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SH = \frac{1}{3} \cdot \left( {{{230}^2}} \right) \cdot 147 = 2\,\,592\,\,100\,\,\left( {{{\rm{m}}^3}} \right).\)

Số tiền anh A cần tiết kiệm là \(500 - 500 \cdot 0,32 = 340\) (triệu đồng).

Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là \({u_1} = 10\) (triệu đồng).

Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là:

\({u_2} = {u_1} \cdot \left( {1 + 0,12} \right) = {u_1} \cdot 1,12\) (triệu đồng).

Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ ba là:

\({u_3} = {u_1} \cdot {\left( {1 + 0,12} \right)^2} = {u_1} \cdot {\left( {1,12} \right)^2}\) (triệu đồng).

Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ \(n\) là

\({u_n} = {u_1} \cdot {\left( {1 + 0,12} \right)^{n - 1}} = {u_1} \cdot {\left( {1,12} \right)^{n - 1}}\)

Vậy số tiền mà anh A tiết kiệm được sau \(n\) năm là

12. \(\left( {{u_2} - {u_1} + {u_3} - {u_2} + \ldots + {u_{n - 1}} - {u_{n - 2}} + {u_n} - {u_{n - 1}}} \right) = 12\left( {{u_n} - {u_1}} \right)\)

\( = 12 \cdot \left[ {{u_1} \cdot {{\left( {1,12} \right)}^{n - 1}} - {u_1}} \right] = 340\) với \({u_1} = 10\) suy ra \(n \approx 13\) năm. Chọn C.

Ta có: \(\overrightarrow {AB} = \left( {0\,;\,\,2\,;\,\, - 1} \right)\,,\,\,\overrightarrow {AC} = \left( { - 1\,;\,\,1\,;\,\,2} \right),\,\,\overrightarrow {AD} = \left( { - 3\,;\,\,m + 2\,;\,\,n} \right)\);

\[\left[ {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\1&2\end{array}} \right|\,;\,\,\left| {\begin{array}{*{20}{c}}{ - 1}&0\\2&{ - 1}\end{array}} \right|;\,\,\left| {\begin{array}{*{20}{c}}0&2\\{ - 1}&1\end{array}} \right|} \right) = \left( {5\,;\,\,1\,;\,\,2} \right)\].

Bốn điểm \[A\,,\,\,B\,,\,\,C\,,\,\,D\] đồng phẳng \( \Leftrightarrow \left[ {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right] \cdot \overrightarrow {AD} = 0\)

\( \Leftrightarrow - 15 + m + 2 + 2n = 0 \Leftrightarrow m + 2n = 13.{\rm{ }}\)Chọn C.

Ta có \({z^2} - 6z + 73 = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{z_1} + {z_2} = 6}\\{{z_1}{z_2} = 73}\end{array}} \right.\).

Khi đó \(z_1^2 + z_2^2 - \left| {{z_1}} \right| \cdot \left| {{z_2}} \right| = {\left( {{z_1} + {z_2}} \right)^2} - 2{z_1}{z_2} - \left| {{z_1}{z_2}} \right| = {6^2} - 2 \cdot 73 + 73 = - 37.\)

Chọn C.

Ta có: \(AH = 1,6\,\;{\rm{m }};\,\,HB = 10\,\;{\rm{m }};\,\,\widehat {BAC} = 30^\circ .\)

Trong tam giác \[AHB\] có: \(\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{{1,6}}{{10}} = 0,16 \Rightarrow \widehat {ABH} = 9^\circ 5'\).

Suy ra \(\widehat {ABC} = 90^\circ - \widehat {ABH} = 80^\circ 55'\); \(\widehat {ACB} = 180^\circ - \left( {\widehat {BAC} + \widehat {ABC}} \right) = 69^\circ 5'\).

Áp dụng định lý sin trong tam giác \[ABC\] có:

\(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{CB}}{{\sin \widehat {BAC}}} \Rightarrow CB = \frac{{AB \cdot \sin \widehat {BAC}}}{{\sin \widehat {ACB}}} \approx 5,42\;\,({\rm{m)}}{\rm{. }}\)Chọn D.

Đặt \(u = \ln x \Rightarrow u' = \frac{1}{x} > 0\,,\,\,\forall x \in \left( {1\,;\,\,e} \right)\) và \(u \in \left( {0\,;\,\,1} \right).\)

Khi đó \(y = \frac{{u - 4}}{{u - 2m}} \Rightarrow y' = u' \cdot \frac{{4 - 2m}}{{{{\left( {u - 2m} \right)}^2}}} > 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4 - 2m > 0}\\{u \ne 2m}\end{array}} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l} - 2m > - 4\\2m \notin \left( {0\,;\,\,1} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 2\\\left[ \begin{array}{l}2m \ge 1\\2m \le 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m < 2\\\left[ \begin{array}{l}m \ge \frac{1}{2}\\m \le 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{2} \le m < 2\\m \le 0\end{array} \right.\).

Kết hợp với \(m \in \left[ { - 2019\,;\,\,2019} \right]\) và \(m \in \mathbb{Z}\), suy ra ta có \(2020 + 1 = 2021\) giá trị nguyên \[m.\]

Chọn B.

Đặt \(\left\{ {\begin{array}{*{20}{l}}{u = \ln \left( {{x^2} + 9} \right)}\\{{\rm{d}}v = x\;{\rm{d}}x}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{d}}u = \frac{{2x}}{{{x^2} + 9}}\;{\rm{d}}x}\\{v = \frac{{{x^2} + 9}}{2}}\end{array}} \right.} \right.\) .

Suy ra \(I = \left. {\frac{{{x^2} + 9}}{2} \cdot \ln \left( {{x^2} + 9} \right)} \right|_0^4 - \int\limits_0^4 {\frac{{2x}}{{{x^2} + 9}} \cdot } \frac{{{x^2} + 9}}{2}{\rm{d}}x\)

\( = \left( {\frac{{25}}{2} \cdot \ln 25 - \frac{9}{2} \cdot \ln 9} \right) - \int\limits_0^4 {xdx} = 25 \cdot \ln 5 - 9 \cdot \ln 3 - 8 = a \cdot \ln 5 + b \cdot \ln 3 + c\).

Suy ra \(a = 25\,,\,\,b = - 9\,,\,\,c = - 8\) nên \(T = a + b + c = 8.\) Chọn C.

TH1: Lấy hai điểm thuộc \({d_1}\) và một điểm thuộc \({d_2}\), suy ra có tất cả \(C_{10}^2 \cdot C_n^1\) tam giác.

TH2: Lấy một điểm thuộc \({d_1}\) và hai điểm thuộc \({d_2}\), suy ra có tất cả \(C_{10}^1 \cdot C_n^2\) tam giác.

Khi đó, tổng số tam giác được tạo thành là \(C_{10}^2 \cdot C_n^1 + C_{10}^1 \cdot C_n^2 = 1725.\)

Thử đáp án, ta thấy \(n = 15.\) Chọn B.

Ta có \(\log _2^2\left( {4x} \right) - {\log _{\sqrt 2 }}\left( {2x} \right) - 5 = 0\)\( \Leftrightarrow {\left[ {{{\log }_2}\left( {4x} \right)} \right]^2} - {\log _{2\frac{1}{2}}}\left( {2x} \right) - 5 = 0\)

\( \Leftrightarrow {\left( {{{\log }_2}4 + {{\log }_2}x} \right)^2} - 2{\log _2}\left( {2x} \right) - 5 = 0\)\( \Leftrightarrow {\left( {2 + {{\log }_2}x} \right)^2} - 2\left( {1 + {{\log }_2}x} \right) - 5 = 0\)

\( \Leftrightarrow {\left( {{{\log }_2}x} \right)^2} + 2{\log _2}x - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\log }_2}x = 1}\\{{{\log }_2}x = - 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = \frac{1}{8}}\end{array}} \right.} \right..\)

Vậy nghiệm nhỏ nhất của phương trình là \(x = \frac{1}{8}.\) Chọn A.

Gọi \(P\left( t \right)\) là lợi nhuận phát sinh của vốn sau \(t\) năm đầu tư.

Ta có \(P\left( t \right)\) là nguyên hàm của hàm tốc độ \(P'\left( t \right)\).

Lợi nhuận phát sinh sau 10 năm đầu tiên là \(\int\limits_0^{10} {P'\left( t \right)dt} = \frac{{4780}}{3}\) (triệu đồng). Chọn D.

Vẽ đường thẳng \({d_1}:x - y - 1 = 0\), đường thẳng \({d_1}\) qua hai điểm \((0; - 1)\) và \((1;0).\)

Vẽ đường thẳng \({d_2}:x + 2y - 10 = 0\), đường thẳng \({d_2}\) qua hai điểm \((0;5)\) và \((2;4).\)

Vẽ đường thẳng \({d_3}:y = 4.\)

Miền nghiệm của hệ bất phương trình là miền ngũ giác \[ABCOE\] với \(A\left( {4\,;\,\,3} \right),\,\,B\left( {2\,;\,\,4} \right),\)\(C\left( {0\,;\,\,4} \right),\,\,E\left( {1\,;\,\,0} \right).\)

Ta có: \(F\left( {4\,;\,\,3} \right) = 10\,,\,\,F\left( {2\,;\,\,4} \right) = 10\,,\,\,F\left( {0\,;\,\,4} \right) = 8\,,\,\,F\left( {1\,;\,\,0} \right) = 1\,,\,\,F\left( {0\,;\,\,0} \right) = 0.\)

Vậy giá trị lớn nhất của biểu thức \(F\left( {x\,;\,\,y} \right) = x + 2y\) bằng 10. Chọn C.

Cách 1: Ta có mặt phẳng \((\alpha )\) nhận vectơ \(\overrightarrow {{n_\alpha }} = \left( {1\,;\,\,1\,;\,\,1} \right)\) là vectơ pháp tuyến, đường thẳng \(d\) đi qua điểm \(A\left( {0\,;\,\, - 1\,;\,\,2} \right)\) và nhận \(\overrightarrow {{u_d}} = \left( {1\,;\,\,2\,;\,\, - 1} \right)\) là vectơ chỉ phương.

Gọi \(\left( \beta \right)\) là mặt phẳng chứa đường thẳng \(d\) và vuông góc với mặt phẳng \(\left( \alpha \right).\)

Ta có \(\overrightarrow {{n_\beta }} = \overrightarrow {{n_\alpha }} \wedge \overrightarrow {{n_d}} = \left( { - 3\,;\,\,2\,;\,\,1} \right).\)

Khi đó đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).

Do đó một vectơ chỉ phương của đường thẳng \(\Delta \) là \(\overrightarrow {{u_\Delta }} = \overrightarrow {{u_\alpha }} \wedge \overrightarrow {{u_\beta }} = \left( { - 1\,;\,\, - 4\,;\,\,5} \right).\)

Mà \(\vec u = \left( {1\,;\,\,a\,;\,\,b} \right)\) nên \(a = 4,\,\,b = - 5.\) Vậy \(a + b = - 1.\)

Cách 2: Dễ dàng tính được tọa độ giao điểm của đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\) là \(I = \left( {1\,;\,\,1\,;\,\,1} \right).\)

Trên đường thẳng lấy điểm \(A\left( {0\,;\,\, - 1\,;\,\,2} \right)\) và gọi \(H\) là hình chiếu vuông góc của \(A\) trên mặt phẳng \((\alpha ).\)

Phương trình đường thẳng đi qua \(A\) và \(H\) có dạng: \(\left\{ {\begin{array}{*{20}{l}}{x = 0 + t}\\{y = - 1 + t}\\{z = 2 + t}\end{array}} \right.\)

Tọa độ của \(H\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = 0 + t}\\{y = - 1 + t}\\{z = 2 + t}\\{x + y + z - 3 = 0}\end{array} \Rightarrow t = \frac{2}{3}} \right..\) Do đó \(H\left( {\frac{2}{3}\,;\,\,\frac{{ - 1}}{3}\,;\,\,\frac{8}{3}} \right).\)

Đường thẳng \(\Delta \) đi qua hai điểm \(I\) và \(H\) nhận vectơ \(\overrightarrow {IH} = \left( {\frac{{ - 1}}{3}\,;\,\,\frac{{ - 4}}{3}\,;\,\,\frac{5}{3}} \right)\) là vectơ chỉ phương nên cũng nhận vectơ \(\overrightarrow {{u_\Delta }} = \left( {1\,;\,\,4\,;\,\, - 5} \right)\) là vectơ chỉ phương.

Vậy \(a + b = - 1.\) Chọn C.

Ta có:

 \(x \cdot f'\left( x \right) = f\left( x \right) - x{f^2}\left( x \right) \Leftrightarrow \frac{{f\left( x \right) - x \cdot f'\left( x \right)}}{{{f^2}\left( x \right)}} = x \Leftrightarrow {\left[ {\frac{x}{{f\left( x \right)}}} \right]^\prime } = x \Rightarrow \frac{x}{{f\left( x \right)}} = \frac{{{x^2}}}{2} + C\).

Do \(f\left( 1 \right) = 1 \Rightarrow C = \frac{1}{2} \Rightarrow f\left( x \right) = \frac{{2x}}{{{x^2} + 1}} \Rightarrow f\left( 2 \right) = \frac{4}{5}.\) Chọn D.

Giả sử mỗi giờ người thứ nhất sơn được \(\frac{1}{x}\) bức tường và người thứ hai sơn được \(\frac{1}{y}\) bức tường.

Khi đó ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{\frac{7}{x} + \frac{4}{y} = \frac{5}{9}}\\{\frac{{11}}{x} + \frac{8}{y} = \frac{{17}}{{18}}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 18}\\{y = 24}\end{array}} \right.} \right.\).

Vậy người thứ nhất sau 18 h thì sơn xong bức tường và người thứ hai sau 24 h thì sơn xong bức tường.

Chọn A.

Điều kiện \(\cos x + 1 \ne 0 \Leftrightarrow x \ne \pi + k2\pi .\)

Ta có \[\frac{{\sin 3x}}{{\cos x + 1}} = 0 \Rightarrow \sin 3x = 0 \Leftrightarrow x = \frac{{k\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right).\]

So với điều kiện nghiệm của phương trình là \(x = \frac{{k\pi }}{3}\) với \(k \in \mathbb{Z}\,,\,\,k \ne 3 \cdot \left( {2l + 1} \right).\)

Vì \(2\pi \le x \le 4\pi \Leftrightarrow 2\pi \le \frac{{k\pi }}{3} \le 4\pi \Leftrightarrow 6 \le k \le 12\) nên ta chọn \[k \in \left\{ {6\,;\,\,7\,;\,\,8\,;\,\,9\,;\,\,10\,;\,\,11\,;\,\,12} \right\}.\]

Chọn B.

Theo công thức lãi kép, ta được:

\(90\,\,728\,\,900 \cdot {\left( {1 + 1,05\% } \right)^{16}} \approx 107\,\,232\,\,574\) (người). Chọn C.

Ta có \(\left( Q \right)\) chứa trục \(Ox \Rightarrow {\vec n_{\left( Q \right)}} \bot {\vec u_{Ox}}\left( {1\,;\,\,0\,;\,\,0} \right).\)

Mà \({\vec n_{\left( Q \right)}} \bot \overrightarrow {OA} \) nên suy ra \({\vec n_{\left( Q \right)}} = \left[ {{{\vec u}_{Ox}}\,;\,\,\overrightarrow {OA} } \right] = \left( {0\,;\,\,1\,;\,\,3} \right).\)

Yêu cầu bài toán \[ \Leftrightarrow {\vec n_{\left( Q \right)}} \cdot {\vec n_{\left( P \right)}} = 0 \Leftrightarrow \left( {0\,;\,\,1\,;\,\,3} \right) \cdot \left( {1\,;\,\, - m\,;\,\,1} \right) = 0 \Leftrightarrow m = 3.\] Chọn D.

\(\left\{ {\begin{array}{*{20}{l}}{5\left| {x - 1} \right| - 3\left| {y + 2} \right| = 7}\\{2\sqrt {4{x^2} - 8x + 4} + 5\sqrt {{y^2} + 4y + 4} = 13}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5\left| {x - 1} \right| - 3\left| {y + 2} \right| = 7}\\{2\sqrt {4{{\left( {x - 1} \right)}^2}} + 5\sqrt {{{\left( {y + 2} \right)}^2}} = 13}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5\left| {x - 1} \right| - 3\left| {y + 2} \right| = 7}\\{4\left| {x - 1} \right| + 5\left| {y + 2} \right| = 13}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left| {x - 1} \right| = 2}\\{\left| {y + 2} \right| = 1}\end{array}} \right.} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = - 1}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{l}}{y = - 3}\\{y = - 1}\end{array}} \right.}\end{array}} \right.\).

Vậy \(\min A = - 1 + 2 \cdot \left( { - 3} \right) = - 7.\) Chọn D.

Ta có \(f\left( x \right) < x + m \Leftrightarrow m > f\left( x \right) - x\) với mọi \(x \in \left( {0\,;\,\,2} \right) \Leftrightarrow m > {\max _{\left( {0\,;\,\,2} \right)}}\left[ {f\left( x \right) - x} \right]\).

Xét hàm số \(g\left( x \right) = f\left( x \right) - x\), có \(g'\left( x \right) = f'\left( x \right) - 1 < 0\,,\,\,\forall x \in \left( {0\,;\,\,2} \right)\).

Suy ra hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( {0\,;\,\,2} \right)\).

Do đó \({\max _{\left( {0\,;\,\,2} \right)}}g\left( x \right) = {\max _{\left( {0\,;\,\,2} \right)}}\left[ {f\left( x \right) - x} \right] = f\left( 0 \right).\)

Vậy \(m \ge f\left( 0 \right).\) Chọn B.

Gọi chiều rộng của bể là \(3x\,\,(\;{\rm{m}}).\)

Ta có chiều dài bể là \(4x\,\,(\;{\rm{m}})\) và chiều cao của bể là \(\frac{2}{{3{x^2}}}\,\,({\rm{m}}).\)

Khi đó tổng diện tích bề mặt xây là

\(T = \left( {3x + 4x} \right) \cdot 2 \cdot \frac{2}{{3{x^2}}} + 2 \cdot 3x \cdot 4x - \frac{2}{9} \cdot 3x \cdot 4x\)\( = \frac{{28}}{{3{x^2}}} + \frac{{64{x^2}}}{3} \ge 2 \cdot \sqrt {\frac{{28}}{{3{x^2}}} \cdot \frac{{64{x^2}}}{3}} = \frac{{32\sqrt 7 }}{3}\,\,\left( {\;{{\rm{m}}^2}} \right)\).

Chi phí thấp nhất mà ông Nam phải chi trả để xây dựng bể nước là:

\(T \cdot 980\,\,000 \ge \frac{{32\sqrt 7 }}{3} \cdot 980\,\,000 \approx 27\,\,657\,\,000\) (đồng). Chọn B.

Ta có: \(f\left( x \right) = {x^2} - 2x - \frac{{10}}{9}\int\limits_0^1 {f\left( x \right) \cdot f'\left( x \right){\rm{d}}x} = {x^2} - 2x - \frac{{10}}{9}\int\limits_0^1 {f\left( x \right) \cdot d\left( {f\left( x \right)} \right)} \)

\( = {x^2} - 2x - \left. {\frac{5}{9}{f^2}\left( x \right)} \right|_0^1 = {x^2} - 2x - \frac{5}{9}\left[ {{f^2}\left( 1 \right) - {f^2}\left( 0 \right)} \right].\)

\( \Rightarrow \left\{ \begin{array}{l}f\left( 0 \right) = - \frac{5}{9}\left[ {{f^2}\left( 1 \right) - {f^2}\left( 0 \right)} \right]\\f\left( 1 \right) = - 1 - \frac{5}{9}\left[ {{f^2}\left( 1 \right) - {f^2}\left( 0 \right)} \right]\end{array} \right.\)\( \Rightarrow f\left( 0 \right) - f\left( 1 \right) = 1 \Rightarrow f\left( 1 \right) = f\left( 0 \right) - 1 \Rightarrow f\left( 0 \right) = - \frac{5}{9}\left[ {{{\left( {f\left( 0 \right) - 1} \right)}^2} - {f^2}\left( 0 \right)} \right]\)

\( \Rightarrow f\left( 0 \right) = 5 \Rightarrow f\left( 1 \right) = 4 \Rightarrow f\left( x \right) = {x^2} - 2x + 5.\)

Phương trình hoành độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 5\) là

\({x^2} - 2x + 5 = 5 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\end{array}} \right.\).

Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = 5\) là \(\int\limits_0^2 {\left| {{x^2} - 2x + 5 - 5} \right|dx} = \frac{4}{3}{\rm{.}}\) Chọn C.

Để đồ thị hàm số \(y = \frac{{2x + 4}}{{x - m}}\) có tiệm cận đứng nằm bên trái trục tung thì

\(\left\{ {\begin{array}{*{20}{l}}{ - 2m - 4 \ne 0}\\{m < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x - m}\\{m \ne - 2}\\{m < 0}\end{array}{\rm{ m\`a }}\left\{ {\begin{array}{*{20}{l}}{m \in \mathbb{Z}}\\{m \in \left[ { - 2023\,;\,\,2023} \right]}\end{array} \Rightarrow m \in \left\{ { - 2023\,;\,\, - 2022\,;\,\, \ldots \,;\,\, - 1} \right\}\backslash \left\{ { - 2} \right\}} \right.} \right.} \right.\)

Vậy có tất cả 2022 giá trị nguyên của \(m\) thỏa mãn đề bài. Chọn C.

Gọi \(z = a + bi\,\,(a,\,b \in \mathbb{R})\).

Ta có \(3 \le \left| {z - 3i + 1} \right| \le 5 \Leftrightarrow 3 \le \left| {a + bi - 3i + 1} \right| \le 5 \Leftrightarrow 9 \le {\left( {a - 3} \right)^2} + {\left( {b + 1} \right)^2} \le 25\).

Do đó tập hợp các điểm biểu diễn của \(z\) là hình vành khăn giới hạn bởi hai đường tròn có tâm \(I\left( {3\,;\,\, - 1} \right),\) bán kính lần lượt là 3 và 5. Vì vậy \(S = \pi \left( {{5^2} - {3^2}} \right) = 16\pi .\) Chọn D.

Ta có thể tích chiếc hộp: \(V = {x^2}h = 32\) (đvtt), với \(x,\,\,h > 0.\) Suy ra \(h = \frac{{32}}{{{x^2}}}.\)

Phần mạ vàng của chiếc hộp: \(S = 2{x^2} + 8xh = 2{x^2} + 8x \cdot \frac{{32}}{{{x^2}}} = 2{x^2} + \frac{{256}}{x}.\)

Cách 1. Ta có \(2{x^2} + \frac{{256}}{x} = 2{x^2} + \frac{{128}}{x} + \frac{{128}}{x} \ge 3\sqrt[3]{{2{x^2} \cdot \frac{{128}}{x} \cdot \frac{{128}}{x}}} = 96\) (BĐT AM – GM)

Đẳng thức xảy ra khi \(2{x^2} = \frac{{128}}{x}\) hay \(x = 4\), khi đó \(h = 2.\)

Cách 2. Xét hàm số \(f\left( x \right) = 2{x^2} + \frac{{256}}{x}\) với \(x > 0\).

Ta có \(f'\left( x \right) = 4x - \frac{{256}}{{{x^2}}} = \frac{{4{x^3} - 256}}{{{x^2}}};\,\,f'\left( x \right) = 0 \Leftrightarrow 4{x^3} - 256 = 0 \Leftrightarrow x = 4\,;\,\,f\left( 4 \right) = 96.\)

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy hàm số đạt GTNN tại \(x = 4\), khi đó \(h = 2.\) Chọn A.

Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {a{x^2} + bx} - cx} \right) = - 3 \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {a - {c^2}} \right){x^2} + bx}}{{\sqrt {a{x^2} + bx} + cx}} = - 3.\)

Điều này xảy ra \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a - {c^2} = 0\,\,\left( {a,\,\,c > 0} \right)}\\{\frac{b}{{\sqrt a + c}} = - 3}\end{array}} \right.\) (vì nếu \(c \le 0\) thì \(\left. {\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {a{x^2} + bx} - cx} \right) = + \infty } \right).\)

Mặt khác, ta cũng có \({c^2} + a = 2.\) Do đó, \(\left\{ {\begin{array}{*{20}{l}}{a = {c^2} = 1}\\{b = - 3\left( {\sqrt a + c} \right) = - 6}\end{array} \Rightarrow a = 1\,,\,\,b = - 6\,,\,\,c = 1} \right..\)

Vậy \(P = a + b + 5c = 0.\) Chọn A.

Ta có \(g'\left( x \right) = {\left( {3 - x} \right)^\prime }f'\left( {3 - x} \right) + \frac{1}{6} \cdot 3 \cdot 2x \cdot {\left( {{x^2} - 1} \right)^2} = - f'\left( {3 - x} \right) + x \cdot {\left( {{x^2} - 1} \right)^2}\).

Với \(f'\left( x \right) = \left( {3 - x} \right){\left( {10 - 3x} \right)^2}{\left( {x - 2} \right)^2}\)

\[ \Rightarrow f'\left( {3 - x} \right) = \left[ {3 - \left( {3 - x} \right)} \right] \cdot {\left[ {10 - 3\left( {3 - x} \right)} \right]^2} \cdot {\left[ {\left( {3 - x} \right) - 2} \right]^2} = x \cdot {\left( {3x + 1} \right)^2} \cdot {\left( {x - 1} \right)^2}\]

Do đó \(g'\left( x \right) = - x \cdot {\left( {3x + 1} \right)^2} \cdot {\left( {x - 1} \right)^2} + x \cdot {\left( {x - 1} \right)^2} \cdot {\left( {x + 1} \right)^2}\)

\( = x \cdot {\left( {x - 1} \right)^2} \cdot \left[ { - {{\left( {3x + 1} \right)}^2} + {{\left( {x + 1} \right)}^2}} \right] = x \cdot {\left( {x - 1} \right)^2} \cdot \left( { - 8{x^2} - 4x} \right) = - {x^2} \cdot {\left( {x - 1} \right)^2} \cdot \left( {8x + 4} \right)\).

Suy ra \(g'\left( x \right) > 0 \Leftrightarrow - 8x - 4 > 0 \Leftrightarrow - 8x > 4 \Leftrightarrow x < - \frac{1}{2}.\)

Vậy hàm số đã cho đồng biến trên \(\left( { - \infty \,;\,\, - \frac{1}{2}} \right).\) Chọn D.

Mặt cầu \[\left( S \right)\] có tâm \(I\left( {1\,;\,\,1\,;\,\,1} \right)\), bán kính \(R = \sqrt 3 .\)

Ta có \(O,\,\,A \in \left( S \right)\); \(OA = 2\sqrt 2 \Rightarrow {R_{OAB}} = \frac{{OA\sqrt 3 }}{3} = \frac{{2\sqrt 6 }}{3}.\)

Gọi \(H\) là tâm tam giác đều \[OAB\].

Do \(O,\,\,A,\,\,B \in \left( S \right) \Rightarrow IH = d\left( {I,\,\,\left( {OAB} \right)} \right) = \sqrt {{R^2} - R_{OAB}^2} = \frac{{\sqrt 3 }}{3}\).

Giả sử \(\left( {OAB} \right):ax + by + cz = 0\) do

\(A \in \left( {OAB} \right) \Rightarrow 2a + 2b = 0 \Leftrightarrow a = - b \Rightarrow \left( {OAB} \right):ax - ay + cz = 0.\)

Ta có \(d\left( {I,\,\,\left( {OAB} \right)} \right) = \frac{{\left| c \right|}}{{\sqrt {2{a^2} + {c^2}} }} = \frac{{\sqrt 3 }}{3} \Leftrightarrow {a^2} = {c^2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = c}\\{a = - c}\end{array}} \right.\) .

• Với \(a = c\) chọn \(a = 1\,,\,\,c = 1 \Rightarrow (P):x - y + z = 0 \Rightarrow B\left( { - 2\,;\,\,2\,;\,\,4} \right)\) (loại).

• Với \(a = - c\) chọn \(a = 1\,,\,\,c = - 1 \Rightarrow (P):x - y - z = 0 \Rightarrow B\left( {2\,;\,\, - 2\,;\,\,4} \right)\).

Chọn B.

Ta có \(f\left( x \right)\) là hàm lẻ trên \(\mathbb{R}\). Hàm số đồng biến trên \(\mathbb{R}\).

Ta có \(f\left( {{4^x} - mx + 37m} \right) + f\left( {\left( {x - m - 37} \right) \cdot {2^x}} \right) \ge 0 \Leftrightarrow f\left( {{4^x} - mx + 37m} \right) \ge f\left( { - \left( {x - m - 37} \right) \cdot {2^x}} \right)\)

\( \Leftrightarrow {4^x} - mx + 37m \ge - \left( {x - m - 37} \right) \cdot {2^x} \Leftrightarrow {4^x} + \left( {x - m - 37} \right) \cdot {2^x} - mx + 37m \ge 0(*)\)\(f\left( {{4^x} - mx + 37m} \right) + f\left( {\left( {x - m - 37} \right) \cdot {2^x}} \right) \ge 0\) nghiệm đúng với mọi \(x \in \mathbb{R} \Leftrightarrow (*)\) nghiệm đúng với mọi \(x \in \mathbb{R}.\)

Đặt \[f\left( x \right) = {4^x} + \left( {x - m - 37} \right) \cdot {2^x} - mx + 37m \Rightarrow f'\left( x \right) = {4^x}\ln 4 + \left( {x - m - 37} \right) \cdot {2^x}\ln 2 + {2^x} - m\].

Nhận xét: \(f\left( 5 \right) = 0\). Điều kiện cần: \(f'\left( 5 \right) = 0 \Leftrightarrow m = 32\).

Điều kiện đủ: \(f\left( x \right) = {4^x} + \left( {x - 69} \right) \cdot {2^x} - 32x + 1184 = \left( {{2^x} - 32} \right)\left( {{2^x} + x - 37} \right)\)

• Nếu \(x > 5\) thì \(\left\{ {\begin{array}{*{20}{l}}{{2^x} - 32 > 0}\\{{2^x} + x - 37 > 0}\end{array} \Rightarrow f\left( x \right) > 0} \right..\)

• Nếu \(x = 5\) thì \(f\left( 5 \right) = 0\).

• Nếu \(x < 5\) thì \(\left\{ {\begin{array}{*{20}{l}}{{2^x} - 32 < 0}\\{{2^x} + x - 37 < 0}\end{array} \Rightarrow f\left( x \right) > 0} \right..\)

Vậy với \(m = 32\) thì bất phương trình đã cho có nghiệm đúng với mọi \(x \in \mathbb{R}.\) Chọn C.

Ta có \(y =  - {x^4} + 6{x^2} + mx \Rightarrow y' =  - 4{x^3} + 12x + m\).

Suy ra \(y' = 0 \Leftrightarrow  - 4{x^3} + 12x + m = 0 \Leftrightarrow m = 4{x^3} - 12x = f\left( x \right)\).

Yêu cầu bài toán \( \Leftrightarrow m = f\left( x \right)\) có 3 nghiệm đơn phân biệt.

Bảng biến thiên của \(f\left( x \right)\):

Dựa vào hình vẽ, ta được \( - 8 < m < 8\).

Đáp án: 17.

Phương trình (*) vô nghiệm thì \({x^2} + bx + c = 0\) cũng vô nghiệm.

Điều kiện: \(x \ne - 1\) không có ý nghĩa ở bài toán này.

Khi đó \(\Delta = {b^2} - 4c < 0 \Leftrightarrow {b^2} < 4c.\)

TH1: \(b = 1 \Rightarrow 4c > 1 \Leftrightarrow c > \frac{1}{4} \Rightarrow c \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6} \right\}.\) Suy ra có 6 cách gieo.

TH2: \[b = 2 \Rightarrow 4c > 4 \Leftrightarrow c > 1 \Rightarrow c \in \left\{ {2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6} \right\}.\] Suy ra có 5 cách gieo.

TH3: \(b = 3 \Rightarrow 4c > 9 \Leftrightarrow c > \frac{9}{4} \Rightarrow c \in \left\{ {3\,;\,\,4\,;\,\,5\,;\,\,6} \right\}.\) Suy ra có 4 cách gieo.

TH4: \(b = 4 \Rightarrow 4c > 16 \Leftrightarrow c > 4 \Rightarrow c \in \left\{ {5\,;\,\,6} \right\}.\) Suy ra có 2 cách gieo.

TH5: \(b = 5 \Rightarrow 4c > 25 \Leftrightarrow c > \frac{{25}}{4} \Rightarrow c \in \emptyset .\)

Vậy xác suất cần tìm là \(P = \frac{{6 + 5 + 4 + 2}}{{6.6}} = \frac{{17}}{{36}}.\)

Đáp án: \(\frac{{17}}{{36}}.\)

Đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\) đi qua gốc tọa độ \(O\left( {0\,;\,\,0} \right)\) nên \(c = 0.\)

Suy ra công thức hàm số là \(a{x^2} + bx.\)

Mặt khác đồ thị hàm số qua hai điểm \(A\left( {43\,;\,\,0} \right),\,\,B\left( {0,2\,;\,\,1,87} \right)\) nên ta có hệ phương trình:

\[\left\{ {\begin{array}{*{20}{l}}{a \cdot {{\left( {0,2} \right)}^2} + b \cdot 0,2 = 1,87}\\{a \cdot {{43}^2} + b \cdot 43 = 0}\end{array}} \right.\]

Suy ra \(a = - \frac{{187}}{{856}};\,\,b = \frac{{8041}}{{856}}\) nên có hàm số \(y = - \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x.\)

Hình chiếu của đỉnh \(S\) trên trục hoành là \(H\) nên

\({y_S} = f\left( {{x_S}} \right) = f\left( {{x_H}} \right) = f\left( {\frac{{{x_A}}}{2}} \right) = f\left( {\frac{{43}}{2}} \right) \approx 101\,\,(m).\)

Vậy độ cao từ đỉnh vòm phia trong một trụ của cầu Nhật Tân tới mặt đường là khoảng \(101\;\,\,{\rm{m}}.\)

Đáp án: 101.

Xét hàm số \(y = f\left( {{x^2} + 1} \right)\) có \(y' = 2x \cdot f'\left( {{x^2} + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{f'\left( {{x^2} + 1} \right) = 0}\end{array}} \right.\).

Dựa vào hình vẽ, ta thấy \(f'\left( x \right) = 0 \Leftrightarrow x \in \left\{ {1\,;\,\,3\,;\,\,4} \right\}\) (loại nghiệm kép \(x = 2\))

Khi đó \(f'\left( {{x^2} + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} + 1 = 1}\\{{x^2} + 1 = 3}\\{{x^2} + 1 = 4}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} = 0}\\{{x^2} = 2}\\{{x^2} = 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x =  \pm \sqrt 2 .}\\{x =  \pm \sqrt 3 }\end{array}} \right.} \right.} \right.\)

Bảng biến thiên của \(f\left( {{x^2} + 1} \right)\):

Dựa vào hình vẽ, ta thấy \(f\left( {{x^2} + 1} \right) = f\left( 3 \right)\) có tất cả 4 nghiệm phân biệt.

Đặt \(\mathop {\lim }\limits_{x \to 3} \frac{{f\left( x \right) - 15}}{{x - 3}} = g\left( x \right) \Rightarrow f\left( x \right) = \left( {x - 3} \right)g\left( x \right) + 15 \Rightarrow \mathop {\lim f\left( x \right) = 15}\limits_{x \to 3} \).

Khi đó \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt[3]{{5f\left( x \right) - 11}} - 4}}{{{x^2} - x - 6}} = \mathop {\lim }\limits_{x \to 3} \frac{{5f\left( x \right) - 11 - 64}}{{{{\left( {\sqrt[3]{{5f\left( x \right) - 11}}} \right)}^2} + 4\sqrt[3]{{5f\left( x \right) - 11}} + 16}} \cdot \frac{1}{{\left( {x - 3} \right)\left( {x + 2} \right)}}\)

 \( = \mathop {\lim }\limits_{x \to 3} \frac{{5\left[ {f\left( x \right) - 15} \right]}}{{x - 3}} \cdot \frac{1}{{\left( {x + 2} \right)\left[ {{{\left( {\sqrt[3]{{5f\left( x \right) - 11}}} \right)}^2} + 4\sqrt[3]{{5f\left( x \right) - 11}} + 16} \right]}}\)\( = 5 \cdot 12 \cdot \frac{1}{{5 \cdot \left[ {16 + 16 + 16} \right]}} = \frac{1}{4}.\)

Đáp án: \(\frac{1}{4}.\)

Ta có điểm biểu diễn \(z\) là \(M\left( {x\,;\,\,y} \right).\)

• Với \(m = 0\), ta có \(z = 0\), thỏa mãn yêu cầu bài toán.

• Với \(m > 0\):

− Tập hợp điểm biểu diễn của số phức \(z\) thỏa mãn \(\left| z \right| = m\) đường tròn \(\left( {{C_1}} \right)\) tâm \(I\left( {0\,;\,\,0} \right)\) bán kính \(R = m\)

− Tập hợp điểm biểu diễn của số phức \(z\) thỏa mãn \(\left| {z - 4m + 3mi} \right| = {m^2}\)

\( \Leftrightarrow {\left( {x - 4m} \right)^2} + {\left( {y + 3m} \right)^2} = {m^4}\) nên \(M\) thuộc đường tròn \(\left( {{C_2}} \right)\) tâm \(I'\left( {4m\,;\,\, - 3m} \right)\), bán kính \(R' = {m^2}.\)

Có duy nhất một số phức \(z\) thỏa mãn yêu cầu bài toán khi và chỉ khi \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc nhau

\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{OI = R + R'}\\{OI' = \left| {R - R'} \right|}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{5m = {m^2} + m}\\{5m = \left| {{m^2} - m} \right|}\\{m > 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 4}\\{m = 6}\end{array}.} \right.} \right.}\end{array}} \right.\)

Kết hợp với \(m = 0\), suy ra \(m \in \left\{ {0\,;\,\,4\,;\,\,6} \right\}.\) Vậy tổng tất cả các giá trị của \(m\) là 10.

Đáp án: 10.

Ta có \({\log _x}y + 6{\log _y}x = 5 \Leftrightarrow {\log _x}y + \frac{6}{{{{\log }_x}y}} = 5 \Leftrightarrow {\left( {{{\log }_x}y} \right)^2} - 5{\log _x}y + 6 = 0\)

TH1: \({\log _x}y = 2 \Leftrightarrow y = {x^2} \in \left[ {2\,;\,\,2021} \right] \Leftrightarrow 2 \le {x^2} \le 2021 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt 2 \le x \le \sqrt {2021} }\\{ - \sqrt {2021} \le x \le - \sqrt 2 }\end{array}} \right..\)

Kết hợp với điều kiện: \(2 \le x \le 2020\) và \(x \in \mathbb{Z} \Rightarrow \) có 43 cặp số nguyên \(\left( {x\,;\,\,y} \right)\).

TH2: \({\log _x}y = 3 \Leftrightarrow y = {x^3} \in \left[ {2\,;\,\,2021} \right] \Leftrightarrow 2 \le {x^3} \le 2021 \Leftrightarrow \sqrt[3]{2} \le x \le \sqrt[3]{{2021}}\)

Kết hợp với điều kiện: \(2 \le x \le 2020\) và \(x \in \mathbb{Z} \Rightarrow \) có 11 cặp số nguyên \(\left( {x\,;\,\,y} \right)\).

Vậy có tất cả \(43 + 11 = 54\) cặp số nguyên \(\left( {x\,;\,\,y} \right)\).

Đáp án: 54.

Ta có \(i \cdot \bar w = \left( {3 - 4i} \right)z + 2i \Leftrightarrow \left( {3 - 4i} \right)z = i \cdot \bar w - 2i \Leftrightarrow z = \frac{{i \cdot \bar w - 2i}}{{3 - 4i}}\)

\( \Leftrightarrow \left| z \right| = \left| {\frac{{i \cdot \bar w - 2i}}{{3 - 4i}}} \right| \Leftrightarrow \left| {\frac{{i \cdot \left( {\bar w - 2} \right)}}{{3 - 4i}}} \right| = 2 \Leftrightarrow \frac{{\left| i \right| \cdot \left| {\bar w - 2} \right|}}{{\left| {3 - 4i} \right|}} = 2\)\( \Leftrightarrow \left| {\bar w - 2} \right| = 10 \Leftrightarrow \left| {w - 2} \right| = 10.\)

Vậy tập hợp điểm biểu diễn các số phức \(w\) là đường tròn có bán kính bằng 10.

Đáp án: 10.

Gọi \(I\) là điểm thỏa mãn: \(IA - 2IB = 0 \Rightarrow I\left( { - 4\,;\,\,3\,;\,\, - 2} \right).\)

Khi đó \(T = M{A^2} - 2M{B^2} = - M{I^2} + I{A^2} - 2I{B^2} \Rightarrow {T_{\max }} \Leftrightarrow M{I_{\min }}\)

\( \Leftrightarrow M\) là hình chiếu của \(I\) lên mặt phẳng \(\left( P \right).\)

Khi đó đường thẳng \[MI\] đi qua \(I\left( { - 4\,;\,\,3\,;\,\, - 2} \right)\) và vuông góc với \(\left( P \right)\) nên nhận vectơ pháp tuyến \[\vec n\left( {5\,;\,\, - 1\,;\,\,1} \right)\] của \(\left( P \right)\) làm vectơ chỉ phương, phương trình là \(\left\{ {\begin{array}{*{20}{l}}{x = - 4 + 5t}\\{y = 3 - t}\\{z = - 2 + t}\end{array}\,\,\,\left( {t \in \mathbb{R}} \right)} \right..\)

Ta có \(M = IM \cap \left( P \right) \Rightarrow \) Tọa độ \(M\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{l}}{x = - 4 + 5t}\\{y = 3 - t}\\{z = - 2 + t}\\{5x - y + z - 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t = 1}\\{x = 1}\\{y = 2}\\{z = - 1}\end{array}} \right.} \right.\)

Do đó \(M\left( {1\,;\,\,2\,;\,\, - 1} \right) \Rightarrow {x_M} = 1.\)

Đáp án: 1.

Ta có \({a^x} = {b^y} = \sqrt {ab} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {{\log }_a}\sqrt {ab} = \frac{1}{2}{{\log }_a}\left( {ab} \right) = \frac{1}{2} + \frac{1}{2}{{\log }_a}b}\\{y = {{\log }_b}\sqrt {ab} = \frac{1}{2}{{\log }_b}\left( {ab} \right) = \frac{1}{2} + \frac{1}{2}{{\log }_b}a}\end{array}} \right.\)

Đặt \(X = {\log _a}b > 0\), khi đó \(P = x + 2y = \frac{1}{2} + \frac{1}{2}X + 2 \cdot \left( {\frac{1}{2} + \frac{1}{2} \cdot \frac{1}{X}} \right)\)

\( = \frac{1}{2} + \frac{1}{2}X + 1 + \frac{1}{X} = \left( {\frac{X}{2} + \frac{1}{X}} \right) + \frac{3}{2} \ge 2\sqrt {\frac{X}{2} \cdot \frac{1}{X}} + \frac{3}{2} = \sqrt 2 + \frac{3}{2}{\rm{. }}\)

Vậy giá trị nhỏ nhất của \(P\) là \(\sqrt 2 + \frac{3}{2} \approx 3.\)

Đáp án: 3.

Giải thích: “Săn bắt” là hành động con người sử dụng các công cụ lao động nhằm săn và bắt các con thú. Đại bàng là động vật, không thể thực hiện hành động này. Chọn B.

Từ “nhiễm” (bị yếu tố bên ngoài thường là độc hại xâm nhập vào gây ra những hậu quả xấu) dùng chưa hợp lí trong ngữ cảnh câu văn. Chọn C.

“Biệt đãi” là đối xử đặc biệt, biểu thị thái độ rất coi trọng nên sử dụng từ “bị” trước đó là không phù hợp. Chọn A.

Từ “xâm nhập” dùng sai vì “xâm nhập” có nghĩa là đi vào một cách trái phép, thường gây ra tác hại. Nên thay “xâm nhập” bằng “thâm nhập” (đi sâu vào và cùng hoà mình trong một môi trường hoạt động nào đó). Chọn C.

Từ có nghĩa không giống các từ còn lại là “học tập”. “Học vẹt, học gạo, học vần” là các kiểu và các cách học. “Học vẹt” là học bằng cách bắt chước y hệt không quan tâm đến nội dung, “học gạo” là học bằng cách nhồi nhét kiến thức thuần túy, “học vần” là học đánh vần. “Học tập” là học nói chung. Chọn C.

Từ “quả” trong “quả cam” dùng với nghĩa gốc, các từ còn lại dùng với nghĩa chuyển. Chọn A.

Từ “trăng trắng” mang tính chất giảm nhẹ mức độ, tính chất. Các từ còn lại mang tính chất tăng dần về mức độ, tính chất. Chọn B.

Từ “kéo” chỉ hành động làm cho vật di chuyển lại gần. Các từ “quăng, quẳng, lia” chỉ hành động làm cho vật di chuyển ra xa. Chọn D.

Từ “mênh mông” là từ tượng hình. Các từ còn lại đều là từ tượng thanh. Chọn B.

Chí Phèo thể hiện tài năng truyện ngắn bậc thầy của Nam Cao: xây dựng thành công những nhân vật điển hình bất hủ; nghệ thuật trần thuật linh hoạt, tự nhiên mà vẫn nhất quán, chặt chẽ; ngôn ngữ nghệ thuật đặc sắc. Chọn A.

Chúng ta có trách nhiệm bảo tồn và phát huy vẻ đẹp truyền thống của văn hóa dân tộc. Chọn B.

“xanh xao” là từ chỉ màu sắc của da người. Các từ còn lại không dùng để miêu tả màu sắc của da người. Chọn C.

Từ “chống cự”: đánh trả lại để tự vệ phù hợp để điền vào chỗ trống. Chọn A.

Người chiến sĩ hi sinh anh dũng ấy nay đã được đưa về với đất mẹ quê hương. Chọn D.

Điệp từ “nắng”. Chọn C.

Nghị luận là phương thức biểu đạt chính của đoạn trích. Chọn D.

Cảm xúc mong mỏi của nhân vật trữ tình được thể hiện qua 2 dòng thơ cuối. Chọn A.

Nhân vật được đề cập đến trong đoạn trích là Phan Châu Trinh. Chọn B.

Đoạn văn quy nạp, câu chủ đề ở cuối đoạn “Chính người phụ nữ là người chăm sóc và giáo dục con cái chủ yếu trong gia đình”. Chọn B.

Từ “đặng” đồng nghĩa với từ “để”. Chọn C.

Điệp từ “Nỗi nhớ”, “nhớ”. Chọn A.

Về điển tích, Hoàng Sào trước là một anh hùng, nhưng sự nghiệp không bền vì hiếu sát, làm mất lòng dân và tướng sĩ, từ anh hùng trở thành giặc loạn, nên Kiều khuyên Từ “nghìn năm ai có khen đâu Hoàng Sào!”. Chọn A.

Các địa danh xuất hiện trong đoạn trích gắn với những trò chơi, niềm vui tuổi thơ của nhân vật trữ tình: ra cống Na câu cá, đi chợ Bình Lâm, bắt chim sẻ ở vành tai tượng Phật, ăn trộm nhãn chùa Trần, lên chơi đền Cây Thị, xem lễ đền Sòng,… Chọn B.

Thông điệp gửi qua đoạn trích: Cần lựa chọn cái đẹp đích thực để phù hợp với văn hóa. Chọn A.

Chính âm thanh tiếng sáo đã đánh thức Mị nhớ về quá khứ, nhớ lại những giai điệu ngọt ngào từ thuở xa xôi. Bằng cách trở về với quá khứ đã thổi bùng lên trong lòng Mị khát vọng tình yêu, khát vọng tuổi trẻ, kí ức về quá khứ tươi đẹp một thời đã “có biết bao nhiêu người mê, ngày đêm đã thổi sáo đi theo Mị”. Chọn B.

Hình ảnh “củi một cành khô lạc mấy dòng” là hình ảnh ẩn dụ gợi nỗi buồn về kiếp người nhỏ bé vô định. Chọn B.

Biện pháp nhân hóa và so sánh:

+ Nhân hóa được thể hiện qua các từ ngữ: chuyển hướng, vòng qua, vẽ một hình cung, ôm lấy, xuôi dần,...

+ So sánh được thể hiện qua các câu văn: và từ đó nó trôi đi giữa hai dãy đồi sừng sững như thành quách, người ta luôn luôn nhìn thấy dòng sông mềm như tấm lụa, với những chiếc thuyền xuôi ngược chỉ bé vừa bằng con thoi.

→ Chọn A.

Đoạn trích kể lại việc hai chị em Chiến và Việt khiêng bàn thờ má sang gửi nhờ nhà chú Năm. Chọn D.

Địa chủ và nông dân là giai cấp cũ trong xã hội. Công nhân là giai cấp mới được hình thành trong cuộc khai thác thuộc địa lần thứ nhất của thực dân Pháp. Chọn D.

Hội Quốc liên ra đời để duy trì trật tự thế giới sau Chiến tranh thế giới thứ nhất. Chọn B.

Với kế hoạch Mácsan (6-1947), Mĩ đã viện trợ cho Tây Âu 17 tỷ đô la giúp Tây Âu khôi phục kinh tế. Kế hoạch Mácsan của Mĩ đã tạo nên sự đối lập về kinh tế và chính trị giữa các nước Tây Âu tư bản chủ nghĩa và các nước Đông Âu xã hội chủ nghĩa. Đây chính là mục đích hàng đầu của Mĩ khi thực hiện kế hoạch Mácsan để tạo lập đồng minh quân sự chống lại Liên Xô và Đông Âu. Chọn A.

Một đặc điểm lớn của tình hình thế giới sau Chiến tranh lạnh là sự điều chỉnh quan hệ giữa các nước lớn theo chiều hướng đối thoại, thỏa hiệp, tránh xung đột trực tiếp. Chọn B.

Năm 1949, Liên Xô chế tạo thành công bom nguyên tử, phá vỡ thế độc quyển bom nguyên tử của Mĩ. Chọn D.

Tình trạng đối đầu hai cực Xô-Mĩ là do sự đối lập nhau về mục tiêu và chiến lược giữa hai quốc gia và không chịu sự tác động của cuộc cách mạng khoa học-kĩ thuật lần thứ hai. Chọn A.

Vào giữa thế kỷ XIX, Việt Nam bị cô lập với thế giới bên ngoài chủ yếu là do chính sách “bế quan tỏa cảng” của nhà Nguyễn. Chọn B.

Sau Chiến tranh thế giới thứ hai, Mĩ và các nước Tây Âu thành lập khối quân sự NATO nhằm mục đích chống lại Liên Xô và các nước xã hội chủ nghĩa ở Đông Âu. Chọn D.

Hoa Kì nằm giữa Thái Bình Dương và Đại Tây Dương → Nhận định Hoa Kì nằm giữa Ấn Độ Dương và Đại Tây Dương là sai. Chọn D.

Trung Quốc đã sử dụng lực lượng lao động dồi dào ở địa bàn nông thôn để phát triển ngành dệt may (SGK/94 Địa lí 11). Chọn A.

Phân tích nội dung các đáp án, ta thấy:

- A sai: mùa bão diễn ra từ tháng 6-12

- B sai: bão không chỉ hình thành trên biển Đông, có những cơn bão xuất phát từ vùng biển phía Nam hoặc phía Bắc

- C sai: các cơn bão đổ bổ bộ nhiều nhất vào miền Trung nước ta, miền Nam cũng chịu ảnh hưởng của bão nhưng ít hơn và đến muộn hơn.

- D đúng: mùa bão chậm dần từ Bắc vào Nam. Chọn D.

Nơi có nhiệt độ cao, nhiều nắng, it sông đổ ra biển thuận lợi nhất cho nghề làm muối vì có độ bốc hơi cao, độ mặn cao. Chọn B.

Điện Biên Phủ, Hà Giang, Tuyên Quang. Chọn A.

Cơ cấu + 1 mốc thời gian → Biểu đồ tròn. Chọn C.

Các nhà máy nhiệt điện chạy bằng than không phát triển ở phía Nam chủ yếu là do xa nguồn nguyên liệu than chứ không phải vì lý do nào khác. Chọn A.

Thế mạnh nông nghiệp nhiệt đới ở trung du và miền núi nước ta là cây công nghiệp lâu năm (cà phê, cao su, chè, hồ tiêu, điều…) và chăn nuôi gia súc lớn trên các đồng cỏ (trâu, bò). Chọn A.

Cà phê là cây trồng quan trọng nhất của Tây Nguyên. Chọn D.

Giá trị nông sản nói chung, thuỷ sản nói riêng được nâng cao khi làm chủ được khâu chế biến. Mặt khác, việc xuất khẩu thuỷ sản thu lại lợi nhuận lớn. Chọn A.

Ở điều kiện bình thường, chất khí không dẫn điện. → A sai

Tia sét là dòng điện tự lực trong chất khí khi không khí chịu tác dụng của điện trường cực mạnh đến mức bị ion hoá → B sai

Tia lửa điện và hồ quang điện là hai dạng phóng điện tự lực trong chất khí có cùng điều kiện xuất hiện → C sai

Chọn D.

Cảm ứng từ tại điểm \({\rm{M}}\) có độ lớn là \(B = {2.10^{ - 7}} \cdot \frac{I}{r} = \frac{{{{2.10}^{ - 7}}.1}}{{0,1}} = {2.10^{ - 6}}\;{\rm{T}}\). Chọn C.

Ta có: \(\frac{d}{{d'}} = \frac{{OA}}{{OA'}} = \frac{2}{3} \Rightarrow \frac{{20}}{{d'}} = \frac{2}{3} \Rightarrow d' = 30\;{\rm{cm}}\)

Tiêu cự của thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow f = 12\;{\rm{cm}}\)

Chọn D.

Người thợ cơ khí khi hàn điện thường sử dụng kính bảo vệ. Tấm kính bảo vệ có tác dụng chủ yếu là hấp thụ ánh sáng tử ngoại phát ra từ mối hàn đến mắt. Chọn C.

Theo thuyết lượng tử ánh sáng, ánh sáng được tạo thành bởi các hạt photon. Chọn C.

\({\beta ^ + }\) hay e \(^ + \)là các pozitron, hay electron dương, có cùng khối lượng với electron nhưng mang điện tích dương. Chọn A

\(\omega = \frac{{{V_M}}}{A} = \frac{{{I_0}}}{{{Q_0}}}.\) Chọn A.

Công thức tính chu kì con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \Leftrightarrow {T^2} = \frac{{4{\pi ^2}}}{k} \cdot m\)

\( \Rightarrow \) Đồ thị T theo m có dạng parabol có bề lõm hướng theo chiều dương trục Om. Chọn hình 2.

Chọn D.

Nhận thấy: \({U^2} + U_X^2 = U_Y^2 \Rightarrow \overrightarrow U \bot \overrightarrow {{U_X}} \)

\( \Rightarrow \) Phần tử X và Y là cuộn dây không thuần cảm và tụ điện. Chọn A.

Khi sử dụng bức xạ màu vàng: \(MN = 12{i_1} = 12\frac{{{\lambda _1}D}}{a} \Rightarrow {x_M} = - {x_N} = 6\frac{{{\lambda _1}D}}{a}\)

Khi sử dụng bức xạ màu xanh: \( - 6\frac{{{\lambda _1}D}}{a} \le n{i_2} \le 6\frac{{{\lambda _1}D}}{a} \Leftrightarrow - 6{\lambda _1} \le n{\lambda _2} \le 6{\lambda _1} \Leftrightarrow - 7,2 \le n \le 7,2\)

Có 15 giá trị của n nguyên. Có 15 vân sáng.

Đáp án: 15.

\({{\rm{n}}_{\rm{x}}} = 0,8\;\)mol; \({{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}} = 0,6\;\)mol; \({{\rm{n}}_{{\rm{alkane }}}} = {{\rm{n}}_{alkene}} = \frac{{0,8}}{4} = 0,2\;\)mol; \({{\rm{n}}_{alkyne}} = 0,4\;\)mol

Khi cho X qua bình đựng dung dịch \[AgN{O_3}/N{H_3}\] lấy dư thu được 96 gam kết tủa.

TH1: Alkyne là \[{C_2}{H_2}.\]

\(\begin{array}{l}{\rm{HC}} \equiv {\rm{CH}} + 2{\rm{AgN}}{{\rm{O}}_3} + 2{\rm{N}}{{\rm{H}}_3} \to {\rm{AgC}} \equiv {\rm{CAg}} + 2{\rm{N}}{{\rm{H}}_4}{\rm{N}}{{\rm{O}}_3}\\{{\rm{n}}_{{{\rm{C}}_2}{{\rm{H}}_2}}} = {{\rm{n}}_{{{\rm{C}}_2}{\rm{A}}{{\rm{g}}_2}}} = \frac{{96}}{{240}} = 0,4\;{\rm{mol}} = {{\rm{n}}_{alkyne\,\,\,({\rm{x}})}}\end{array}\)

Đốt cháy Y gồm: 0,2 mol alkane và 0,2 mol alkene sẽ thu được:

\({n_{alkane}} = {n_{{H_2}O}} - {n_{C{O_2}}} \to {n_{{H_2}O}} = {n_{alkane}} + {n_{C{O_2}}} = 0,8\,mol\)

\(\begin{array}{l} \Rightarrow {m_Y} = {m_C} + {m_H} = 0,6 \cdot 12 + 0,8 \cdot 2 = 8,8\,gam\\ \Rightarrow {m_X} = {m_y} + {m_{{C_2}{H_2}}} = 8,8 + 0,4 \cdot 26 = 19,2\,gam.\end{array}\)

TH2: Alkyne có dạng \({\rm{RC}} \equiv {\rm{CH}}\) (R khác H).

\(\begin{array}{l}{\rm{RC}} \equiv {\rm{CH}} + {\rm{AgN}}{{\rm{O}}_3} + {\rm{N}}{{\rm{H}}_3} \to {\rm{RC}} \equiv {\rm{CAg}} + {\rm{N}}{{\rm{H}}_4}{\rm{N}}{{\rm{O}}_3}\\\;\,\,\,\,\,\,0,4{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\,\,\,\,0,4{\rm{ }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

\({{\rm{M}}_{RC \equiv CAg}} = \frac{{96}}{{0,4}} = 240 \Rightarrow {\rm{R}} = 108\)(loại).

Chọn A.

\(HCl + \left\{ \begin{array}{l}CO_3^{2 - }:0,15\,mol\\HCO_3^ - :0,1\,mol\\N{a^ + }:0,3\,mol\\{K^ + }:0,1\,mol\end{array} \right.\)

Khi cho từ từ HCl vào dung dịch \(N{a_2}C{O_3},KHC{O_3}\)xảy ra các quá trình sau:

\(\begin{array}{l}{H^ + } + CO_3^{2 - } \to HCO_3^ - \\0,15\,\,\,0,15\,\,\,\,\,\,\,\,\,0,15\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

Sau quá trình này tổng số mol \(HCO_3^ - \)là 0,25 mol

\(\begin{array}{l}{H^ + } + HCO_3^ - \to C{O_2} + {H_2}O\\0,25\,\,0,25\,\,\,\,\,\,\,\,\,\,\,\,\,0,25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

Dựa vào đồ thị các phản ứng hoá học trên ta suy ra

+) b là số mol \[C{O_2}\]tối đa thu được: b = 0,25

+) a là số mol \[C{O_2}\] sinh ra khi lượng HCl thêm vào là 0,2 mol: a = 0,2 – 0,15 = 0,05

Þ a + b = 0,25 + 0,05 = 0,3.

Chọn B.

- TN1: khí là \({\rm{N}}{{\rm{H}}_3}.\)

- TN2: khí là \({\rm{C}}{{\rm{O}}_2} \Rightarrow \) loại B và C (vì \({V_1} = {V_2}\) ).

- TN3: sinh khí \( \Rightarrow {\rm{X}},{\rm{Y}}\) chứa \({{\rm{H}}^ + } \Rightarrow \) A đúng.

Chọn A.

\({\rm{X}}\) có dạng \({{\rm{H}}_2}{\rm{NR}}{({\rm{COOH}})_b}\)

- 50 mL dung dịch \({\rm{X}} + 0,04\;{\rm{mol}}\,\,{\rm{HCl}} \Rightarrow \) dung dịch phản ứng vừa đủ với \(0,08\;{\rm{mol}}\,\,{\rm{NaOH}}\).

Lượng\({\rm{NaOH}}\)trung hòa dung dịch thu được = lượng \({\rm{NaOH}}\)trung hòa dung dịch \({\rm{X}}\) và \(0,04\;{\rm{mol}}\,\,{\rm{HCl}}\) \( \Rightarrow {\rm{b}} \cdot {{\rm{n}}_{\rm{X}}} + 0,04 = 0,08 \Rightarrow {\rm{b}} \cdot {{\rm{n}}_{\rm{X}}} = 0,04\,mol\)

- 250 mL dung dịch \({{\rm{H}}_2}{\rm{NR}}{({\rm{COOH}})_b} + {\rm{KOH}} \to 40,6\) gam \({{\rm{H}}_2}{\rm{NR}}{({\rm{COOK}})_b} + {{\rm{H}}_2}{\rm{O}}\)

\({n_X} = 5 \cdot \frac{{0,04}}{b} = \frac{{0,2}}{b}\;{\rm{mol}}\).

\( \Rightarrow {{\rm{n}}_{{{\rm{H}}_2}{\rm{NR}}{{({\rm{COOK}})}_{\rm{b}}}}} = {{\rm{n}}_{\rm{X}}} = \frac{{0,2}}{{\rm{b}}}\) mol.

\[\begin{array}{l}{M_{{H_2}{\rm{NR(COOK}}{{\rm{)}}_b}{\rm{ }}}} = 16 + {M_R} + 83b = \frac{{40,6}}{{\frac{{0,2}}{b}}} = 203b\\ \Rightarrow 16 + {M_M} = 120b \to \left\{ \begin{array}{l}b = 1\\{M_R} = 104\end{array} \right.\\ \Rightarrow R:\,\, - {C_8}{H_8} - \end{array}\]

CTPT của X là \({C_9}{H_{11}}{O_2}N.\)

Mà X là \(\alpha \)-amino acid có chứa một vòng thơm nên các CTCT tối đa thỏa mãn X là 5.

Chọn D.

Các phát biểu đúng là: (b), (c), (d), (e).

Phát biểu (a) không đúng vì chất rắn nổi lên là muối của sodium với acid béo.

Chọn A.

Tên polymer = poly + tên monomer Þ monomer là styrene.

Phương trình trùng hợp như sau:

Chọn B.

\({\mathop{\rm BTNT}\nolimits} ({\rm{N}})\) ta có \({{\rm{n}}_{{\rm{N}}{{\rm{H}}_3}}} = {{\rm{n}}_{{\rm{HN}}{{\rm{O}}_3}}} = 2\,\,(\;{\rm{mol}})\)

 $\begin{array}{l}4{\text{NH}}_3+5{\text{O}}_2\stackrel{Pt,t^{°}}{\to }4\text{NO}+6{\text{H}}_2\text{O}\\ 2\to 2,5 2mol\end{array}$

\(\begin{array}{l}2{\rm{NO}} + {{\rm{O}}_2} \to 2{\rm{N}}{{\rm{O}}_2}\\2\,\,\,\,\, \to \,\,\,\,1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

\(\begin{array}{l}4{\rm{N}}{{\rm{O}}_2} + {{\rm{O}}_2} + 2{{\rm{H}}_2}{\rm{O}} \to 4{\rm{HN}}{{\rm{O}}_3}\\2\,\,\,\, \to \,\,\,\,\,0,5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,mol\end{array}\)

\({n_{{O_2}}}\)ban đầu = a – 2 (mol)

Chọn C.

Chất không dẫn điện là do trong dung dịch không có các ion mang điện trái dấu hay nói cách khác là chất không điện li.

\(C{H_3}OH\)là chất không điện li.

Chọn B.

Ta có: \({{\rm{n}}_{{\rm{OH}}({\rm{T}})}} = 2.{{\rm{n}}_{{{\rm{H}}_2}}} = 2.\frac{{1,3635}}{{24,79}} = 0,11 = {{\rm{n}}_{{\rm{C}}{{\rm{O}}_2}}}\)

=> Trong T các alcohol có số nhóm OH bằng số C.

Lại có \({{\rm{M}}_{\rm{x}}} < {{\rm{M}}_{\rm{Y}}} < 120\) Þ T gồm \[C{H_3}OH\](x mol) và \[{C_2}{H_4}{\left( {OH} \right)_2}\](y mol).

 $\begin{array}{l}\stackrel{BTNTO}{\to }{n}_{OH\left(T\right)}+2n_{O_2}=n_{H_{2}O}+2n_{C{O}_2}\\ \Rightarrow n_{H_{2}O}=0,11+0,15\cdot 2-2\cdot 0,11=0,19mol\\ \Rightarrow n_{alcohol}=n_{H_{2}O}-n_{C{O}_2}=0,19-0,11=0,08mol\end{array}$

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x + 2y = 0,11}\\{x + y = 0,08}\end{array} \to \left\{ {\begin{array}{*{20}{l}}{x = 0,05}\\{y = 0,03}\end{array}} \right.} \right.(mol)\)

E gồm 2 ester mạch hở X và Y\(\left( {{M_X} < {M_Y} < 120} \right)\)và sau khi tác dụng với NaOH chỉ thu được 1 muối Z nên 2 ester này tạo bởi cùng một carboxylic acid.

=> Y là \[{\left( {HCOO} \right)_2}{C_2}{H_4}\](0,03 mol) và X là \[HCOOC{H_3}\](0,05 mol).

Phần trăm khối lượng của Y trong E là:

\(\% {m_Y} = \frac{{0,03.118}}{{0,03.118 + 60.0,05}}.100\% = 54,13\% \).

Đáp án: 54,13%

A. Sai. Pha tối của quang hợp diễn ra không cần sự tham gia trực tiếp của ánh sáng chứ không phải chỉ diễn ra trong điều kiện không có ánh sáng.

B. Sai. Điểm bù CO₂ của thực vật C₄ thấp hơn thực vât C₃.

C. Đúng. Nguyên liệu của quá trình quang hợp là CO₂ và H₂O.

D. Sai. Pha sáng của quang hợp sử dụng năng lượng ánh sáng để tổng hợp ATP và NADPH cung cấp cho pha tối để tổng hợp glucôzơ.

Chọn C.

Có 2 phát biểu đúng là III và IV. Chọn B.

I. Sai. Không phải tất cả các loài động vật có xương sống đều phát triển không qua biến thái, ví dụ ếch nhái trải qua biến thái hoàn toàn.

II. Sai. Không phải tất cả các loài động vật không xương sống đều phát triển qua biến thái, ví dụ giun đất không trải qua biến thái.

Cơ sở sinh học của biện pháp sử dụng bao cao su khi quan hệ tình dục là ngăn cản không cho tinh trùng xâm nhập vào tử cung để có cơ hội gặp trứng. Chọn B.

- Đột biến cấu trúc NST sẽ làm thay đổi cấu trúc NST. Trong các dạng đột biến trên thì chuyển đoạn là đột biến cấu trúc NST. Chọn B.

- Các dạng đột biến còn lại gồm lệch bội, đa bội, dị đa bội là các dạng đột biến số lượng NST nên không làm thay đổi cấu trúc NST.

D. Đúng. Quần thể ngẫu phối tạo ra một lượng biến dị di truyền rất lớn trong quần thể, duy trì được tần số các kiểu gen khác nhau không đổi trong điều kiện nhất định → duy trì được sự đa dạng di truyền của quần thể. Chọn D.

Quy trình tạo thể đột biến có kiểu gen aa có khả năng kháng bệnh theo thứ tự là: Xử lí hạt giống bằng tia phóng xạ để gây đột biến rồi gieo mọc thành cây (I) → Cho các cây con nhiễm tác nhân gây bệnh (IV) → Chọn lọc các cây có khả năng kháng bệnh (II) → Cho các cây kháng bệnh tự thụ phấn đề tạo dòng thuần (III). Chọn A.

Khó khăn khi nghiên cứu di truyền học người là: Số lượng NST lớn, kích thước nhỏ, cấu trúc của vật chất di truyền ở mức phân tử phức tạp, có nhiều vấn đề chưa được biết một cách tường tận; Thời gian chín sinh dục muộn, thời gian mang thai dài và ít con; Các vấn đề đạo đức và xã hội.

B. Sai. Các tính trạng trên cơ thể người vẫn tuân theo các quy luật di truyền. Chọn B.

Các cá thể trong loài luôn bắt cặp đúng, không có sự giao phối khác loài → Cách li trước hợp tử. Các loài không giao phối với nhau vì có tiếng kêu khác nhau → Cách li tập tính. Chọn B.

Dựa vào hình minh họa, ta thấy:

+ Ở quần thể (a), các cá thể tập hợp thành các nhóm nhỏ trong khu vực sống nên đây là kiểu phân bố theo nhóm. Mật độ cá thể của quần thể ở đây là 29 cá thể / 100 m².

+ Ở quần thể (b), các cá thể không sống tập trung mà phân bố đều trong khu vực sống nên đây là kiểu phân bố đồng đều. Mật độ cá thể của quần thể ở đây là 18 cá thể / 100 m².

+ Ở quần thể (c), các cá thể phân bố một cách ngẫu nhiên trong khu vực sống nên đây là kiểu phân bố ngẫu nhiên. Mật độ cá thể của quần thể ở đây là 24 cá thể / 100 m².

Xét sự đúng – sai của các phát biểu:

I. Sai. Mật độ cá thể của quần thể tăng dần theo thứ tự (b) → (c) → (a).

II. Sai. Phân bố theo nhóm (kiểu phân bố của quần thể a) mới là kiểu phân bố phổ biến nhất trong tự nhiên.

III. Đúng. Nếu có một số cá thể cùng loài nhập cư vào quần thể (a) thì kích thước của quần thể này có thể thay đổi tăng nếu không có hiện tượng tử vong.

IV. Đúng. Điều kiện môi trường và sự cạnh tranh giữa các cá thể trong quần thể là các yếu tố chính ảnh hưởng đến sự phân bố cá thể của quần thể.

Chọn C.

Bài toán xét đến sự di truyền của 1 tính trạng, F₁: 9 : 7 \( \Rightarrow \) Tính trạng di truyền theo quy luật tương tác bổ sung. Quy ước: A-B-: thân cao; A-bb + aaB- + aabb: thân thấp.

- F₁ có 16 tổ hợp kiểu hình Þ P đều dị hợp 2 cặp gen Þ P: AaBb.

- P tự thụ: AaBb × AaBb → F₁: 9A-B- : 3A-bb : 3aaB- : 1aabb.

Þ Cây cao ở F₁: \[\frac{{1{\rm{ }}}}{9}AABB:\frac{2}{9}AABb:\frac{2}{9}AaBB:\frac{4}{9}AaBb.\]

Þ Tỉ lệ giao tử được tạo ra từ cây thân cao F₁: \[\frac{4}{9}AB:\frac{2}{9}Ab:\frac{2}{9}aB:\frac{1}{9}ab.\]

Þ Khi cho giao phấn ngẫu nhiên các cây cao F₁ với nhau, tỉ lệ các cây thân cao thu được ở F₂ là:

\[\begin{array}{l}AB \times \left( {AB,{\rm{ }}Ab,{\rm{ }}aB,{\rm{ }}ab} \right) + Ab \times \left( {AB,{\rm{ }}aB} \right) + aB \times \left( {AB,{\rm{ }}Ab} \right) + ab \times AB\\ = \frac{4}{9} \times 1 + \frac{2}{9} \times \frac{6}{9} + \frac{2}{9} \times \frac{6}{9} + \frac{1}{9} \times \frac{4}{9} = 79,01\% .\end{array}\]

Đáp án: 79,01%.

Nhân hóa: thác gầm thét, cọp trêu người. Chọn D.

Những câu thơ trong đoạn thơ cho biết tác giả nhấn mạnh chặng đường hành quân nhọc nhằn, gian khổ của các chiến sĩ Tây Tiến là các câu 3, 5, 6, 7. Điều này được thể hiện thông qua các từ ngữ mà tác giả Quang Dũng sử dụng trong từng câu. Cụ thể:

+ Câu 3: sương lấp, đoàn quân mỏi

+ Câu 5: dốc lên khúc khuỷu, dốc thăm thẳm

+ Câu 6: heo hút, cồn mây

+ Câu 7: ngàn thước lên cao, ngàn thước xuống

→ Chọn A.

Câu 13, 14 nhắc đến những kỉ niệm ngọt ngào của các chiến sĩ Tây Tiến với con người miền Tây: Nhớ ôi Tây Tiến cơm lên khói/ Mai Châu mùa em thơm nếp xôi. Chọn C.

Đoạn trích đã thể hiện nỗi nhớ của các chiến sĩ Tây Tiến hướng về con người và thiên nhiên miền Tây. Chọn C.

“dãi dầu” có nghĩa là trải qua nhiều mưa nắng, vất vả, gian truân. Chọn A.

Theo tác giả đoạn trích, biểu hiện của “ý thức về cá nhân và sở hữu không phát triển cao” thể hiện ở: Của cải vẫn được quan niệm là của chung, giàu sang chỉ là tạm thời, tham lam giành giật cho nhiều cũng không giữ mãi mà hưởng được. Chọn B.

Phong cách ngôn ngữ của đoạn trích là phong cách ngôn ngữ chính luận vì tác giả đoạn trích đã trình bày quan điểm của mình về lĩnh vực văn hóa, tư tưởng mà cụ thể là tôn giáo Việt Nam. Chọn D.

Người Việt Nam có thể coi là ít tinh thần tôn giáo. Điều này được lí giải bằng việc họ coi trọng hiện thế trần tục hơn thế giới bên kia. Chọn B.

Đoạn trích bàn về văn hóa Việt Nam trên các phương diện: tôn giáo, ý thức về cá nhân và sở hữu,… Chọn D.