Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 29)
36 người thi tuần này 4.6 1.8 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 37)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2026 có đáp án (Đề số 2)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 36)
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 35)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 30
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 29
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 34)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 28
Danh sách câu hỏi:
Câu 1
Lời giải
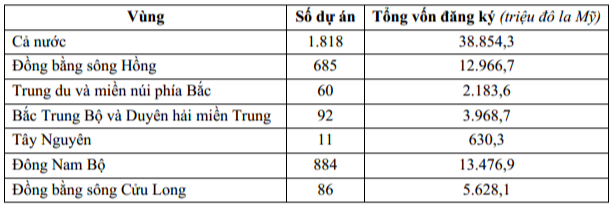
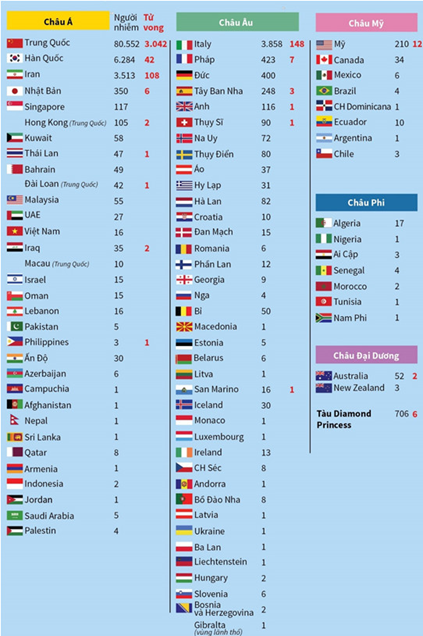
Dựa vào bảng số liệu ta có:
• Italy có 3858 ca nhiễm. • Hàn Quốc có 6284 ca nhiễm.
• Iran có 3513 ca nhiễm. • Mỹ có 210 ca nhiễm.
Như vậy, ngoài Trung Quốc thì Hàn Quốc có số ca nhiễm Covid-19 cao nhất.
Chọn B
Câu 2
Lời giải
Ta có \(s' = gt\).
Vận tốc tức thời tại thời điểm \(t = 5{\mkern 1mu} \,s\) là: \(v\left( 5 \right) = s'\left( 5 \right) = 5g = 49{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\). Chọn D.
Câu 3
Lời giải
Ta có: \[{\log _2}\left( {1 - x} \right) = 2 \Leftrightarrow 1 - x = 4 \Leftrightarrow x = - 3\]. Chọn B.
Câu 4
Lời giải
Ta có \(\left\{ {\begin{array}{*{20}{l}}{2{x^2} - 5xy + 2{y^2} = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\{2{x^2} - {y^2} = 7{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Khi đó \(\left( 1 \right) \Leftrightarrow \left( {2x - y} \right)\left( {x - 2y} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 2x}\\{x = 2y}\end{array}} \right.\)
• Với \(y = 2x\), ta có: \(\left( 2 \right) \Leftrightarrow 2{x^2} - {\left( {2x} \right)^2} = 7 \Leftrightarrow - 2{x^2} = 7{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)\)
• Với \(x = 2y\), ta có: \(\left( 2 \right) \Leftrightarrow 2.{\left( {2y} \right)^2} - {y^2} = 7 \Leftrightarrow 7{y^2} = 7 \Leftrightarrow y = \pm 1\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 1 \Rightarrow x = 2}\\{y = - 1 \Rightarrow x = - 2}\end{array}} \right..\)
Vậy hệ phương trình đã cho có hai nghiệm \(\left( {1\,;\,{\mkern 1mu} {\mkern 1mu} 2} \right)\) và \(\left( { - 1\,;\,{\mkern 1mu} {\mkern 1mu} - 2} \right).\) Chọn D.
Lời giải
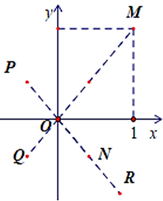
Gọi số phức \(z = a + bi{\mkern 1mu} {\mkern 1mu} \,\left( {a,b \in \mathbb{R}} \right)\) thì điểm \(N\left( {a\,;\,b} \right)\).
Khi đó số phức \(\frac{1}{z} = \frac{1}{{a + bi}} = \frac{{a - bi}}{{\left( {a + bi} \right)\left( {a - bi} \right)}} = \frac{{a - bi}}{{{a^2} + {b^2}}} = \frac{a}{{{a^2} + {b^2}}} - \frac{b}{{{a^2} + {b^2}}} \cdot i\)
Nên điểm biểu diễn số phức \(\frac{1}{z}\) có tọa độ \(\left( {\frac{a}{{{a^2} + {b^2}}}; - \frac{b}{{{a^2} + {b^2}}}} \right)\).
Vì điểm \(N\left( {a\,;\,b} \right)\) thuộc góc phần tư thứ (IV) tức là \(a > 0\,;\,\,b < 0\).
Suy ra \(\frac{a}{{{a^2} + {b^2}}} > 0;{\mkern 1mu} - \frac{b}{{{a^2} + {b^2}}} > 0\) nên điểm biểu diễn số phức \(\frac{1}{z}\) thuộc góc phần tư thứ (I). Từ hình vẽ chỉ có điểm \(M\) thỏa mãn. Chọn D.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(m > - \frac{4}{{1011}}\).
B. \(m \ge - \frac{4}{{3e + 2019}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. ví dụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. mục tiêu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. bảo đảm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. bồi dưỡng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. chia tách.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
A. Cột.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 107
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
A. sự khác nhau về cấu tạo mô giậu của lá.
B. có hiện tượng hô hấp sáng hay không.
C. sự khác nhau ở các phản ứng sáng.
D. sản phẩm cố định CO2 đầu tiên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 127
Một tế bào sinh tinh có kiểu gen \(\frac{{AB}}{{ab}}Dd\) đang giảm phân, trong đó cặp NST chứa hai cặp gen A, a và B, b không phân li ở giảm phân I, giảm phân II diễn ra bình thường; cặp D, d và các cặp NST khác phân li bình thường. Biết các gen không xảy ra hoán vị. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I. Kết thúc quá trình giảm phân tạo ra 4 giao tử đột biến.
II. Giao tử được tạo ra có thể có kiểu gen AB hoặc abDd.
III. Các giao tử được tạo ra có bộ NST là (n + 1) và (n - 1).
IV. Số loại giao tử tối đa được tạo ra là 2.
Một tế bào sinh tinh có kiểu gen \(\frac{{AB}}{{ab}}Dd\) đang giảm phân, trong đó cặp NST chứa hai cặp gen A, a và B, b không phân li ở giảm phân I, giảm phân II diễn ra bình thường; cặp D, d và các cặp NST khác phân li bình thường. Biết các gen không xảy ra hoán vị. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng?
I. Kết thúc quá trình giảm phân tạo ra 4 giao tử đột biến.
II. Giao tử được tạo ra có thể có kiểu gen AB hoặc abDd.
III. Các giao tử được tạo ra có bộ NST là (n + 1) và (n - 1).
IV. Số loại giao tử tối đa được tạo ra là 2.
A. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
(1) Doanh trại bừng lên hội đuốc hoa
(2) Kìa em xiêm áo tự bao giờ
(3) Khèn lên man điệu nàng e ấp
(4) Nhạc về Viên Chăn xây hồn thơ
(5) Người đi Châu Mộc chiều sương ấy
(6) Có thấy hồn lau nẻo bến bờ
(7) Có nhớ dáng người trên độc mộc
(8) Trôi dòng nước lũ hoa đong đưa.
(Tây Tiến – Quang Dũng)
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Bà lão cúi đầu nín lặng. Bà lão hiểu rồi. Lòng người mẹ nghèo khổ ấy còn hiểu ra biết bao nhiêu cơ sự, vừa ai oán vừa xót thương cho số kiếp đứa con mình. Chao ôi, người ta dựng vợ gả chồng cho con là lúc trong nhà ăn nên làm nổi, những mong sinh con đẻ cái mở mặt sau này. Còn mình thì... Trong kẽ mắt kèm nhèm của bà rỉ xuống hai dòng nước mắt... Biết rằng chúng nó có nuôi nổi nhau sống qua được cơn đói khát này không.
Bà lão khẽ thở dài ngửng lên, đăm đăm nhìn người đàn bà. Thị cúi mặt xuống, tay vân vê tà áo đã rách bợt. Bà lão nhìn thị và bà nghĩ: Người ta có gặp bước khó khăn, đói khổ này, người ta mới lấy đến con mình. Mà con mình mới có vợ được... Thôi thì bổn phận bà là mẹ, bà đã chẳng lo lắng được cho con... May ra mà qua khỏi được cái tao đoạn này thì thằng con bà cũng có vợ, nó yên bề nó, chẳng may ra ông giời bắt chết cũng phải chịu chứ biết thế nào mà lo cho hết được?
(Vợ nhặt – Kim Lân)
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
(1) Có hai hạt lúa nọ được giữ lại để làm hạt giống cho vụ sau vì cả hai đều là những hạt lúa tốt, đều to khỏe và chắc mẩy.
(2) Một hôm, người chủ định đem chúng gieo trên cánh đồng gần đó. Hạt thứ nhất nhủ thầm: “Dại gì ta phải theo ông chủ ra đồng. Ta không muốn cả thân mình phải nát tan trong đất. Tốt nhất ta hãy giữ lại tất cả chất dinh dưỡng trong lớp vỏ này và tìm một nơi lí tưởng để trú ngụ”. Thế là nó chọn một góc khuất trong kho lúa để lăn vào đó.
(3) Còn hạt lúa thứ hai thì ngày đêm mong được ông chủ mang gieo xuống đất. Nó thật sự sung sướng khi được bắt đầu một cuộc đời mới.
(4) Thời gian trôi qua, hạt lúa thứ nhất bị héo khô nơi góc nhà bởi vì nó chẳng nhận được nước và ánh sáng. Lúc này chất dinh dưỡng chẳng giúp ích được gì - nó chết dần chết mòn. Trong khi đó, hạt lúa thứ hai dù nát tan trong đất nhưng từ thân nó lại mọc lên cây lúa vàng óng, trĩu hạt. Nó lại mang đến cho đời những hạt lúa mới...
(5) Đừng bao giờ tự khép mình trong lớp vỏ chắc chắn để cố giữ sự nguyên vẹn vô nghĩa của bản thân mà hãy can đảm bước đi, âm thầm chịu nát tan để góp cho cánh đồng cuộc đời một cây lúa nhỏ - đó là sự chọn lựa của hạt giống thứ hai.
(Trích “Hạt giống tâm hồn”)
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Ngược lại với những kì vọng về sự hoàn hảo ở đứa trẻ, trong xã hội hiện đại, nhiều phụ huynh lo sợ con mình chịu áp lực, nên đã chủ trương để con thoải mái chơi là chính, không quan trọng việc học tập và rèn luyện để đạt thành tích tốt. Tôi cũng không đồng ý với quan điểm này. Bởi vì cuộc đời đứa trẻ rất dài, bố mẹ chỉ ở bên con cho đến tuổi trưởng thành. Khi bước vào đại học, các em sẽ phải va vấp xã hội. Lúc này bỏ mẹ không thể kiểm soát và giám sát. Trên con đường lập nghiệp, sẽ có rất nhiều áp lực, thậm chí là áp lực khủng khiếp. Để trẻ vượt qua những áp lực trên con đường đó thì chẳng cách nào tốt hơn là cha mẹ phải dạy trẻ “tự lái” ngay từ khi còn nhỏ.
Bản chất của áp lực là dương, nên cuộc sống luôn phải có một số áp lực. Một đứa trẻ không vượt qua nổi áp lực, sau này lớn lên, tôi tin đứa trẻ đó sẽ rất khó thành công trong cuộc sống. Nhưng có áp lực chịu được, có áp lực độc hại. Với một đứa trẻ, để dạy chúng “tự lái”, cha mẹ nên biết tạo áp lực vừa phải, đủ giúp chúng kiểm soát tốt bản thân và để cha mẹ hiểu tâm sinh lí, khả năng của con nhằm đồng hành với chúng.
(Áp lực thành tích - Trần Văn Phúc, Vnexpress, Thử bay. 18/12/2021)
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào thông tin dưới đây để trả lời các câu từ 109 đến 110:
-Bảo vệ biên giới Tây Nam: Do có âm mưu từ trước, ngay sau thắng lợi của cuộc kháng chiến chống Mỹ, cứu nước, tập đoàn “Khơme đỏ” ở Campuchia do Pôn Pốt cầm đầu đã mở những cuộc hành quân khiêu khích, xâm phạm nhiều vùng lãnh thổ nước ta từ Hà Tiên đến Tây Ninh. Đầu tháng 5-1975, chúng cho quân đổ bộ đánh chiếm đảo Phú Quốc ; sau đó đánh chiếm đảo Thổ Chu. Ngày 22-12-1978, chúng huy động 19 sư đoàn bộ binh cùng với nhiều đơn vị pháo binh, xe tăng tiến đánh Tây Ninh, mở đầu cuộc chiến tranh xâm lấn biên giới Tây Nam nước ta Thực hiện quyền tự vệ chính đáng, quân ta tổ chức cuộc phản công tiêu diệt và quét sạch quân xâm lược ra khỏi nước ta Theo yêu cầu của Mặt trận đoàn kết dân tộc cứu nước Campuchia, quân đội Việt Nam cùng với lực lượng cách mạng Campuchia tiến công, xoá bỏ chế độ diệt chủng Pôn Pốt. Ngày 7-1-1979, Thủ đô Phnôm Pênh được giải phóng.
-Bảo vệ biên giới phía Bắc: Hành động thù địch chống Việt Nam của tập đoàn Pôn Pốt được một số nhà lãnh đạo Trung Quốc lúc đó đồng tình ủng hộ. Họ còn có những hành động làm tổn hại đến tình hữu nghị của nhân dân hai nước như: cho quân khiêu khích dọc biên giới, dựng lên sự kiện “nạn kiều”, cắt viện trợ, rút chuyên gia Nghiêm trọng hơn, sáng 17- 2-1979, quân đội Trung Quốc huy động 32 sư đoàn mở cuộc tiến công dọc biên giới nước ta từ Móng Cái (Quảng Ninh) đến Phong Thổ (Lai Châu). Để bảo vệ lãnh thổ Tổ quốc, quân dân ta, trực tiếp là quân dân sáu tỉnh biên giới phía Bắc, đã đứng lên chiến đấu. Đến ngày 18-3-1979, quân Trung Quốc rút khỏi nước ta
(Nguồn: SGK Lịch sử 12, trang 206-207)
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

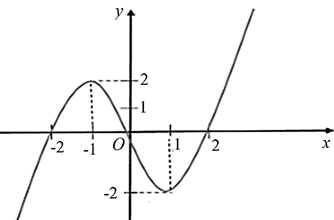
![Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Giá trị của \[m\] để phương trình \[f\left( {\sin x} \right) = m\] có đúng hai nghiệm trên đoạn \[\left[ {0\,;\,\,\pi } \right]\] và \[m \in \left( {a\,;\,\,b} \right]\] thì \(a + b\) bằng Đáp án: ………. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/08/blobid11-1722739728.png)