Đề kiểm tra Học kì 2 Toán 12 có đáp án (Mới nhất) - Đề 8
24 người thi tuần này 4.6 13.5 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Câu 1
A. (-1; 2; -1);
B. (1; -2; 1);
C. (3; 4; -3);
Lời giải
Đáp án đúng là: A
Ta có:
Vậy suy ra tọa độ của vectơ là (-1; 2; -1).
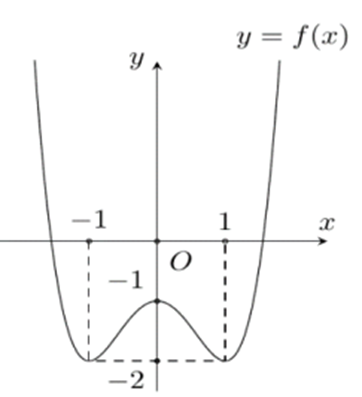
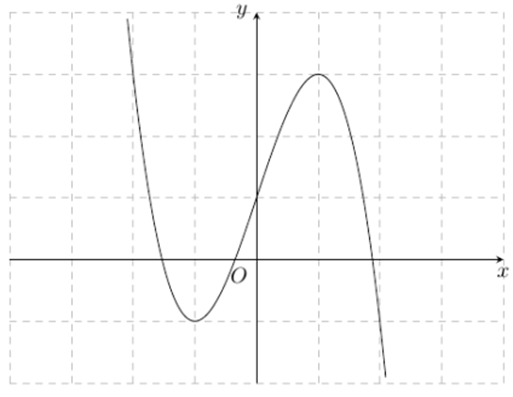
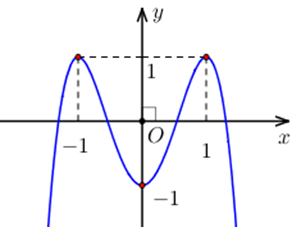
Câu 2
A. 3;
B. 1;
C. 2;
Lời giải
Đáp án đúng là: C
Ta nhận thấy rằng với y = f (x) = a (a > 0) cho hai nghiệm phân biệt.
Vậy suy ra số nghiệm của phương trình là 2 (do ).
Lời giải
Đáp án đúng là: C
Phương trình tham số của đường thẳng d đi qua điểm M (1; −1; 3) và có một vectơ chỉ phương là
Lời giải
Đáp án đúng là: D
Þ f '(x) = x3 - 20x = x(x2 - 20) = 0
Xét BBT của đồ thì hàm số trên [-2; 5]
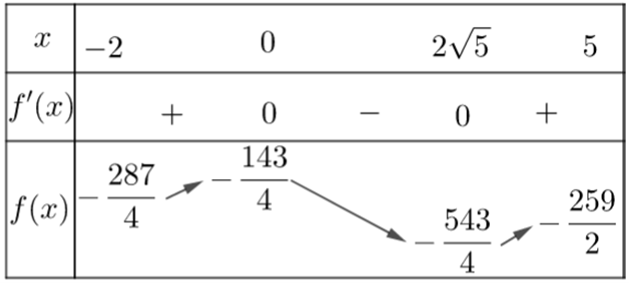
Dựa vào BBT, GTLN của hàm số f (x) trên [-2; 5] là
Câu 5
A. -2i;
B. 3;
C. -2;
Lời giải
Đáp án đúng là: B
Ta có z1.z2 = (2 - i)(1 + 2i)
= 2 + 4i - i - 2i2
= 2 + 4i - i + 2 = 4 + 3i
Khi đó phần ảo của số phức z1.z2 bằng 3.
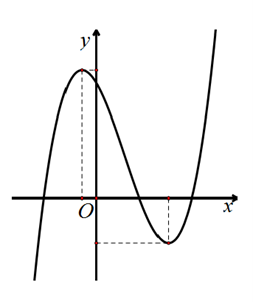
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 0;
B. -1;
C. 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. (0; 3);
B. (-1; 1);
C. (1; +);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. x = 2;
B. x = -2;
C. x = -1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. I(-3; -1; 2);
B. I(1; 2; 3);
C. I(3; 1; -2);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. I(1; -1; 4);
B. I(1; -1; 2);
C. I(4; -4; 16);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. 1;
B. 2;
C. 3;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. (-¥; +¥);
B. (1; +¥);
C. (0; 1);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. A(1; -2; -3);
B. A(-1; -2; 3);
C. A(-1; 2; 3);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. (-2; 5);
B. (2; 5);
C. (-2; 5);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. I = 3;
B. I = 9;
C. I = 27;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. F (x) = x2 + x - ln |x - 2| + 1;
B. F (x) = x2 + x - 2ln |x - 2| + 1;
C. F (x) = x2 + x - 2ln (2 - x) + 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. y' > 0, "x ¹ 1;
B. y' < 0, "x Î ℝ;
C. y' > 0, "x Î ℝ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. x = 1;
B. x = 4;
C. x = 2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. y = -x3 + 3x + 1;
B. y = x3 - 3x + 1;
C. y = x4 + 2x2 + 1;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. N(3; -1; -2);
B. N(-3; 1; 2);
C. N(-3; -1; -2);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. Đường thẳng x = 0;
B. Đường thẳng y = -x;
C. Đường thẳng y = x;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. 50 - 2a;
B. -30 + 2a;
C. 50 - a;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
A. min P = 8;
B. min P = 2;
C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. 0 £ m < 3;
B. -3 £ m < 0;
C. m < -3;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
A. (1; +¥);
B.
C.
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
A. 2;
B. 15;
C. 16;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
A. 3;
B. 1;
C. -3;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
A. a > 0, b < 0, c > 0, d > 0;
B. a > 0, b < 0, c > 0, d < 0;
C. a < 0, b < 0, c < 0, d > 0;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
A. 12;
B. 33;
C. 29;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
A. a chia hết cho 3;
B. 1 < a < 6;
C. a là số chính phương;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
A. 4;
B. 8;
C. 6;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.