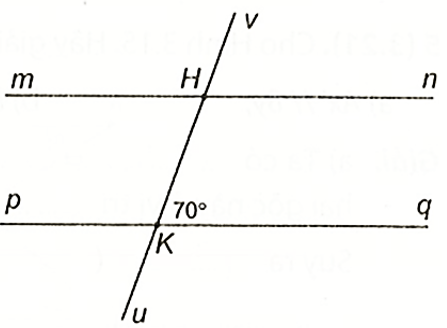
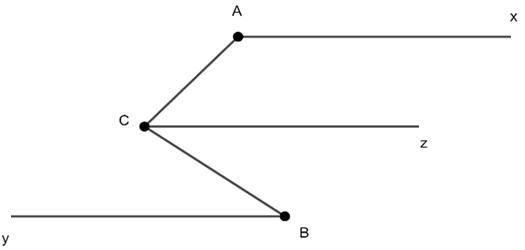
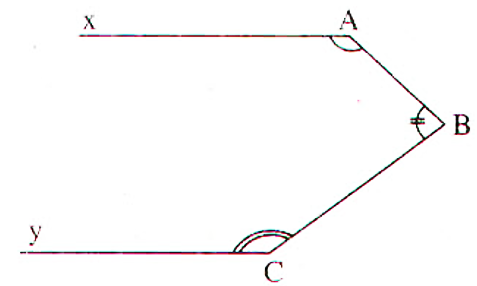
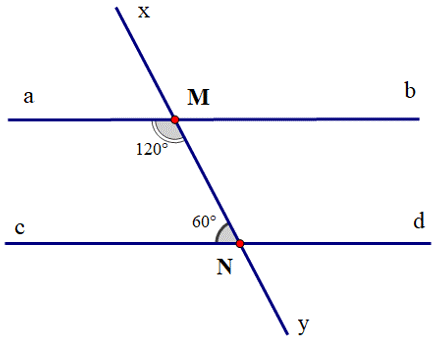
10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 15

Lời giải:

\(\overline {abc} \) = 11(a + b + c)

a.100 + b.10 + c

a.11 + b.11 + c.11

Suy ra a = 1 (vì b và c là số lớn nhất)

Vì b không phải số âm và không thể có 2 chữ số nên c = 8.

Ta có 89 = b + 10.c

Suy ra b = 89 − 10.c = 89 – 80 = 9.

Vậy số \(\overline {abc} \) thỏa mãn là 198.

Lời giải:

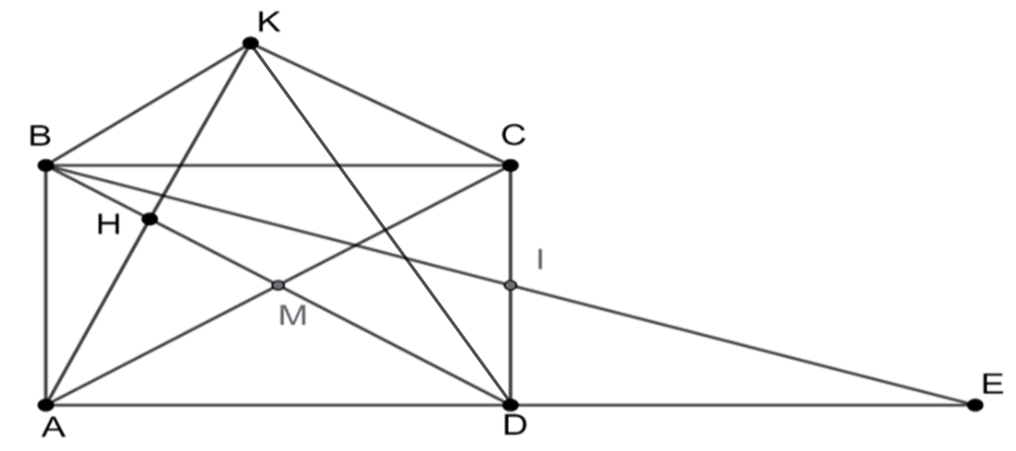
a) Xét tứ giác ABCD có M là trung điểm chung của AC và BD

Suy ra ABCD là hình bình hành.

Hình bình hành ABCD có \(\widehat {BAD}\)= 90° nên ABCD là hình chữ nhật.

b) Vì ABCD là hình chữ nhật nên AD // BC và AD = BC.

Mà D ∈ AE nên ED // BC; AD = BC.

Theo đề bài, DA = DE suy ra BC = ED.

Xét tứ giác EDBC có ED // BC; ED = BC.

Do đó EDBC là hình bình hành.

Suy ra EB cắt DC tại trung điểm của mỗi đường

Mà I là trung điểm của DC nên I là trung điểm của EB

Vậy IE = IB.

c) Xét ΔACK có H, M lần lượt là trung điểm của AK, AC

Suy ra HM là đường trung bình của ΔACK

Suy ra HM // CK nên CK // DB

Xét ΔDAK có DH vừa là đường cao vừa là đường trung tuyến.

Suy ra ΔDAK cân tại D nên DA = DK

Mà DA = BC (ABCD là hình chữ nhật) nên DK = BC

Xét tứ giác BKCD có CK // BD nên BKCD là hình thang.

Hình thang BKCD có CB = DK nên BKCD là hình thang cân

Lời giải:

Ta có: B = 1.2 + 2.3 + 3.4 + …..+ 31.32 + 32.33.

3B = 1.2.3 + 2.3.3 + 3.4.3 + …..+ 31.32.3 + 32.33.3

= 1.2.3 + 2.3.(4 – 1) +…….+ 31.32.(33 – 30) + 32. 33.(34 – 31)

= 1.2.3 + 2.3.4 – 2.3.1 +……+ 31.32.33 – 31.32.30 + 32.33.34 – 32.33.31

= 32.33.24

Suy ra B = \(\frac{{32.33.34}}{3} = 32.11.34\).

Mà 34 ⋮ 34 nên B = 32.11.34 ⋮ 34.

Lời giải:

• Từ 1 đến 2024 có 404 số chia hết cho 5 suy ra 2024! chia hết cho 5⁴⁰⁴

Nhận thấy n < 5⁵ với mọi n ∈ ℕ, n ≤ 2024

Suy ra \(\frac{{2024!}}{n}\) chia hết cho \({5^{404 - 5}}\)= 5³⁰⁹ với mọi n ∈ ℕ, n ≤ 2024

Nên \(\frac{{2024!}}{n}\) chia hết cho 25 với mọi n ∈ ℕ, n ≤ 2024

Do đó E ⋮ 25.         (1)

• Từ 1 đến 2024 có 674 số chia hết cho 3 suy ra 2024! chia hết cho 3⁶⁷⁴

Nhận thấy n < 3⁷ với mọi n ∈ ℕ, n ≤ 2024

Suy ra \(\frac{{2024!}}{n}\) chia hết cho 3^{674 – 7} = 3⁶⁶⁷ với mọi n ∈ ℕ, n ≤ 2024

Nên \(\frac{{2024!}}{n}\) chia hết cho 3⁴ = 81 với mọi n ∈ ℕ, n ≤ 2024

Suy ra E ⋮ 81 (2)

Từ (1) và (2) suy ra ƯCLN(25, 81) =1 nên E chia hết cho 25.81 = 2025.

Lời giải:

Số cần tìm có dạng \(\overline {abc} \).

a có 5 cách chọn

b có 6 cách chọn

c có 3 cách chọn

Vậy số lượng số cần tìm là :

5 × 6 × 3 = 90 (số)

Đáp số: 90 số

Lời giải:

Dãy số đã cho là dãy số cách đều 2 đơn vị

Số hạng thứ 99 trong dãy trên là

2 + (99 – 1) × 2 = 198

Vậy chữ số thứ 99 của dãy số 2, 4, 6, 8,…….., 100 là 198.

Lời giải:

Ta thấy MA + MB = AB.

Mà MA = 2 MB nên MB + 2MB = AB hay 3MB = AB.

Ta có AB = 6 cm nên 3MB = 6.

Suy ra MB = 6 : 3 = 2 (cm).

Lời giải:

Khi đem mỗi phân số đã cho trừ đi phân số a/b thì được 2 phân số mới có hiệu ko thay đổi và bằng \(\frac{7}{9}\)−\(\frac{5}{{11}}\)= \(\frac{{32}}{{99}}\).

Phân số bé mới là \(\frac{{32}}{{99}}\): (5 − 1) × 1 = \(\frac{8}{{99}}\).

Phân số \(\frac{a}{b}\) là \(\frac{5}{{11}}\)−\(\frac{8}{{99}}\)= \(\frac{{37}}{{99}}\).

Vậy phân số \(\frac{a}{b}\) cần tìm là \(\frac{{37}}{{99}}\).