ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Các loại dao động
36 người thi tuần này 4.6 2.3 K lượt thi 8 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
A.cưỡng bức.
B.tắt dần.
C.điều hoà.
D.duy trì.
Lời giải
Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động duy trì.
Đáp án cần chọn là: D
Câu 2
A.5 rad/s.
B.\[10\pi \] Hz.
C.5 Hz.
D.\[10\pi \] rad/s.
Lời giải
Hiện tượng cộng hưởng xảy ra khi:
\[\omega = {\omega _0} = 10\pi \Rightarrow f = \frac{{10\pi }}{{2\pi }} = 5\left( {Hz} \right)\]
Đáp án cần chọn là: C
Câu 3
A.Biên độ dao động cưỡng bức tăng rồi giảm
B.A1 = A2
C.A1 >A2
D.A1 < A2
Lời giải
Ta có:
+ Tần số dao động riêng của con lắc:
\[f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{{100}}{{0,1}}} = 5H{\rm{z}}\]
+ f0< f2
< f1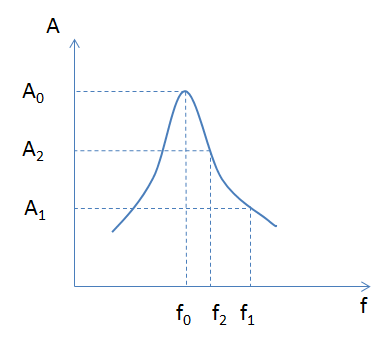
Từ đồ thị ta suy ra: A2>A1
Đáp án cần chọn là: D
Câu 4
A.Biên độ dao động cưỡng bức của một hệ cơ học khi xảy ra hiện tượng cộng hưởng không phụ thuộc vào lực cản của môi trường.
B.Tần số dao động cưỡng bức của một hệ cơ học bằng tần số của ngoại lực điều hòa tác dụng lên hệ ấy.
C.Hiện tượng cộng hưởng xảy ra khi tần số của ngoại lực điều hòa bằng tần số dao động riêng của hệ.
D.Tần số dao động tự do của một hệ cơ học là tần số dao động riêng của hệ ấy.
Lời giải
A - sai vì: Biên độ dao động cưỡng bức của hệ cơ học khi xảy ra hiện tượng cộng hưởng có phụ thuộc vào lực cản của môi trường
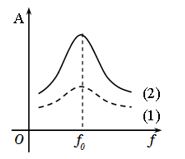
Đáp án cần chọn là: A
Lời giải
Ta có: \[\frac{{A - {A_3}}}{A} = 10{\rm{\% }} = 0,1 \to \frac{{{A_3}}}{A} = 0,9\]
Mặt khác, ta có: \[{\rm{W}} = \frac{1}{2}k{A^2}\]
\[ \to \frac{{{{\rm{W}}_3}}}{{\rm{W}}} = \frac{{A_3^2}}{{{A^2}}} = {0,9^2} = 0,81 = 81{\rm{\% }}\]
=>Phần trăm cơ năng còn lại sau khoảng thời gian đó là 81%
Đáp án cần chọn là: B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.8%.
B.10%.
C.4%.
D.7%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.