Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 50)
30 người thi tuần này 4.6 113.5 K lượt thi 48 câu hỏi 60 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \(\frac{8}{{89}}.\)
B. \(\frac{{81}}{{89}}.\)
C. \(\frac{{36}}{{89}}.\)
D. \(\frac{{53}}{{89}}.\)
Lời giải
Đáp án đúng là: A
Số tự nhiên có 2 chữ số là: \(C_9^1.C_{10}^1 = 90\) (số).
\(\Omega :\) “Chọn ngẫu nhiên 2 số từ tập hợp S” ⇒ \({n_\Omega } = C_{90}^2\)
A: “Chọn được 2 số có chữ số hàng đơn vị giống nhau”.
· TH1: Chữ số hàng đơn vị là 0 ⇒ Có 9 chữ số là: 10; 20; 30; 40; 50; 60; 70; 80; 90.
⇒ Số cách chọn 2 số là: \(C_9^2.\)
Tương tự với các số có chữ số hàng đơn vị là: 1; 2; 3; 4; 5; 6; 7; 8; 9.
⇒ Có tất cả 10 trường hợp giống nhau.
⇒ \({n_A} = 10.C_9^2\)
⇒ \({P_A} = \frac{{10.C_9^2}}{{C_{90}^2}} = \frac{8}{{89}}.\)
Lời giải
Vì S là tập hợp các số tự nhiên có hai chữ số nên tập S là tập hợp các số tự nhiên lớn hơn 9 và nhỏ hơn 100.
Do đó: S = {x | x là số tự nhiên và 9 < x < 100}.
Nhận thấy: 15; 99 là phần tử của S, 7; 106 không là phần tử của S
Vậy 7 ∉ S; 15 ∈ S; 106 ∉ S; 99 ∈ S.
Câu 3
A. 0.
B. 3.
C. 1.
D. 2.
Lời giải
Đáp án đúng là: C
ĐK: x > 0.
Đặt \(t = {\log _3}x = {\log _2}\left( {1 + \sqrt x } \right)\) (vì \(1 + \sqrt x > 1\) ⇒ \(t = {\log _2}\left( {1 + \sqrt x } \right) > 0\))
⇔ \(\left\{ {\begin{array}{*{20}{c}}{x = {3^t}}\\{1 + \sqrt x = {2^t}}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{x = {3^t}}\\{x = {{\left( {{2^t} - 1} \right)}^2}}\end{array}} \right.\)
⇒ \({3^t} = {\left( {{2^t} - 1} \right)^2}\) ⇔ \({3^t} = {4^t} - {2.2^t} + 1\) ⇔ \({\left( {\frac{3}{4}} \right)^t} = 1 - 2.{\left( {\frac{1}{2}} \right)^t} + {\left( {\frac{1}{4}} \right)^t}\)
⇔ \({\left( {\frac{3}{4}} \right)^t} + 2.{\left( {\frac{1}{2}} \right)^t} - {\left( {\frac{1}{4}} \right)^t} = 1\)
Xét hàm số \(f\left( t \right) = {\left( {\frac{3}{4}} \right)^t} + 2.{\left( {\frac{1}{2}} \right)^t} - {\left( {\frac{1}{4}} \right)^t}\) trên (0; +∞) có:
\(f'\left( t \right) = {\left( {\frac{3}{4}} \right)^t}\ln \frac{3}{4} + 2{\left( {\frac{1}{2}} \right)^t}\ln \frac{1}{2} - {\left( {\frac{1}{4}} \right)^t}\ln \frac{1}{4}\)
\( = {\left( {\frac{3}{4}} \right)^t}\ln \frac{3}{4} + 2{\left( {\frac{1}{2}} \right)^t}\ln \frac{1}{2} + 2.{\left( {\frac{1}{4}} \right)^t}\ln \frac{1}{2}\)
Mà \(\ln \frac{3}{4} < 0,\,\,\ln \frac{1}{2} < 0\) nên \(f'\left( t \right) < 0,\) ∀t > 0.
Do đó hàm số f(t) nghịch biến trên (0; +∞).
Dễ thấy f(2) = 1 nên phương trình f(t) = 1 có nghiệm duy nhất t = 2.
Suy ra \({\log _3}x = 2\) ⇔ x = 9.
Vậy phương trình có nghiệm duy nhất x = 9.
Lời giải
Đặt \({\log _2}x = 6t\) ⇒ x = 26t.
Thay vào phương trình ta có:
\(3{\log _3}\left( {1 + {2^{3t}} + {2^{2t}}} \right) = 2{\log _2}\left( {{2^{3t}}} \right) = 6t\)
⇔ \({\log _3}\left( {1 + {2^{3t}} + {2^{2t}}} \right) = 2t\)
⇔ \(1 + {2^{3t}} + {2^{2t}} = {3^{2t}}\)
⇔ \({\left( {\frac{1}{9}} \right)^t} + {\left( {\frac{8}{9}} \right)^t} + {\left( {\frac{4}{9}} \right)^t} = 1\) (chia cả 2 vế cho 32t)
Xét hàm số \(f\left( t \right) = {\left( {\frac{1}{9}} \right)^t} + {\left( {\frac{8}{9}} \right)^t} + {\left( {\frac{4}{9}} \right)^t} - 1\).
Ta thấy f(2) = 0.
Vì f(t) là hàm nghịch biến nên phương trình f(t) = 0 có 1 nghiệm duy nhất.
Suy ra t = 2 là nghiệm duy nhất.
Ta có: t = 2 ⇔ \({\log _2}x = 6.2 = 12\)
⇒ \(x = {2^{12}} = 4096\)
Vậy phương trình có nghiệm duy nhất x = 4096.
Lời giải
Đồ thị hàm số đi qua A và B nên \(\left\{ {\begin{array}{*{20}{c}}{a + b + c + d = - 7}\\{8a + 4b + 2c + d = - 8}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{d = - 7 - a - b - c}\\{7a + 3b + c = - 1\,\,\,\left( 1 \right)}\end{array}} \right.\)
Ta có: \(y' = 3a{x^2} + 2bx + c = 0\) có 2 nghiệm x = 1 và x = 2 (hoành độ của A và B) nên
\(\left\{ {\begin{array}{*{20}{c}}{3a + 2b + c = 0\,\,\left( 2 \right)}\\{12a + 4b + c = 0\,\,\left( 3 \right)}\end{array}} \right.\)
Từ (1), (2) và (3) ta có a = 2; b = −9; c = 12 ⇒ d = −12
Khi đó y(−1) = −a + b – c + d = −35.
Vậy y(−1) = −35.
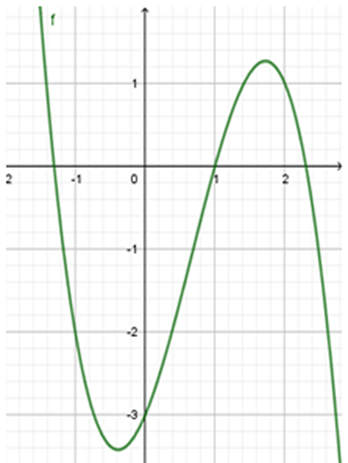
Câu 6
A. a < 0, b > 0, c > 0, d < 0.
B. a < 0, b < 0, c > 0, d < 0.
C. a > 0, b > 0, c > 0, d < 0.
D. a < 0, b > 0, c < 0, d < 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. z = 0.
B. x + y + z = 0.
C. y = 0.
D. x = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
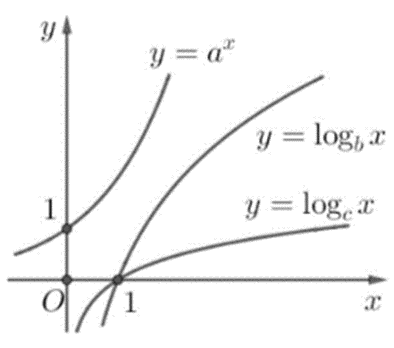
Câu 29
A. a < b < c.
B. c < b < a.
C. b < c < a.
D. b < a < c.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.