7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 59)
20 người thi tuần này 4.6 113.5 K lượt thi 42 câu hỏi 50 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \(30^\circ .\)
B. \(90^\circ .\)
C. \(60^\circ .\)
D. \(45^\circ .\)
Lời giải
Đáp án đúng là: D
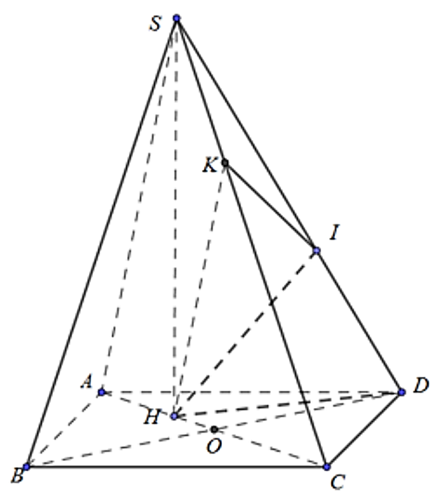
Gọi O là tâm hình thoi ABCD, H là trọng tâm tam giác ABD.
Tam giác ABD có: AB = AD (do ABCD là hình thoi), \(\widehat {BAD} = 60^\circ \)
⇒ ∆ABD đều ⇒ H là tâm đường tròn ngoại tiếp tam giác.
Hình chóp S.ABD có: SA = SB = SD = a ⇒ SH ⊥ (ABD).
Dựng HK // SA (K ∈ SC), HI ⊥ SD (I ∈ SD).
Mà HD ⊥ CD (do \[\widehat {HDC} = \widehat {HDO} + \widehat {ODC} = 30^\circ + 60^\circ = 90^\circ \])
⇒ CD ⊥ (SHD) ⇒ CD ⊥ HI.
⇒ HI ⊥ (SCD)
Ta có: \(\left( {\widehat {SA;\,\,\left( {SCD} \right)}} \right) = \left( {\widehat {HK;\,\,\left( {SCD} \right)}} \right) = \left( {\widehat {HK;\,\,KI}} \right) = \widehat {HKI}\)
HK // SA ⇒ \(\frac{{HK}}{{SA}} = \frac{{HC}}{{AC}} = \frac{2}{3}\) ⇒ \(HK = \frac{2}{3}a\)
Tứ diện S.ABD đều, có cạnh bằng a
⇒ \(\left\{ {\begin{array}{*{20}{c}}{HD = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}}\\{AH = \frac{2}{3}.OA = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}}\\{SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt 6 }}{3}}\end{array}} \right.\)
Xét tam giác SHD vuông tại H có:
HI ⊥ SD ⇒ \(\frac{1}{{H{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{D^2}}} = \frac{1}{{\frac{{2{a^2}}}{3}}} + \frac{1}{{\frac{{{a^2}}}{3}}} = \frac{9}{{2{a^2}}}\) ⇒ \(HI = \frac{{a\sqrt 2 }}{3}\)
Xét tam giác HIK vuông tại I có:
\(\sin \widehat {HKI} = \frac{{HI}}{{HK}} = \frac{{\frac{{a\sqrt 2 }}{3}}}{{\frac{{2a}}{3}}} = \frac{{\sqrt 2 }}{2}\) ⇒ \(\widehat {HKI} = 45^\circ \)
⇒ \(\left( {\widehat {SA;\,\,\left( {SCD} \right)}} \right) = 45^\circ .\)
Câu 2
A. \(\tan \alpha = \sqrt 5 .\)
B. \(\tan \alpha = \frac{{\sqrt 5 }}{5}.\)
C. \(\tan \alpha = \frac{{\sqrt 3 }}{2}.\)
D. \(\alpha = 45^\circ .\)
Lời giải
Đáp án đúng là: A
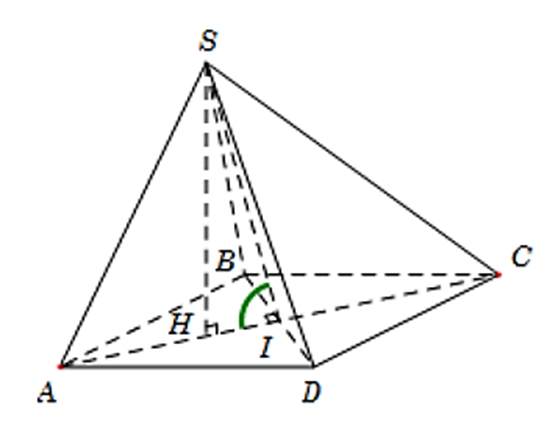
Từ giả thiết suy ra tam giác ABD đều cạnh a.
Gọi H là hình chiếu của S trên mặt phẳng (ABCD).
Do SA = SB = SD nên suy ra H là tâm của tam giác đều ABD.
⇒ \(\left\{ {\begin{array}{*{20}{c}}{AH = \frac{2}{3}.AI = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}}\\{HI = \frac{1}{3}.AI = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}}\\{SH = \sqrt {S{A^2} - A{H^2}} = \frac{{a\sqrt {15} }}{3}}\end{array}} \right.\)
Vì ABCD là hình thoi nên HI ⊥ BD. Tam giác SBD cân tại S nên SI ⊥ BD
⇒ \(\left( {\widehat {\left( {SBD} \right);\,\,\left( {ABCD} \right)}} \right) = \left( {\widehat {SI;\,\,AI}} \right) = \widehat {SIH}.\)
Trong tam giác vuông SHI, có \(\tan \widehat {SIH} = \frac{{SH}}{{HI}} = \sqrt 5 .\)
Câu 3
A. 560.
B. 4096.
C. 48.
D. 3360.
Lời giải
Đáp án đúng là: D
Mỗi cách bầu chọn một Ban chấp hành ba người gồm Bí thư, Phó Bí thư và Ủy viên là một chỉnh hợp chập 3 của 16 phần tử.
Do đó có \(A_{16}^3 = \frac{{16!}}{{13!}} = 3360\) (cách).
Lời giải
TXĐ: D = ℝ.
Ta có: \(y' = 3{x^2} - 3m = 0\) ⇔ x2 = m.
Để hàm số có hai điểm cực trị thì phương trình \(y' = 0\) có hai điểm cực trị ⇔ m > 0.
\(y' = 0\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{x = \sqrt m }\\{x = - \sqrt m }\end{array}} \right.\) ⇒ \[\left[ {\begin{array}{*{20}{c}}{y = - 2m\sqrt m + 1}\\{y = 2m\sqrt m + 1}\end{array}} \right.\]
⇒ \(\left[ {\begin{array}{*{20}{c}}{B\left( {\sqrt m ;\,\, - 2m\sqrt m + 1} \right)}\\{C\left( { - \sqrt m ;\,\,2m\sqrt m + 1} \right)}\end{array}} \right.\)
∆ABC cân tại A ⇒ AB = AC ⇔ AB2 = AC2
⇔ \({\left( {\sqrt m - 2} \right)^2} + {\left( { - 2m\sqrt m - 2} \right)^2} = {\left( { - \sqrt m - 2} \right)^2} + {\left( {2m\sqrt m - 2} \right)^2}\)
⇔ \(m - 4\sqrt m + 4 + 4{m^3} + 8m\sqrt m + 4 = m + 4\sqrt m + 4 + 4{m^3} - 8m\sqrt m + 4\)
⇔ \(8\sqrt m - 16m\sqrt m = 0\)
⇔ \(8\sqrt m \left( {1 - 2m} \right) = 0\)
⇔ \(m = \frac{1}{2}\) (do m > 0)
Vậy \(m = \frac{1}{2}.\)
Câu 5
A. 18.
B. -18.
C. \(\frac{{11}}{{23}}.\)
D. 2.
Lời giải
Đáp án đúng là: B
\(\sqrt {x + 2} = \sqrt {4 - x} \) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{x + 2 \ge 0}\\{4 - x \ge 0}\\{x + 2 = 4 - x}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 2}\\{x \le 4}\\{2x = 2}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{ - 2 \le x \le 4}\\{x = 1}\end{array}} \right.\) ⇔ x = 1.
Vậy S = {1}.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(\frac{{\sqrt 5 {a^3}}}{2}.\)
B. \(\frac{{\sqrt {35} {a^3}}}{2}.\)
C. \(\frac{{\sqrt {35} {a^3}}}{6}.\)
D. \(\frac{{\sqrt 5 {a^3}}}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. -2a2.
B. a2.
C. 2a2.
D. \( - \frac{{{a^2}}}{{\sqrt 2 }}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. a.
B. 0.
C. a2.
D. 2a2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. Một tam giác.
B. Một tứ giác.
C. Một ngũ giác.
D. Một lục giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. \(\frac{{\pi {a^3}}}{3}.\)
B. \(\frac{{\pi {a^3}}}{4}.\)
C. \(\frac{{\pi {a^3}\sqrt 3 }}{2}.\)
D. \(\frac{{\pi {a^3}\sqrt 3 }}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. 0,0494.
B. 0,0981.
C. 0,0170.
D. 0,0332.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. 0,001.
B. 0,002.
C. 0,003.
D. 0,004.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.