7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 71)
27 người thi tuần này 4.6 113.5 K lượt thi 41 câu hỏi 50 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
- Đề số 86
- Đề số 87
- Đề số 88
- Đề số 89
- Đề số 90
- Đề số 91
- Đề số 92
- Đề số 93
- Đề số 94
- Đề số 95
- Đề số 96
- Đề số 97
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \(\frac{{\sqrt 5 }}{{10}}\)
B. \(\frac{{3\sqrt {10} }}{{20}}\)
C. \(\frac{{\sqrt {10} }}{{20}}\)
D. \(\frac{{3\sqrt 5 }}{{10}}\).
Lời giải
Đáp án đúng là: B
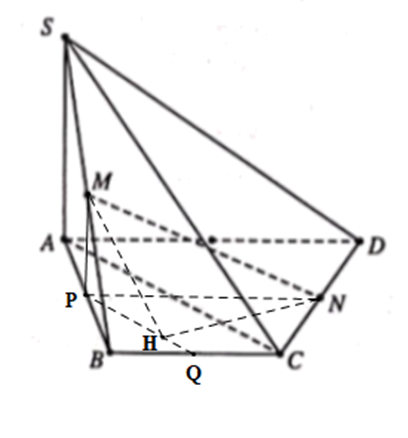
Diện tích hình thang cân ABCD là \({{\rm{S}}_{{\rm{ABCD}}}} = \frac{{3{{\rm{a}}^2}\sqrt 3 }}{4}\)
Mà \({V_{S.ABC{\rm{D}}}} = \frac{{{a^3}\sqrt 3 }}{4} \Rightarrow SA = a\)
Gọi P, Q lần lượt là trung điểm của AB, BC
Suy ra PQ là đường trung bình của tam giác ABC
Do đó PQ // AC \( \Rightarrow ({\rm{SAC}})\,{\rm{//}}\,({\rm{MPQ}}){\rm{ }}\)
Do đó: \(\widehat {\left( {{\rm{MN;}}\left( {SAC} \right)} \right)} = \widehat {\left( {MN;({\rm{MPQ}})} \right)} = (\widehat {{\rm{MN}};{\rm{NH}}}) = \widehat {{\rm{MNH}}}\) với H là hình chiếu của N trên PQ
Xét tam giác SAB có P, M lần lượt là trung điểm của AB, BS
Suy ra PM là đường trung bình
Do đó PM // SA \( \Rightarrow {\rm{MP}} \bot ({\rm{ABCD}})\)
Suy ra tam giác MPN vuông tại P
Khi đó \({\rm{MN}} = \sqrt {{\rm{M}}{{\rm{P}}^2} + {\rm{N}}{{\rm{P}}^2}} = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{3{\rm{a}}}}{2}} \right)}^2}} = \frac{{a\sqrt {10} }}{2}\) (định lý Pytago)
Ta có \({\rm{NH}} \bot {\rm{PQ}}\)
\( \Rightarrow {\rm{NH}} = \frac{3}{2}\;{\rm{d}}(\;{\rm{N}};({\rm{PQ}})) = \frac{3}{2}\;{\rm{d}}(\;{\rm{B}};({\rm{PQ}})) = \frac{3}{4}\)
Tam giác NMH vuông tại H, có \(\sin \widehat {MNH} = \frac{{NH}}{{MN}} = \frac{3}{4}:\frac{{\sqrt {10} }}{2} = \frac{{3\sqrt {10} }}{{20}}\)
Vậy ta chọn đáp án B.
Câu 2
A. S = πa2
B. \(S = \frac{{3\pi {a^2}}}{4}\)
C. S = 3πa2
D. S = 12πa2.
Lời giải
Đáp án đúng là C
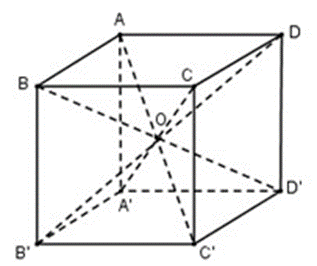
Vì ABCD là hình vuông nên AC = BD
Vì tam giác ABD vuông tại A nên \(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} \)
Suy ra \(AC = \sqrt {A{B^2} + A{{\rm{D}}^2}} \)
Vì tam giác AA’C’ vuông tại A’ nên \(AC' = \sqrt {AA{'^2} + A'C{'^2}} \)
Mà A’C’ = AC nên \(AC' = \sqrt {AA{'^2} + A{C^2}} \)
Hình lập phương ABCD.A’B’C’D’ có bán kính mặt cầu ngoại tiếp
\(R = \frac{1}{2}AC' = \frac{1}{2}\sqrt {A{C^2} + A'{A^2}} = \frac{1}{2}\sqrt {A{B^2} + A{D^2} + AA{'^2}} = \frac{1}{2}a\sqrt 3 \)
Diện tích mặt cầu đó là: \(S = 4\pi {R^2} = 4\pi .{\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\)
Vậy ta chọn đáp án C.
Câu 3
A. 10
B. 12
C. 6
D. 5
Lời giải
Đáp án đúng là D
Hàm số y = ln(x3 – 3m2x + 72m) xác định trên (0; +∞)
\( \Leftrightarrow {x^3} - 3{m^2}x + 72m > 0,\forall x > 0\)
Xét hàm số \(f(x) = {x^3} - 3{m^2}x + 72m\)
Ta có
\(\begin{array}{l}f'(x) = 3{x^2} - 3{m^2}\\f'(x) = 0 \Leftrightarrow 3{x^2} - 3{m^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = m}\\{x = - m}\end{array}} \right.\end{array}\)
Với m nguyên dương ta có bảng biến thiên:
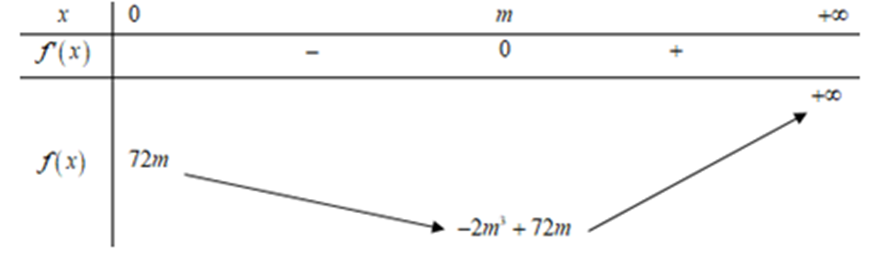
Do đó: \(f(x) > 0,\forall x > 0 \Leftrightarrow - 2{m^3} + 72m > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < - 6}\\{0 < m < 6}\end{array}} \right.\)
Vì \(m \in {\mathbb{Z}^ + } \Rightarrow m \in \{ 1;2;3;4;5\} \)
Suy ra có 5 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán
Vậy ta chọn đáp án D.
1122. log3(x cawnxx 3)
Câu 4
A. 0
B. 3
C. 1
D. 2.
Lời giải
Đáp án đúng là: C
Điều kiện: x > 0
Đặt \(t = {\rm{lo}}{{\rm{g}}_3}x = {\rm{lo}}{{\rm{g}}_2}\left( {1 + \sqrt x } \right)\) (vì \(1 + \sqrt x > 1 \Rightarrow t = {\rm{lo}}{{\rm{g}}_2}\left( {1 + \sqrt x } \right) > 0\))
\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = {3^t}}\\{1 + \sqrt x = {2^t}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = {3^t}}\\{x = {{\left( {{2^t} - 1} \right)}^2}}\end{array}} \right.} \right.\\ \Rightarrow {3^t} = {\left( {{2^t} - 1} \right)^2} \Leftrightarrow {3^t} = {4^t} - {2.2^t} + 1\end{array}\)
\(\begin{array}{l} \Leftrightarrow {\left( {\frac{3}{4}} \right)^t} = 1 - 2.{\left( {\frac{1}{2}} \right)^t} + {\left( {\frac{1}{4}} \right)^t}\\ \Leftrightarrow {\left( {\frac{3}{4}} \right)^t} + 2 \cdot {\left( {\frac{1}{2}} \right)^t} - {\left( {\frac{1}{4}} \right)^t} = 1\end{array}\)
Xét hàm số \(f\left( t \right) = {\left( {\frac{3}{4}} \right)^t} + 2 - {\left( {\frac{1}{4}} \right)^t}\) trên (0; +∞) có:
\(\begin{array}{l}f'\left( t \right) = {\left( {\frac{3}{4}} \right)^t}{\rm{ln}}\frac{3}{4} + 2{\left( {\frac{1}{2}} \right)^t}{\rm{ln}}\frac{1}{2} - {\left( {\frac{1}{4}} \right)^t}{\rm{ln}}\frac{1}{4}\\ = {\left( {\frac{3}{4}} \right)^t}{\rm{ln}}\frac{3}{4} + 2{\left( {\frac{1}{2}} \right)^t}{\rm{ln}}\frac{1}{2} + 2 \cdot {\left( {\frac{1}{4}} \right)^t}{\rm{ln}}\frac{1}{2}\end{array}\)
Mà \({\rm{ln}}\frac{3}{4} < 0,{\rm{ln}}\frac{1}{2} < 0\) nên f’(t) < 0; ∀ t > 0
Do đó hàm số f(t) nghịch biến trên (0; +∞)
Dễ thấy f(2) = 1 nên phương trình f(t) = 1 có nghiệm duy nhất t = 2
Suy ra \({\rm{lo}}{{\rm{g}}_3}x = 2 \Leftrightarrow x = 9\)
Vậy ta chọn đáp án C.
Câu 5
A. \({\log _2}\left( {\frac{{x + 2y}}{4}} \right) = {\log _2}x - {\log _2}y\)
B. \(\log 2\left( {x + 2y} \right) = 2 + \frac{1}{2}\left( {{{\log }_2}x + {{\log }_2}y} \right)\)
C. \({\log _2}\left( {x + 2y} \right) = {\log _2}x + {\log _2}y + 1\)
D. \(4{\log _2}\left( {x + 2y} \right) = {\log _2}x + {\log _2}y\).
Lời giải
Đáp án đúng là: B
Vì \({x^2} + 4{y^2} = 12xy\) nên \({(x + 2y)^2} = 16xy\) hay \({\log _2}{(x + 2y)^2} = {\log _2}16xy\)
Do đó: \(2{\log _2}(x + 2y) = 4 + {\log _2}x + {\log _2}y\)
Suy ra \(\log 2\left( {x + 2y} \right) = 2 + \frac{1}{2}\left( {{{\log }_2}x + {{\log }_2}y} \right)\)
Vậy ta chọn đáp án B.
Câu 6
A. \(\frac{4}{5}\)
B. \(\frac{5}{6}\)
C. \(\frac{6}{5}\)
D. \(\frac{5}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\sqrt 2 \pi {a^3}\)
B. \(\frac{{\sqrt 2 \pi {a^3}}}{3}\)
C. \(\frac{{\pi {a^3}}}{6}\)
D. \(\frac{{\pi {a^3}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(\frac{4}{3}\)
B. \(\frac{2}{3}\)
C. \(\frac{1}{{18}}\)
D. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. m ≥ 1
B. m ≥ 0
C. m ≠ 0
D. m > 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 1
B. 3
C. Vô số
D. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. D = R
B. D = (0; +∞)
C. D = (–∞;–1) ∪ (2; +∞)
D. D = R \ {–1; 2}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(\frac{1}{{11}}\)
B. \(\frac{1}{{22}}\)
C. \(\frac{5}{{18}}\)
D. \(\frac{{19}}{{66}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(\frac{{{a^3}}}{3}\)
B. \(\frac{{{a^3}}}{9}\)
C. \[{{\rm{a}}^3}\sqrt 2 \]
D. \(\frac{{{a^3}}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \(\frac{{4000\pi {a^3}}}{{81}}\)
B. \(\frac{{4000\pi {a^3}}}{{27}}\)
C. \(\frac{{40\pi {a^3}}}{9}\)
D. \(\frac{{400\pi {a^3}}}{{27}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \(\frac{{{a^3}\sqrt 5 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 5 }}{4}\)
C. \(\frac{{{a^3}\sqrt 5 }}{2}\)
D. \(\frac{{{a^3}\sqrt 5 }}{6}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \[{\rm{d}}\left( {AB,d} \right) = \frac{{R\sqrt 3 }}{2}\]
B. \[{\rm{d}}\left( {AB,d} \right) = R\]
C. \[{\rm{d}}\left( {AB,d} \right) = R\sqrt 3 \]
D. \[{\rm{d}}\left( {AB,d} \right) = \frac{R}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \(32\pi {a^3}\sqrt 6 \)
B. \(24\pi {a^3}\sqrt 6 \)
C. \(16\pi {a^3}\sqrt 6 \)
D. \(8\pi {a^3}\sqrt 6 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. \({S_{ABC}} = 3\sqrt 3 \)
B. \({S_{ABC}} = 6\sqrt 3 \)
C. \({S_{ABC}} = 9\sqrt 3 \)
D. \({S_{ABC}} = \frac{{3\sqrt 3 }}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. \[{\rm{R}}\backslash \left\{ { \pm \frac{5}{3}} \right\}\]
B. \(\left( {\frac{5}{3}; + \infty } \right)\)
C. \(\left( { - \frac{1}{2}; + \infty } \right)\backslash \left\{ {\frac{5}{3}} \right\}\)
D. \(\left( { - \frac{1}{2}; + \infty } \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \(\frac{a}{b} = a + b\) với a, b > 0.
B. a + b = ab với a, b > 0.
C. a + b = 2ab với a, b > 0.
D. 2(a + b) = ab với a, b > 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. \(\frac{2}{{25}}\)
B. \(\frac{1}{{12}}\)
C. \(\frac{3}{{25}}\)
D. \(\frac{5}{{48}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. \(m > \frac{1}{3}\)
B. m < –1
C. \(m > \frac{1}{3}\) hoặc m < –1
D. \( - 1 < m < \frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. (–2; –1)
B. (–2; 0)
C. (0; 1)
D. (–1; 0).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. \(\frac{{12}}{5}a\)
B. 2a
C. \(\frac{3}{2}a\)
D. \(\frac{9}{4}a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \(V = \frac{{\pi {a^2}h}}{9}\)
B. \(V = \frac{{\pi {a^2}h}}{3}\)
C. \(V = 3\pi {a^2}h\)
D. \(V = \pi {a^2}h\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. 1
B. 3
C. 2
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. y = x + 2
B. y = –x – 1
C. y = x + 3
D. y = –x + 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. \(\frac{1}{6}\)
B. \(\frac{3}{{20}}\)
C. \(\frac{2}{{15}}\)
D. \(\frac{1}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. 2
B. 4
C. 5
D. 6.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. 80 cm
B. 100 cm
C. \(100\sqrt 2 \) cm
D. 140 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. \(m = \frac{{ - 1}}{2}\)
B. m ∈ ∅
C. m = 0
D. \(m = \frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. m > 0
B. m ≥ 2
C. không tồn tại m
D. \(\left\{ \begin{array}{l}m > 0\\m \ne \ln 3\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
A. \(m \in \left( { - 1;\frac{3}{2}} \right)\)
B. \(m \in \left( {\frac{1}{2}; + \infty } \right)\)
C. \(m \in \left( {0; + \infty } \right)\)
D. \(m \in \left[ { - 1;\frac{3}{2}} \right]\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
A. 35
B. 90
C. 60
D. 45.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. x – 2y – 12 = 0
B. –x + 2y – 13 = 0
C. –x + 2y + 8 = 0
D. –x + 2y + 13 = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 41
A. \(\frac{{{a^3}\sqrt 3 }}{6}\)
B. \(\frac{{{a^3}\sqrt 3 }}{3}\)
C. \(\frac{{{a^3}\sqrt {15} }}{{10}}\)
D. \({a^3}\sqrt 3 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
