5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 46)

52 người thi tuần này 4.6 60.1 K lượt thi 52 câu hỏi 60 phút

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41
Đề số 42
Đề số 43
Đề số 44
Đề số 45
Đề số 46
Đề số 47
Đề số 48
Đề số 49
Đề số 50
Đề số 51
Đề số 52
Đề số 53
Đề số 54
Đề số 55
Đề số 56
Đề số 57
Đề số 58
Đề số 59
Đề số 60
Đề số 61
Đề số 62
Đề số 63
Đề số 64
Đề số 65
Đề số 66
Đề số 67
Đề số 68
Đề số 69
Đề số 70
Đề số 71
Đề số 72
Đề số 73
Đề số 74
Đề số 75
Đề số 76
Đề số 77
Đề số 78
Đề số 79
Đề số 80
Đề số 81
Đề số 82
Đề số 83
Đề số 84
Đề số 85

🔥 Đề thi HOT:

2867 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

62.5 K lượt thi 126 câu hỏi

2316 người thi tuần này

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

15.3 K lượt thi 35 câu hỏi

1379 người thi tuần này

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

14 K lượt thi 20 câu hỏi

1374 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

13.1 K lượt thi 20 câu hỏi

1337 người thi tuần này

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

13.4 K lượt thi 40 câu hỏi

1307 người thi tuần này

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

16 K lượt thi 35 câu hỏi

1287 người thi tuần này

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

20.5 K lượt thi 25 câu hỏi

1042 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

9.8 K lượt thi 15 câu hỏi

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

19317 lượt thi

8 đề

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

15177 lượt thi

8 đề

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

16437 lượt thi

7 đề

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

14828 lượt thi

7 đề

225 Bài tập Số phức ôn thi Đại học có lời giải

11231 lượt thi

8 đề

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

23358 lượt thi

10 đề

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

20815 lượt thi

9 đề

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

13053 lượt thi

8 đề

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

7556 lượt thi

7 đề

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

6233 lượt thi

3 đề

Danh sách câu hỏi:

Câu 1

Giải phương trình \({\sin ^2}\frac{x}{2} - 2co{s^2}\frac{x}{4} = \frac{3}{4}\).

Xem đáp án

Lời giải

Ta có:

\({\sin ^2}\frac{x}{2} - 2co{s^2}\frac{x}{4} = \frac{3}{4}\)

\[ \Leftrightarrow \left( {1 - co{s^2}\frac{x}{2}} \right) - \left( {cos\frac{x}{2} + 1} \right) = \frac{3}{4}\]

\[ \Leftrightarrow 1 - co{s^2}\frac{x}{2} - cos\frac{x}{2} - 1 - \frac{3}{4} = 0\]

\[ \Leftrightarrow co{s^2}\frac{x}{2} + cos\frac{x}{2} + \frac{3}{4} = 0\]

\[ \Leftrightarrow \left( {co{s^2}\frac{x}{2} + 2.cos\frac{x}{2}.\frac{1}{2} + \frac{1}{4}} \right) + \frac{1}{2} = 0\]

\[ \Leftrightarrow {\left( {cos\frac{x}{2} + \frac{1}{2}} \right)^2} + \frac{1}{2} = 0\] (vô nghiệm).

Vậy phương trình đã cho vô nghiệm.

Câu 2

Tìm m để đường thẳng y = 2x – 1 và y = 3x + m cắt nhau tại một điểm nằm trên trục hoành.

Xem đáp án

Lời giải

Gọi (d): y = 2x – 1 và (d’): y = 3x + m.

Trục Ox: y = 0.

Phương trình hoành độ giao điểm của (d) và Ox: \(2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}\).

Với \(x = \frac{1}{2}\), ta có: y = 0.

Suy ra giao điểm của (d) và trục hoành là \(I\left( {\frac{1}{2};0} \right)\).

Yêu cầu bài toán ⇔ Đường thẳng (d’) đi qua điểm \(I\left( {\frac{1}{2};0} \right)\).

Ta có I ∈ (d’). Suy ra \(0 = 3.\frac{1}{2} + m\).

\( \Leftrightarrow m = - \frac{3}{2}\).

Vậy \(m = - \frac{3}{2}\) thỏa mãn yêu cầu bài toán.

Câu 3

Từ các điểm A, B, C, D, E không thẳng hàng, ta có thể lập được bao nhiêu tam giác mà các đỉnh của tam giác được lấy từ 5 điểm A, B, C, D, E?

A. \(C_5^3 = 10\);

B. \(A_5^3 = 60\);

C. \({P_5} = 120\);

D. \({P_3} = 6\).

Lời giải

Đáp án đúng là: A

Cứ 3 điểm không thẳng hàng ta lập được 1 tam giác.

Vậy để lập được tam giác mà các đỉnh của tam giác được lấy từ 5 điểm A, B, C, D, E thì ta chọn 3 điểm trong 5 điểm, có \(C_5^3 = 10\).

Câu 4

Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. Gọi M là trung điểm của CD. Tìm giao điểm E của SD và mặt phẳng IJM.

Xem đáp án

Lời giải

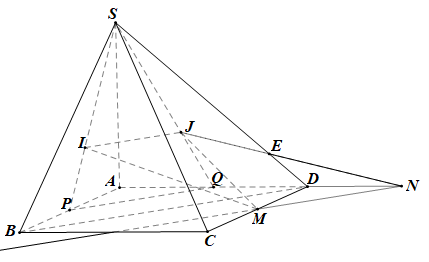
Media VietJack

Gọi P, Q lần lượt là trung điểm của AB, AD.

Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.

Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên \(\frac{{SI}}{{SP}} = \frac{2}{3} = \frac{{SJ}}{{SQ}}\).

Do đó IJ // PQ, suy ra IJ // BD

Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)

Þ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.

Đường thẳng này cắt AD tại N.

Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)

Trong mp(SAN), JN cắt SD tại E.

Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)

Khi đó E là giao điểm của SD và (IJM).

Câu 5

Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm tam giác ABA’ và M là điểm tùy ý trên đường thẳng B’C’. Đường thẳng MG cắt mặt phẳng (ABC) tại điểm N. Tỉ số \(\frac{{GM}}{{GN}}\) bằng

A. \(\frac{1}{2}\);

B. 2;

C. 3;

D. \(\frac{1}{3}\).

Lời giải

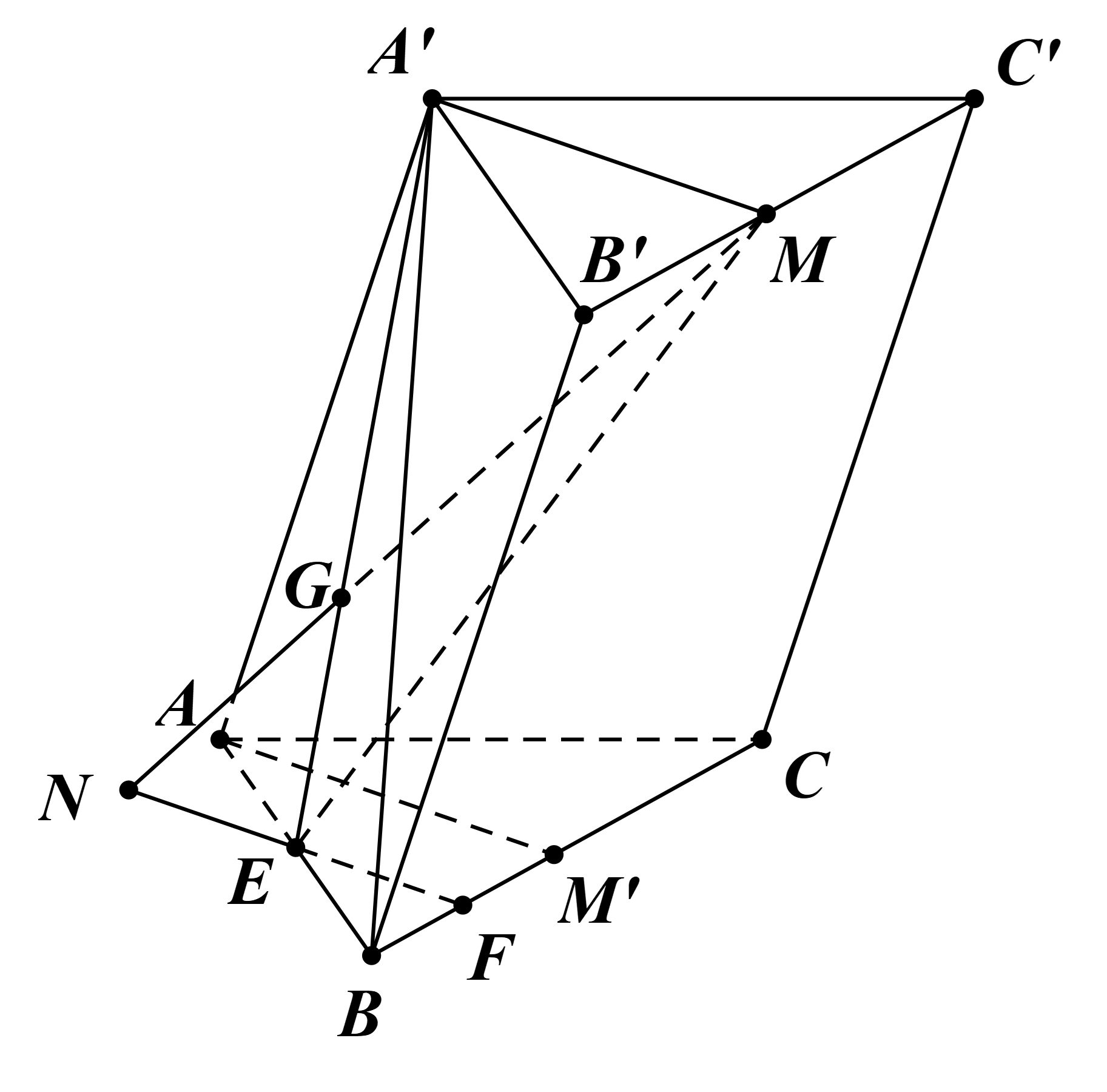
Media VietJack

Gọi E là giao điểm của A’G và AB.

Suy ra E ∈ (A’MG) ∩ (ABC).

Trong (AA’M): kẻ AM’ // A’M, M’ ∈ BC.

Trong (ABC): dựng EF // AM’, F ∈ BC.

Khi đó EF là giao tuyến của (A’MG) và (ABC).

Trong (A’MG): MG ∩ EF = I.

Khi đó I là giao điểm của MG và (ABC).

Vì vậy N ≡ I.

Trong (A’MG), ta có NE // A’M.

Áp dụng định lí Thales, ta được \(\frac{{GM}}{{GN}} = \frac{{GA'}}{{GE}} = 2\).

Vậy ta chọn phương án B.

Câu 6

Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại D và E.

a) Chứng minh CD vuông góc với AB, BE vuông góc với AC.

b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H.

a) Chứng minh tứ giác AEHF nội tiếp.

b) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF. Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu \(\widehat {BAC} = 60^\circ \), AH = 4 cm.

c) AH giao BC tại D. Chứng minh FH là tia phân giác của \(\widehat {DFE}\).

d) Chứng minh 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại một điểm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Hiệu 2 số là 66,8. Nếu dịch dấu phẩy của số bé sang trái một hàng thì hiệu mới là 117,83. Tìm số lớn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Rô-bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để Rô-bốt lấy được 100 ml nước từ chậu nước?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho biểu thức \[P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\].

a) Tìm x nguyên để P nhận giá trị nguyên.

b) Tìm x sao cho P > 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Cho 2 tập khác rỗng A = (m – 1; 4]; B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ⊂ B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho tam giác ABC. Tìm điểm M sao cho \(\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} = \vec 0\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Đơn giản biểu thức sau khi bỏ ngoặc:

a) –a – (b – a – c);

b) – (a – c) – (a – b + c);

c) b – (b + a – c);

d) –(a – b + c) – (a + b + c);

e) (a + b) – (a – b) + (a – c) – (a + c);

g) (a + b – c) + (a – b + c) – (b + c – a) – (a – b – c).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Đơn giản biểu thức sau khi bỏ dấu ngoặc:

a) (a + b – c) – (b – c + d);

b) –(a – b + c) + (a – b + d);

c) (a + b) – (–a + b – c);

d) –(a + b) + (a + b + c);

e) (a – b + c) – (a – b + c);

f) –(a – b – c) + (a – b – c).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh:

a) ∆ADB = ∆ADC.

b) AD là tia phân giác của \(\widehat {BAC}\) và \(\widehat B = \widehat C\).

c) AD vuông góc với BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho tam giác ABC có AB = AC. Gọi D là trung điểm của cạnh BC.

a) Chứng minh rằng ∆ABD = ∆ACD và AD là tia phân giác của \(\widehat {BAC}\).

b) Vẽ DM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho AN = AM. Chứng minh ∆ADM = ∆ADN và DN vuông góc AC.

c) Gọi K là trung điểm của đoạn thẳng CN. Trên tia đối của tia KD lấy điểm E sao cho KE = KD. Chứng minh M, E, N thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Số đối của 24 là gì?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Tìm x biết:

a) (x – 5).(x + 4) = 0;

b) x² – 7x = 0;

c) x² = –5x;

d) x³ = x;

e) (x – 5).(x – 4) = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho 3x² + 3y² = 10xy với y > x > 0. Tính giá trị của biểu thức \(K = \frac{{x + y}}{{x - y}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Giải phương trình 5sin²x + 3sinxcosx – 4cos²x = 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho các tập hợp A = {x ∈ ℝ | x ≤ a}; B = {x ∈ ℝ | x ≥ b}; C = [–5; 5]. Biết rằng A ∩ C; B ∩ C là các đoạn có độ dài lần lượt là 7 và 9. Tìm tập A ∩ B.

A. A ∩ B = [–4; 2];

B. A ∩ B = (–4; 2);

C. A ∩ B = [–4; +∞);

D. A ∩ B = (–∞; 2).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho \(A = \sqrt {{{2018}^2} + {{2018}^2}{{.2019}^2} + {{2019}^2}} \). Chứng minh A là một số tự nhiên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n³ – 4n² + 4n – 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.

A. \(\left[ \begin{array}{l}a < 3\\a \ge 4\end{array} \right.\);

B. a < 3;

C. a < 0;

D. a > 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Tìm x biết: x⁴ + 2x³ – 6x – 9 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Giải phương trình \(\cos \left( {2x + \frac{\pi }{4}} \right) = \frac{1}{2},\,\, - \pi < x < \pi \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Giải phương trình \(\cos \left( {2x - \frac{\pi }{4}} \right) = \frac{1}{2}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Giải phương trình cos2x – 3cosx + 2 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Khi chuyển hỗn số \(34\frac{6}{x}\) về dạng phân số thì ta được phân số tối giản A có tổng tử số và mẫu số là 461. Giá trị của x là bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Cho \(Q = \left( {\frac{1}{{x - 4}} - \frac{1}{{x + 4\sqrt x + 4}}} \right).\frac{{x + 2\sqrt x }}{{\sqrt x }}\).

a) Tìm điều kiện xác định của biểu thức Q.

b) Rút gọn Q.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Rút gọn biểu thức sau: \(B = \left( {\frac{1}{{x - 4}} - \frac{1}{{x - 4\sqrt x + 4}}} \right).\frac{{x + 2\sqrt x }}{{\sqrt x }}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Giải phương trình lượng giác: sin²2x + sin²4x = sin²6x.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Giải phương trình sau: \({\sin ^2}2x = \frac{1}{2}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

a) Cho biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\] với x ≥ 0. Tính giá trị của A khi x = 16.

b) Cho biểu thức \(B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\) với x ≥ 0; x ≠ 1. Rút gọn B.

c) Tìm các số hữu tỉ x để P = A.B có giá trị nguyên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Tìm x biết: \(\sqrt {16x} - 2\sqrt {36x} + 3\sqrt {9x} = 2\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:

a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \).

b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB} \).

c) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Cho tam giác ABC. Hãy tìm các điểm M thỏa các điều kiện:

a) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} \).

b) \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {AB} \).

c) \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {BA} \).

d) \(\left| {\overrightarrow {MA} - \overrightarrow {CA} } \right| = \left| {\overrightarrow {AC} - \overrightarrow {AB} } \right|\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Cho mười chữ số 0, 1, 2, 3, …, 9. Có bao nhiêu số tự nhiên lẻ gồm 6 chữ số khác nhau, nhỏ hơn 600000 được xây dựng từ 10 số trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Tìm tổng của số lẻ nhỏ nhất có ba chữ số khác nhau với số chẵn lớn nhất gồm 2 chữ số chẵn khác nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Tính tổng sau: 1 + 2 + 3 + … + 99.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Tìm nghiệm nguyên của phương trình: 7(x² + xy + y²) = 39(x + y).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Giải phương trình \(\frac{{m!\,\, - \left( {m - 1} \right)!}}{{\left( {m + 1} \right)!}} = \frac{1}{6}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Nếu \(C_n^{12} = C_n^8\) thì \(C_n^{17}\) bằng bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Phương trình \(\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi:

A. –1 < m < 0;

B. –3 < m < –1;

C. \(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\);

D. \(\left[ \begin{array}{l}m < - 2\\m > 0\end{array} \right.\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Giải phương trình: x³(x² – 7)² – 36x = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Tìm x, biết: \(\left( {x - \frac{2}{7}} \right)\left( {x + \frac{3}{4}} \right) = 0\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Tìm nghiệm x thuộc [0; 2π] của phương trình \(5\left( {\sin x + \frac{{\cos 3x + \sin 3x}}{{1 + 2\sin 2x}}} \right) = \cos 2x + 3\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Nghiệm của phương trình \[A_x^{10} + A_x^9 = 9A_x^8\] là:

A. x = 10;

B. x = 9;

C. x = 11;

D. x = 9 hoặc \(x = \frac{{91}}{9}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

a) A = cos⁴x – cos²x + sin²x;

b) B = sin⁴x – sin²x + cos²x.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Cho tam giác ABC, hai điểm M, N được xác định bởi \(3\overrightarrow {MA} + 4\overrightarrow {MB} = \vec 0\); \(\overrightarrow {NB} - 3\overrightarrow {NC} = \vec 0\). Chứng minh 3 điểm M, G, N thẳng hàng, với G là trọng tâm tam giác ABC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Cho các đa thức sau: A = x³ + 4x² + 3x – 7 và B = x + 4.

a) Tính A : B.

b) Tìm x ∈ ℤ sao cho A chia hết cho B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

4.6

12016 Đánh giá

50%

40%

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 46)

🔥 Đề thi HOT:

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

Danh sách câu hỏi:

Giải phương trình \({\sin ^2}\frac{x}{2} - 2co{s^2}\frac{x}{4} = \frac{3}{4}\).

Tìm m để đường thẳng y = 2x – 1 và y = 3x + m cắt nhau tại một điểm nằm trên trục hoành.

Từ các điểm A, B, C, D, E không thẳng hàng, ta có thể lập được bao nhiêu tam giác mà các đỉnh của tam giác được lấy từ 5 điểm A, B, C, D, E?

Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. Gọi M là trung điểm của CD. Tìm giao điểm E của SD và mặt phẳng IJM.

Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm tam giác ABA’ và M là điểm tùy ý trên đường thẳng B’C’. Đường thẳng MG cắt mặt phẳng (ABC) tại điểm N. Tỉ số \(\frac{{GM}}{{GN}}\) bằng

Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại D và E. a) Chứng minh CD vuông góc với AB, BE vuông góc với AC. b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.

Hiệu 2 số là 66,8. Nếu dịch dấu phẩy của số bé sang trái một hàng thì hiệu mới là 117,83. Tìm số lớn.

Rô-bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để Rô-bốt lấy được 100 ml nước từ chậu nước?

Cho biểu thức \[P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\]. a) Tìm x nguyên để P nhận giá trị nguyên. b) Tìm x sao cho P > 1.

Cho 2 tập khác rỗng A = (m – 1; 4]; B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ⊂ B.

Tìm số tự nhiên a, b biết ƯCLN(a, b) = 4 và a + b = 48.

Cho tam giác ABC. Tìm điểm M sao cho \(\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} = \vec 0\).

Đơn giản biểu thức sau khi bỏ ngoặc: a) –a – (b – a – c); b) – (a – c) – (a – b + c); c) b – (b + a – c); d) –(a – b + c) – (a + b + c); e) (a + b) – (a – b) + (a – c) – (a + c); g) (a + b – c) + (a – b + c) – (b + c – a) – (a – b – c).

Đơn giản biểu thức sau khi bỏ dấu ngoặc: a) (a + b – c) – (b – c + d); b) –(a – b + c) + (a – b + d); c) (a + b) – (–a + b – c); d) –(a + b) + (a + b + c); e) (a – b + c) – (a – b + c); f) –(a – b – c) + (a – b – c).

Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh: a) ∆ADB = ∆ADC. b) AD là tia phân giác của \(\widehat {BAC}\) và \(\widehat B = \widehat C\). c) AD vuông góc với BC.

Số đối của 24 là gì?

Tìm x biết: a) (x – 5).(x + 4) = 0; b) x2 – 7x = 0; c) x2 = –5x; d) x3 = x; e) (x – 5).(x – 4) = 0.

Cho 3x2 + 3y2 = 10xy với y > x > 0. Tính giá trị của biểu thức \(K = \frac{{x + y}}{{x - y}}\).

Giải phương trình 5sin2x + 3sinxcosx – 4cos2x = 2.

Cho các tập hợp A = {x ∈ ℝ | x ≤ a}; B = {x ∈ ℝ | x ≥ b}; C = [–5; 5]. Biết rằng A ∩ C; B ∩ C là các đoạn có độ dài lần lượt là 7 và 9. Tìm tập A ∩ B.

Cho \(A = \sqrt {{{2018}^2} + {{2018}^2}{{.2019}^2} + {{2019}^2}} \). Chứng minh A là một số tự nhiên.

Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n3 – 4n2 + 4n – 1.

Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.

Tìm x biết: x4 + 2x3 – 6x – 9 = 0.

Giải phương trình \(\cos \left( {2x + \frac{\pi }{4}} \right) = \frac{1}{2},\,\, - \pi < x < \pi \).

Giải phương trình \(\cos \left( {2x - \frac{\pi }{4}} \right) = \frac{1}{2}\).

Giải phương trình cos2x – 3cosx + 2 = 0.

Khi chuyển hỗn số \(34\frac{6}{x}\) về dạng phân số thì ta được phân số tối giản A có tổng tử số và mẫu số là 461. Giá trị của x là bao nhiêu?

Cho \(Q = \left( {\frac{1}{{x - 4}} - \frac{1}{{x + 4\sqrt x + 4}}} \right).\frac{{x + 2\sqrt x }}{{\sqrt x }}\). a) Tìm điều kiện xác định của biểu thức Q. b) Rút gọn Q.

Rút gọn biểu thức sau: \(B = \left( {\frac{1}{{x - 4}} - \frac{1}{{x - 4\sqrt x + 4}}} \right).\frac{{x + 2\sqrt x }}{{\sqrt x }}\).

Giải phương trình lượng giác: sin22x + sin24x = sin26x.

Giải phương trình sau: \({\sin ^2}2x = \frac{1}{2}\).

Tìm x biết: \(\sqrt {16x} - 2\sqrt {36x} + 3\sqrt {9x} = 2\).

Cho mười chữ số 0, 1, 2, 3, …, 9. Có bao nhiêu số tự nhiên lẻ gồm 6 chữ số khác nhau, nhỏ hơn 600000 được xây dựng từ 10 số trên.

Tìm tổng của số lẻ nhỏ nhất có ba chữ số khác nhau với số chẵn lớn nhất gồm 2 chữ số chẵn khác nhau.

Tính tổng sau: 1 + 2 + 3 + … + 99.

Tìm nghiệm nguyên của phương trình: 7(x2 + xy + y2) = 39(x + y).

Giải phương trình \(\frac{{m!\,\, - \left( {m - 1} \right)!}}{{\left( {m + 1} \right)!}} = \frac{1}{6}\).

Nếu \(C_n^{12} = C_n^8\) thì \(C_n^{17}\) bằng bao nhiêu?

Phương trình \(\sin \left( {2x + \frac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi:

Giải phương trình: x3(x2 – 7)2 – 36x = 0.

Tìm x, biết: \(\left( {x - \frac{2}{7}} \right)\left( {x + \frac{3}{4}} \right) = 0\).

Tìm nghiệm x thuộc [0; 2π] của phương trình \(5\left( {\sin x + \frac{{\cos 3x + \sin 3x}}{{1 + 2\sin 2x}}} \right) = \cos 2x + 3\).

Nghiệm của phương trình \[A_x^{10} + A_x^9 = 9A_x^8\] là:

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: a) A = cos4x – cos2x + sin2x; b) B = sin4x – sin2x + cos2x.

Cho tam giác ABC, hai điểm M, N được xác định bởi \(3\overrightarrow {MA} + 4\overrightarrow {MB} = \vec 0\); \(\overrightarrow {NB} - 3\overrightarrow {NC} = \vec 0\). Chứng minh 3 điểm M, G, N thẳng hàng, với G là trọng tâm tam giác ABC.

Cho các đa thức sau: A = x3 + 4x2 + 3x – 7 và B = x + 4. a) Tính A : B. b) Tìm x ∈ ℤ sao cho A chia hết cho B.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC cắt AB, AC theo thứ tự tại D và E.

a) Chứng minh CD vuông góc với AB, BE vuông góc với AC.

b) Gọi K là giao điểm của BE và CD. Chứng minh AK vuông góc với BC.

Cho biểu thức \[P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\].

a) Tìm x nguyên để P nhận giá trị nguyên.

b) Tìm x sao cho P > 1.

Đơn giản biểu thức sau khi bỏ dấu ngoặc:

a) (a + b – c) – (b – c + d);

b) –(a – b + c) + (a – b + d);

c) (a + b) – (–a + b – c);

d) –(a + b) + (a + b + c);

e) (a – b + c) – (a – b + c);

f) –(a – b – c) + (a – b – c).

Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh:

a) ∆ADB = ∆ADC.

b) AD là tia phân giác của \(\widehat {BAC}\) và \(\widehat B = \widehat C\).

c) AD vuông góc với BC.

Tìm x biết:

a) (x – 5).(x + 4) = 0;

b) x² – 7x = 0;

c) x² = –5x;

d) x³ = x;

e) (x – 5).(x – 4) = 0.

Cho 3x² + 3y² = 10xy với y > x > 0. Tính giá trị của biểu thức \(K = \frac{{x + y}}{{x - y}}\).

Giải phương trình 5sin²x + 3sinxcosx – 4cos²x = 2.

Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n³ – 4n² + 4n – 1.

Tìm x biết: x⁴ + 2x³ – 6x – 9 = 0.

Cho \(Q = \left( {\frac{1}{{x - 4}} - \frac{1}{{x + 4\sqrt x + 4}}} \right).\frac{{x + 2\sqrt x }}{{\sqrt x }}\).

a) Tìm điều kiện xác định của biểu thức Q.

b) Rút gọn Q.

Giải phương trình lượng giác: sin²2x + sin²4x = sin²6x.

Tìm nghiệm nguyên của phương trình: 7(x² + xy + y²) = 39(x + y).

Giải phương trình: x³(x² – 7)² – 36x = 0.

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:

a) A = cos⁴x – cos²x + sin²x;

b) B = sin⁴x – sin²x + cos²x.

Cho các đa thức sau: A = x³ + 4x² + 3x – 7 và B = x + 4.

a) Tính A : B.

b) Tìm x ∈ ℤ sao cho A chia hết cho B.