5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 78)

\[\left\{ {\begin{array}{*{20}{c}}{{{(x + y)}^2}\left( {8{x^2} + 8{y^2} + 4xy - 13} \right) + 5 = 0}\\{2x + \frac{1}{{x + y}} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{8{x^2} + 8{y^2} + 4xy - 13 + \frac{5}{{{{(x + y)}^2}}} = 0\,}\\{x + y + \frac{1}{{x + y}} + x - y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5\left( {{x^2} + 2xy + {y^2}} \right) + 3\left( {{x^2} - 2xy + {y^2}} \right) + \frac{5}{{{{(x + y)}^2}}} = 13}\\{x + y + \frac{1}{{x + y}} + x - y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{{\left( {x + y} \right)}^2} + \frac{5}{{{{(x + y)}^2}}} + 3{{\left( {x - y} \right)}^2} = 13}\\{x + y + \frac{1}{{x + y}} + x - y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{{\left( {x + y + \frac{1}{{x + y}}} \right)}^2} + 3{{\left( {x - y} \right)}^2} = 23}\\{x + y + \frac{1}{{x + y}} + x - y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Đặt \[x + y + \frac{1}{{x + y}} = a;\,\,\,x - y = b\,\,\,\,\,\,\]

Ta có: \[\left( {\frac{{ - 5}}{4};\,\frac{9}{4}} \right)\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{a^2} - 6a + 3 = 23}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{8{a^2} - 6a - 20 = 0}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(a - 2)(4a + 5) = 0}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = - 1}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{4}}\\{b = \frac{9}{4}}\end{array}} \right.}\end{array}} \right.\]

• Với \[\left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = - 1}\end{array}} \right.\], ta có:

\[\left\{ {\begin{array}{*{20}{c}}{x + y + \frac{1}{{x + y}} = 2}\\{x - y = - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {x + y} \right)}^2} - 2(x + y) + 1 = 0}\\{x - y = - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{(x + y - 1)}^2} = 0}\\{x - y = - 1\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = 1}\end{array}} \right.\]

• Với \[\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{4}}\\{b = \frac{9}{4}}\end{array}} \right.\], ta có:

\[\left\{ {\begin{array}{*{20}{c}}{x + y + \frac{1}{{x + y}} = \frac{{ - 5}}{4}}\\{x - y = \frac{9}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {x + y + \frac{5}{8}} \right)}^2} + \frac{{39}}{{64}} = 0}\\{x - y = \frac{9}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\] (2)

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {x + y} \right)}^2} + 2 \cdot \frac{5}{8}(x + y) + \frac{{25}}{{64}} + \frac{{39}}{{64}} = 0}\\{x - y = \frac{9}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{\left( {x + y + \frac{5}{8}} \right)}^2} + \frac{{39}}{{64}} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x - y = \frac{9}{4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Vì \[{\left( {x + y + \frac{5}{8}} \right)^2} + \frac{{39}}{{64}} > 0,\,\,\forall m\] nên không có giá trị m thoả mãn hệ phương trình (2)

Vậy nghiệm (x; y) của hệ phương trình là (0; 1).

Câu 2

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Xem đáp án

Lời giải

\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{{(1 - a)}^2} = 23}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{a^2} - 6a + 3 = 23}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{8{a^2} - 6a - 20 = 0}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{(a - 2)(4a + 5) = 0}\\{b = 1 - a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = - 1}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{a = \frac{{ - 5}}{4}}\\{b = \frac{9}{4}}\end{array}} \right.}\end{array}} \right.\]

Vậy các nghiệm (a; b) của hệ phương trình là: (2; –1) và \[\left( {\frac{{ - 5}}{4};\,\frac{9}{4}} \right)\].

Câu 3

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

Xem đáp án

Lời giải

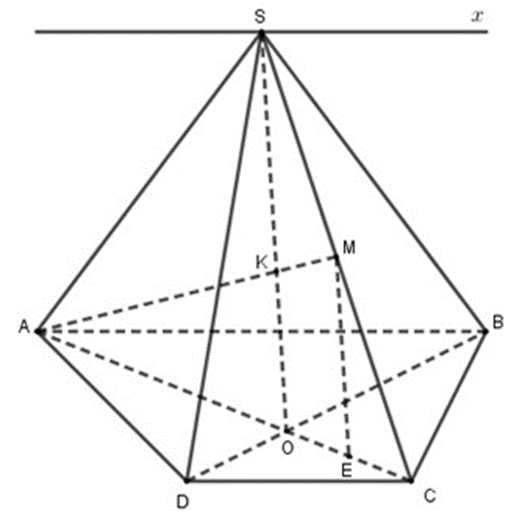
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD (ảnh 1)

S là điểm chung của (SAB) và (SCD).

Kẻ Sx // AB // CD

Ta có: AB // CD

AB ⊂ (SAB)

CD ⊂ (SCD)

Suy ra (SAB) ∩ (SCD) = {Sx}

Vậy giao tuyến của hai mặt phẳng (SAB) và (SCD) là Sx.

Câu 4

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Xem đáp án

Lời giải

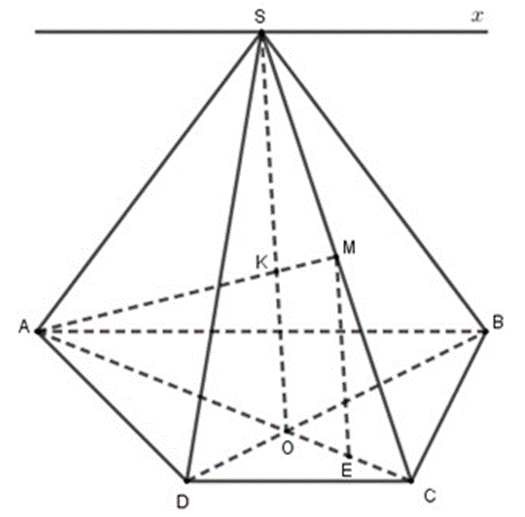
Ta có: AM ⊂ (SAC)

Dễ thấy S ∈ (SAC) ∩ (SBD)

Gọi O là giao điểm của AC và BD

Khi đó O ∈ AC⊂ (SAC),

O ∈ BD ⊂ (SBD)

Do đó O ∈ (SAC) ∩ (SBD)

Þ SO = (SAC) ∩ (SBD)

Trong (SAC) gọi AM ∩ SO = {K}

Ta có: K ∈ AM, K ∈ SO ⊂ (SBD)

Þ AM ∩ (SBD) = {K},

Vậy giao điểm K của đường thẳng AM với (SBD) là giao điểm của AM và SO.

Câu 5

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.

Xem đáp án

Lời giải

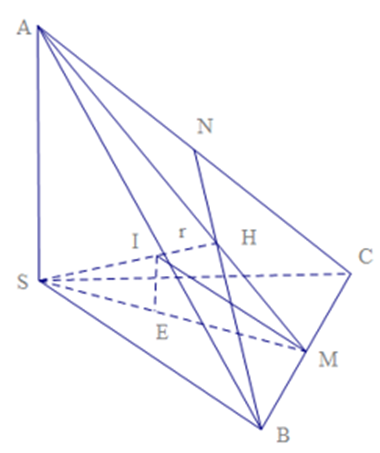
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với (ảnh 1)

Áp dụng công thức \[r = \frac{{3V}}{{{S_{tp}}}}\,\,\] (*) và tam giác đều cạnh x có diện tích \[S = \frac{{{x^2}\sqrt 3 }}{4}\,\,\]

Từ giả thiết S.ABC đều có SA = SB = SC. Lại có SA, SB, SC đôi một vuông góc và thể tích khối chóp S.ABC bằng \[\frac{{{a^3}}}{6}\]nên ta có SA = SB = SC = a.

Suy ra \[AB = BC = CA = a\sqrt 2 \] và tam giác ABC đều cạnh có độ dài \[a\sqrt 2 \]. Do đó diện tích toàn phần của khối chóp S.ABC là

S_tp = S_SAB + S_SBC+ S_SCA + S_ABC

\[ = \frac{{3{a^2}}}{2} + \frac{{{{\left( {a\sqrt 2 } \right)}^2}.\sqrt 3 }}{4} = \frac{{{a^2}\left( {3 + \sqrt 3 } \right)}}{2}\]

Thay vào (*) ta được: \[\frac{{4\pi }}{3}\].

Vậy r = \[r = \frac{a}{{3 + \sqrt 3 }}\].

Câu 6

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 78)

🔥 Đề thi HOT:

20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)

124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án

56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

Danh sách câu hỏi:

Giải hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{{{(x + y)}^2}\left( {8{x^2} + 8{y^2} + 4xy - 13} \right) + 5 = 0}\\{2x + \frac{1}{{x + y}} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Giải hệ phương trình: \[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng \[\frac{{{a^3}}}{6}\]. Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).

Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E; CF cắt BE tại H. Chứng minh tứ giác AEHF nội tiếp.

Cho tam giác ABC có \[\widehat B = 60^\circ \], BC = 8 cm, AB+AC= 12 cm. Tính độ dài AB, AC.

Cho tam giác ABC có \[\widehat B = 60^\circ \], BC = 10 cm. Chu vi của tam giác ABC là 24 cm. Tính độ dài AB, AC.

Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Chứng minh AH = DE.

Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE. Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.

Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AC. Trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh ΔMAC = ΔNAE.

Cho tam giác ABC. Trên tia đối của tia AB lấy D sao cho AD = AC. Trên tia đối của AC lấy E sao cho AE = AB. Gọi M và N lần lượt là trung điểm của BE và CD. Chứng minh M; A; N thẳng hàng.

Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I. Chứng minh: CO ⊥ AD.

Số các ước tự nhiên của 252 là bao nhiêu? Liệt kê các ước của 252.

Tìm các ước nguyên tố của 36.

Tìm số \[\overline {abcdef} \] (d ¹ 0) sao cho \[\overline {abcdef} = 999.\,\overline {abc} + 200\].

Cho tam giác ABC, kẻ AH ^ BC. Trên tia đối của tia HA, lấy điểm K sao cho HK = HA. Nối KB, KC. Tìm các cặp tam giác bằng nhau trong hình vẽ.

Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Chứng minh: ΔABH = ΔDBH.

Tìm các hệ số a, b, c sao cho đa thức 3x4 + ax2 + bx + c chia hết cho đa thức (x – 2) và chia cho đa thức (x2 – 1) được thương và còn dư (−7x – 1).

Tìm a, b, c để đa thức f(x) = x3 + ax2 + bx + c chia hết cho x − 2 và chia cho x2 − 1 thì dư 2x.

Tìm số có 2 chữ số biết rằng nếu viết thêm chữ số 0 vào vào giữa 2 chữ số của số đó thì ta được số mới gấp 7 lần số phải tìm.

Tìm số có hai chữ số biết rằng nếu viết chữ số 3 vào giữa hai chữ số đó ta được một số có 3 chữ số gấp 11 lần số cần tìm?

Cho x + y + z = 1. Chứng minh: \[{x^2} + {y^2} + {z^2} \ge \frac{1}{3}\].

Cho (x + y + z)2 = x2 + y2 + z2. Chứng minh rằng: \[\frac{1}{{{x^3}}} + \frac{1}{{{y^3}}} + \frac{1}{{{z^3}}} = \frac{3}{{xyz}}\]

Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.

Cho p, q là số nguyên tố và phương trình x2 − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Tìm các số nguyên tố p và q sao cho 7p + q và pq + 11 cũng là các số nguyên tố.

Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.

Cho x, y là các số dương thỏa mãn 4xy = x + y + 2. Tìm giá trị nhỏ nhất của biểu thức \[x + y + \frac{1}{{x + y}}\]

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Chứng minh rằng OA vuông góc với BC.

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

Giải phương trình: \[{x^2} + 6x + 1 = (2x + 1)\sqrt {{x^2} + 2x + 3} \].

Từ các chữ số 0, 1, 2, 3, 5 có thể lập được bao nhiêu số tự nhiên không chia hết cho 5, gồm 4 chữ số khác nhau?

Từ các chữ số 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên chia hết cho 6, gồm ba chữ số đôi một khác nhau?

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.

Tìm tập hợp bội của 6.

Xác định parabol (P): y = ax2 + bx + 2, biết rằng (P) đi qua hai điểm M (1; 5) và N (−2; 8).

Cho parabol (P): y = ax2 + bx + c có trục đối xứng là đường thẳng x = 1. Tính 4a + 2b.

Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?

Tìm số nguyên n để n3 – 3 chia hết cho n − 2.

Tìm số nguyên n để n2 + 3n + 3 chia hết cho 2n + 1.

Phân tích đa thức thành nhân tử: x3 – x2y – xy2 + y3.

Phân tích đa thức thành nhân tử: –6x2 – 9xy + 15y2.

Tính nhanh: 95,72 ´ 3,57 + 3,57 ´ 4,28

Tính nhanh: 17,8 ´ 99 + 17 + 0,8.

Trong các số sau số nào là số nguyên tố: 20; 31; 45?

Chứng minh 6 không phải là số nguyên tố.

Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài tăng 2 lần, chiều rộng không đổi?

Diện tích hình chữ nhật thay đổi như thế nào nếu: Chiều dài và chiều rộng tăng 3 lần?

Xác định parabol (P): y = ax2 + bx + 4 có trục đối xứng là đường thẳng \[x = \frac{1}{3}\] và đi qua điểm A(1; 3).

Cho parabol (P): y = ax2 + bx + 2. Xác định hệ số a, b biết (P) có đỉnh I(2; – 2).

Cho hàm số: y = x-4. Tìm khẳng định sai.

Cho đường thẳng (d) có hàm số: y = (k – 3) + k' đi qua điểm A(1; 2); B(– 3; 4). Tìm k, k’.

Rút gọn biểu thức: \[3\sqrt 5 a - \sqrt {20} a + 4\sqrt {45} a + \sqrt a \] với a ≥ 0.

Rút gọn biểu thức: \[5\sqrt {\frac{1}{5}} + \frac{1}{{20}}\sqrt {20} + \sqrt 5 \]

Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto \[\overrightarrow {GG'} \].

Cho các số dương x, y, z thỏa mãn x + y + z = 1. Tìm giá trị nhỏ nhất của biểu thức: \[d(BD;SC) = OK = \frac{1}{2}d(A;SC) = \frac{1}{2} \cdot \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }}\]

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{{{(x + y)}^2}\left( {8{x^2} + 8{y^2} + 4xy - 13} \right) + 5 = 0}\\{2x + \frac{1}{{x + y}} = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Giải hệ phương trình:

\[\left\{ {\begin{array}{*{20}{c}}{5{a^2} + 3{b^2} = 23}\\{a + b = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]

Tìm các hệ số a, b, c sao cho đa thức 3x⁴+ ax²+ bx + c chia hết cho đa thức (x – 2) và chia cho đa thức (x²– 1) được thương và còn dư (−7x – 1).

Tìm a, b, c để đa thức f(x) = x³ + ax² + bx + c chia hết cho x − 2 và chia cho x² − 1 thì dư 2x.

Cho (x + y + z)² = x² + y²+ z².

Chứng minh rằng: \[\frac{1}{{{x^3}}} + \frac{1}{{{y^3}}} + \frac{1}{{{z^3}}} = \frac{3}{{xyz}}\]

Cho p, q là số nguyên tố và phương trình x² − px + q = 0 có nghiệm nguyên dương. Tìm p, q.

Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x² + y².

Xác định parabol (P): y = ax² + bx + 2, biết rằng (P) đi qua hai điểm

M (1; 5) và N (−2; 8).

Cho parabol (P): y = ax² + bx + c có trục đối xứng là đường thẳng x = 1.

Tính 4a + 2b.

Tìm số nguyên n để n³ – 3 chia hết cho n − 2.

Tìm số nguyên n để n² + 3n + 3 chia hết cho 2n + 1.

Phân tích đa thức thành nhân tử: x³ – x²y – xy² + y³.

Phân tích đa thức thành nhân tử: –6x² – 9xy + 15y².

Xác định parabol (P): y = ax² + bx + 4 có trục đối xứng là đường thẳng \[x = \frac{1}{3}\] và đi qua điểm A(1; 3).

Cho parabol (P): y = ax² + bx + 2. Xác định hệ số a, b biết (P) có đỉnh I(2; – 2).

Cho hàm số: y = x^-4. Tìm khẳng định sai.

Biết đa thức f(x) = x³+ ax² + bx + 2 chia cho x + 1 dư 5, chia cho x + 2 dư 8. Khi đó

Biết đa thức f(x) = x³+ ax + b chia cho x – 2 dư 3, chia cho x – 3 dư 5. Tìm đa thức đó.