5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 70)

Khi đó ta có \(\left( {x + y + z} \right)\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right) \ge 3\sqrt[3]{{xyz}}.\frac{3}{{\sqrt[3]{{xyz}}}} = 9\).

\( \Leftrightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \ge \frac{9}{{x + y + z}}\).

Dấu “=” xảy ra khi và chỉ khi x = y = z.

Vậy ta có điều phải chứng minh.

Câu 2

Cho tam giác ABC có các góc thỏa mãn \(\frac{{\sin A}}{1} = \frac{{\sin B}}{2} = \frac{{\sin C}}{{\sqrt 3 }}\). Tính số đo các góc của tam giác.

Xem đáp án

Lời giải

Áp dụng định lí sin cho tam giác ABC, ta được: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).

Suy ra \(\sin A = \frac{a}{{2R}};\,\,\sin B = \frac{b}{{2R}};\,\,\sin C = \frac{c}{{2R}}\).

Theo đề, ta có: \(\frac{{\sin A}}{1} = \frac{{\sin B}}{2} = \frac{{\sin C}}{{\sqrt 3 }}\).

\( \Rightarrow \frac{{\frac{a}{{2R}}}}{1} = \frac{{\frac{b}{{2R}}}}{2} = \frac{{\frac{c}{{2R}}}}{{\sqrt 3 }} \Rightarrow \frac{a}{1} = \frac{b}{2} = \frac{c}{{\sqrt 3 }}\).

Đặt \(\frac{a}{1} = \frac{b}{2} = \frac{c}{{\sqrt 3 }} = t\).

Suy ra a = t; b = 2t; \(c = t\sqrt 3 \).

Khi đó a² = t²; b² = 4t²; c² = 3t².

Ta thấy t² + 3t² = 4t².

Suy ra a² + c² = b².

Áp dụng định lí Pythagore đảo, ta có tam giác ABC vuông tại B.

Do đó sinB = 1.

Vì vậy \(\frac{{\sin A}}{1} = \frac{1}{2} = \frac{{\sin C}}{{\sqrt 3 }}\).

Suy ra \(\left\{ \begin{array}{l}\sin A = \frac{1}{2}\\\sin C = \frac{{\sqrt 3 }}{2}\end{array} \right.\)

Do đó \(\left\{ \begin{array}{l}\widehat A = 30^\circ \\\widehat C = 60^\circ \end{array} \right.\)

Vậy \(\widehat A = 30^\circ ;\,\,\widehat B = 90^\circ ;\,\,\widehat C = 60^\circ \).

Câu 3

Cho \(\left( {x + \sqrt {2005 + {x^2}} } \right)\left( {y + \sqrt {2005 + {y^2}} } \right) = 2005\). Tính x²⁰⁰⁵ + y²⁰⁰⁵.

Xem đáp án

Lời giải

Ta có \(\left( {x + \sqrt {2005 + {x^2}} } \right)\left( {\sqrt {2005 + {x^2}} - x} \right) = 2005 + {x^2} - {x^2} = 2005\).

Theo đề, ta có \(\left( {x + \sqrt {2005 + {x^2}} } \right)\left( {y + \sqrt {2005 + {y^2}} } \right) = 2005\).

\( \Leftrightarrow \left( {x + \sqrt {2005 + {x^2}} } \right)\left( {y + \sqrt {2005 + {y^2}} } \right) = \left( {x + \sqrt {2005 + {x^2}} } \right)\left( {\sqrt {2005 + {x^2}} - x} \right)\).

\( \Leftrightarrow y + \sqrt {2005 + {y^2}} = \sqrt {2005 + {x^2}} - x\) (1)

Chứng minh tương tự, ta được: \(x + \sqrt {2005 + {x^2}} = \sqrt {2005 + {y^2}} - y\) (2)

Lấy (1) + (2) cộng vế theo vế, ta được:

\(x + \sqrt {2005 + {x^2}} + y + \sqrt {2005 + {y^2}} = \sqrt {2005 + {x^2}} - x + \sqrt {2005 + {y^2}} - y\).

⇔ x + y = –x – y.

⇔ 2(x + y) = 0.

⇔ x + y = 0.

Ta có x²⁰⁰⁵ + y²⁰⁰⁵ = (x + y)(x²⁰⁰⁴ – x²⁰⁰³.y + x²⁰⁰².y² – ... + x².y²⁰⁰² – x.y²⁰⁰³ + y²⁰⁰⁴).

= 0.(x²⁰⁰⁴ – x²⁰⁰³.y + x²⁰⁰².y² – ... + x².y²⁰⁰² – x.y²⁰⁰³ + y²⁰⁰⁴).

= 0.

Vậy x²⁰⁰⁵ + y²⁰⁰⁵ = 0.

Câu 4

Rút gọn biểu thức \(A = \left( {\frac{{x + 2}}{{\sqrt x + 1}} - \sqrt x } \right):\left( {\frac{{\sqrt x - 4}}{{1 - x}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\).

Xem đáp án

Lời giải

Ta có \(A = \left( {\frac{{x + 2}}{{\sqrt x + 1}} - \sqrt x } \right):\left( {\frac{{\sqrt x - 4}}{{1 - x}} - \frac{{\sqrt x }}{{\sqrt x + 1}}} \right)\)

\( = \frac{{x + 2 - \sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}:\frac{{\sqrt x - 4 - \sqrt x \left( {1 - \sqrt x } \right)}}{{\left( {1 - \sqrt x } \right)\left( {1 + \sqrt x } \right)}}\)

\( = \frac{{x + 2 - x - \sqrt x }}{1}.\frac{{1 - \sqrt x }}{{\sqrt x - 4 - \sqrt x + x}}\)

\[ = \frac{{\left( {2 - \sqrt x } \right)\left( {1 - \sqrt x } \right)}}{{x - 4}} = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\].

Câu 5

Cho (O; R) và (O’; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O’) sao cho AM vuông góc với AN.

a) Chứng minh OM // O’N.

b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.

Xem đáp án

Lời giải

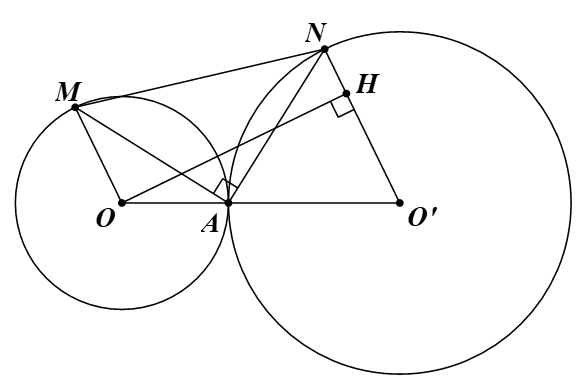
Cho (O; R) và (O’; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung (ảnh 1)

a) Vì OM = OA = R nên tam giác OAM cân tại O.

Suy ra \(\widehat {AOM} = 180^\circ - 2.\widehat {OAM}\).

Chứng minh tương tự, ta được \(\widehat {AO'N} = 180^\circ - 2.\widehat {O'AN}\).

Ta có \(\widehat {OAM} + \widehat {MAN} + \widehat {NAO'} = 180^\circ \) (kề bù).

Suy ra \(\widehat {OAM} + \widehat {NAO'} = 180^\circ - \widehat {MAN} = 180^\circ - 90^\circ = 90^\circ \).

Ta có \(\widehat {AOM} + \widehat {AO'N} = 180^\circ - 2.\widehat {OAM} + 180^\circ - 2.\widehat {O'AN}\).

\( = 360^\circ - 2.\left( {\widehat {OAM} + \widehat {O'AN}} \right) = 360^\circ - 2.90^\circ = 180^\circ \).

Mà hai góc \(\widehat {AOM},\widehat {AO'N}\) ở vị trí trong cùng phía.

Vậy OM // O’N.

b) Gọi H là hình chiếu vuông góc của O lên O’N.

Vì OM // O’N nên tứ giác OMNO’ là hình thang.

Suy ra \({S_{OMNO'}} = \frac{{OH.\left( {OM + O'N} \right)}}{2} = \frac{{OH.\left( {R + R'} \right)}}{2}\).

\[ \le \frac{{OO'.\left( {R + R'} \right)}}{2} = \frac{{\left( {R + R'} \right).\left( {R + R'} \right)}}{2} = \frac{{{{\left( {R + R'} \right)}^2}}}{2}\].

Dấu “=” xảy ra ⇔ H ≡ O’ hay OO’ ⊥ O’N, OO’ ⊥ OM.

Khi đó \(\widehat {AOM} = 90^\circ \). Suy ra \(\widehat {OAM} = 45^\circ \).

Chứng minh tương tự, ta được \(\widehat {O'AN} = 45^\circ \).

Vậy M ở vị trí sao cho tam giác OAM vuông cân tại O, N ở vị trí sao cho tam giác O’AN vuông cân tại O’ thì diện tích tứ giác OMNO’ lớn nhất.

Câu 6

Tìm số nguyên dương n,biết: 16 ≤ 8ⁿ ≤ 64.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử