5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 23)

82 người thi tuần này 4.6 60.1 K lượt thi 118 câu hỏi 50 phút

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41
Đề số 42
Đề số 43
Đề số 44
Đề số 45
Đề số 46
Đề số 47
Đề số 48
Đề số 49
Đề số 50
Đề số 51
Đề số 52
Đề số 53
Đề số 54
Đề số 55
Đề số 56
Đề số 57
Đề số 58
Đề số 59
Đề số 60
Đề số 61
Đề số 62
Đề số 63
Đề số 64
Đề số 65
Đề số 66
Đề số 67
Đề số 68
Đề số 69
Đề số 70
Đề số 71
Đề số 72
Đề số 73
Đề số 74
Đề số 75
Đề số 76
Đề số 77
Đề số 78
Đề số 79
Đề số 80
Đề số 81
Đề số 82
Đề số 83
Đề số 84
Đề số 85

🔥 Đề thi HOT:

2867 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

62.5 K lượt thi 126 câu hỏi

2316 người thi tuần này

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

15.3 K lượt thi 35 câu hỏi

1379 người thi tuần này

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

14 K lượt thi 20 câu hỏi

1374 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

13.1 K lượt thi 20 câu hỏi

1337 người thi tuần này

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

13.4 K lượt thi 40 câu hỏi

1307 người thi tuần này

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

16 K lượt thi 35 câu hỏi

1287 người thi tuần này

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

20.5 K lượt thi 25 câu hỏi

1042 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

9.8 K lượt thi 15 câu hỏi

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

19317 lượt thi

8 đề

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

15177 lượt thi

8 đề

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

16437 lượt thi

7 đề

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

14828 lượt thi

7 đề

225 Bài tập Số phức ôn thi Đại học có lời giải

11231 lượt thi

8 đề

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

23358 lượt thi

10 đề

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

20815 lượt thi

9 đề

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

13053 lượt thi

8 đề

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

7556 lượt thi

7 đề

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

6233 lượt thi

3 đề

Danh sách câu hỏi:

Câu 1

Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.

a) Chứng minh rằng AP.AQ = AI².

Xem đáp án

Lời giải

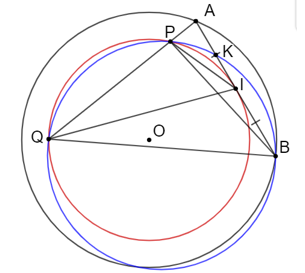
Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua (ảnh 1)

a) Ta có:

$\hat{A I P} = \hat{P Q I}$ (góc tạo bởi tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung IP)

$\Rightarrow \hat{A I P} = \hat{A Q I}$

Xét ∆AIP và ∆AQI có:

$\hat{A I P} = \hat{A Q I}$ (cmt)

$\hat{A}$ : góc chung

Þ ∆AIP ᔕ ∆AQI (g.g)

$\Rightarrow \frac{A I}{A Q} = \frac{A P}{A I} \Rightarrow A P . A Q = A I^{2}$ (1) (đpcm)

Câu 2

b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh

rằng AK.AB = AP.AQ.

Xem đáp án

Lời giải

b. Ta có:

$\hat{P Q K} = \hat{K B P}$ (Hai góc nội tiếp cùng chắn cung PK)

$\Rightarrow \hat{A Q K} = \hat{A B P}$

Xét ∆AQK và ∆ABP có:

$\hat{A Q K} = \hat{A B P}$ (cmt)

$\hat{A}$ : góc chung

Þ ∆AQK ᔕ ∆ABP (g.g)

$\Rightarrow \frac{A Q}{A B} = \frac{A K}{A P} \Rightarrow A K . A B = A P . A Q$ (2) (đpcm)

Câu 3

c) Chứng minh rằng K là trung điểm của AI.

Xem đáp án

Lời giải

c. Từ (1) và (2) suy ra $A K . A B = A I^{2} (= A P . A Q)$

Mà I là trung điểm của AB nên $A K . 2 A I = A I^{2} \Leftrightarrow 2 A K = A I$ .

Vậy K là trung điểm của AI.

Câu 4

Cho đường tròn (C) tâm O với I là trung điểm của dây AB không đi qua O. Một đường thẳng thay đổi đi qua A cắt đường tròn (C₁) tâm O bán kính OI tại P và Q. Chứng minh rằng:

a) Tích AP.AQ không đổi.

Xem đáp án

Lời giải

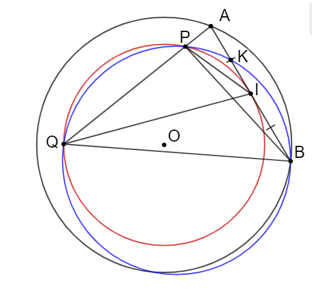
Cho đường tròn (C) tâm O với I là trung điểm của dây AB không đi qua O. Một đường thẳng thay đổi đi qua A cắt đường tròn (C1) (ảnh 1)

a) Ta có:

$\hat{A I P} = \hat{P Q I}$ (Góc tạo bởi tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung IP)

$\Rightarrow \hat{A I P} = \hat{A Q I}$

Xét ∆AIP và ∆AQI có:

$\hat{A I P} = \hat{A Q I}$ (cmt)

$\hat{A}$ : góc chung

Þ ∆AIP ᔕ ∆AQI (g.g)

$\Rightarrow \frac{A I}{A Q} = \frac{A P}{A I} \Rightarrow A P . A Q = A I^{2}$ (1)

Mà AI là cố định nên tích AP.AQ không đổi.

Câu 5

b) Đường tròn ngoại tiếp tam giác BPQ luôn đi qua một điểm cố định khác B.

Xem đáp án

Lời giải

b. Lấy điểm K sao cho K khác B là giao điểm của đường tròn ngoại tiếp tam giác BPQ và đoạn thẳng AB.

Ta có:

$\hat{P Q K} = \hat{K B P}$ (Hai góc nội tiếp cùng chắn cung PK)

$\Rightarrow \hat{A Q K} = \hat{A B P}$

Xét ∆AQK và ∆ABP có:

$\hat{A Q K} = \hat{A B P}$ (cmt)

$\hat{A}$ : góc chung

Þ ∆AQK ᔕ ∆ABP (g.g)

$\Rightarrow \frac{A Q}{A B} = \frac{A K}{A P} \Rightarrow A K . A B = A P . A Q$ (2)

Từ (1) và (2) suy ra $A K . A B = A I^{2} (= A P . A Q)$

Mà I là trung điểm của AB nên $A K . 2 A I = A I^{2} \Leftrightarrow 2 A K = A I$

Vậy K là trung điểm của AI nên K cố định.

Vậy đường tròn ngoại tiếp tam giác BPQ luôn đi qua một điểm cố định khác B là K.

Câu 6

Cho parabol $(P) : y = \frac{1}{2} x^{2}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n.

a) Tìm tọa độ hai điểm A, B. Tìm m, n biết (d) đi qua hai điểm A, B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

b) Tính độ dài đường cao OH của tam giác OAB. (điểm O là gốc tọa độ).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Cho parabol $(P) : y = \frac{1}{2} x^{2}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n.

a) Tìm tọa độ hai điểm A, B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

b) Tìm m, n biết (d) đi qua hai điểm A, B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho tan a + cot a = m. Tìm m để tan² a + cot² a = 7.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Cho tan a + cot a = m. Tính tan³ a + cot³ a theo m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho biểu thức $A = \frac{x + 2}{x + 3} - \frac{5}{x^{2} + x - 6} + \frac{1}{2 - x}$ .

a) Tìm điều kiện của x để A có nghĩa.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

b) Rút gọn A.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

c) Tìm x để $A = \frac{- 3}{4}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

d) Tìm x để biểu thức A có giá trị nguyên

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

e) Tìm giá trị của A khi x² − 9 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho biểu thức $P = \frac{x + 2}{x + 3} - \frac{5}{x^{2} + x - 6} + \frac{1}{2 - x}$ . Tìm x để $P = \frac{- 3}{4}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Tìm số có 3 chữ số, biết rằng nếu bỏ chữ số 0 ở tận cùng bên phải số đó ta được số mới mà hiệu của số mới và số đã cho bằng 135.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Tìm số tự nhiên có 3 chữ số biết rằng nếu viết thêm 1 chữ số 0 vào giữa chữ số hàng trăm và hàng chục của số đó ta được số mới gấp 6 lần số phải tìm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Giải phương trình $9^{x^{2} + x - 1} - {10.3}^{x^{2} + x - 2} + 1 = 0$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Phương trình $9^{x^{2} + x - 1} - {10.3}^{x^{2} + x - 2} + 1 = 0$ có tập nghiệm là

A. {−2; −1; 1; 2};

B. {−2; 0; 1; 2};

C. {−2; −1; 0; 1};

D. {−1; 0; 2}.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho a² + b² + c² = ab + bc + ca. Chứng minh a = b = c.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Cho hình thoi ABCD, có $\hat{A} = 60 °$ . Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh 5 điểm E, F, G, H, B, D cùng thuộc một đường tròn

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh: ∆BAM = ∆CAN.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Chứng minh rằng:

b) MN = BM + CN.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Số nghiệm của phương trình cos 2x + 3sin x − 2 = 0 trên khoảng (0; 20π) là bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Giải phương trình: cos 2x + 3sin x − 2 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Tính sin x, cos x, tan x, cot x biết . $\sin x + \cos x = \sqrt{2}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Cho $\sin x + \cos x = \frac{2}{3}$ . Hãy tính: A = sin x.cos x.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA vuông góc (ABCD), SC hợp với đáy một góc 45° và AB = 3a, BC =4a. Tính thể tích khối chóp.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc với mặt phẳng đáy, SC tạo với đáy một góc 45° và $S C = 2 a \sqrt{2}$ . Thể tích khối chóp S.ABCD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Cho đường tròn (O) tâm O đường kính AB lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn (O) tại điểm C cắt tia OI tại điểm D.

a) Chứng minh OI // BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

b) Chứng minh DA là tiếp tuyến đường tròn (O).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

c) Vẽ CH vuông góc với AB, H thuộc AB và vẻ BK vuông góc với CD, K thuộc CD. Chứng minh: CK² = AH.BH

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\hat{A M B} = 60 °$ . Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\hat{A M B} = 60 °$ . Biết chu vi tam giác MAB là 24 cm, tính độ dài bán kính đường tròn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

A \ B được gọi là phần bù của B trong A khi nào?

A. A Ì B;

B. B Ì A;

C. A Ç B;

D. A È B.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

$|A| - |B| \leq |A - B|$ . Dấu “=” xảy ra khi nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

a) Tìm BC của 4 và 6.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

b) Tìm ƯC của 10 và 20.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Tìm ƯC thông qua tìm ƯCLN: 10; 20 và 70.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Cho biểu thức $P = (\sqrt{x} - \frac{x + 2}{\sqrt{x} + 1}) : (\frac{\sqrt{x}}{\sqrt{x} + 1} - \frac{\sqrt{x} - 4}{1 - x})$ .

a) Rút gọn P.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

b) Tìm giá trị của x để P < 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

c) Tìm GTNN của P.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Cho biểu thức $P = (1 + \frac{\sqrt{a}}{a + 1}) : (\frac{1}{\sqrt{a} - 1} - \frac{2 \sqrt{a}}{a \sqrt{a} + \sqrt{a} - a - 1})$ .

a) Rút gọn P.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

b) Tìm giá trị của a để P < 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

c) Tìm giá trị của P nếu . $a = 19 - 8 \sqrt{3}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Trong mặt phẳng Oxy, cho A(2; 4), B(−1; 4), C(−5; 1). Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(−4; 2), B(2; 4), C(8; −2). Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Từ điểm P nằm ngoài đường tròn (O; R) vẽ 2 tiếp tuyến PA, PB tới (O) với A, B là các tiếp điểm. Vẽ AH vuông góc với đường kính BC. Chứng minh PC cắt AH tại trung điểm I của AH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA, PB tới đường tròn (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A tới đường kính BC, đoạn thẳng PC cắt AH tại E.

a) Chứng minh bốn điểm P, A, O, B cùng nằm trên một đường tròn.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 53

b) Chứng minh OB.AH = CH.PB và E là trung điểm của AH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

c) Giả sử PO = d. Tính AH theo R và d.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 55

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn: $|\vec{M A} + \vec{M C}| = |\vec{M A} - \vec{M B}|$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 56

Cho tam giác ABC. Tìm tập hợp các điểm M trong trường hợp sau: $\vec{M A} = \vec{M B}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 57

Cho phương trình x²− (2m + 5)x + 2m + 1 = 0 với m là tham số có hai nghiệm dương phân biệt x₁, x₂. Tìm m thỏa mãn $|\sqrt{x_{1}} - \sqrt{x_{2}}|$ có giá trị nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 58

Cho phương trình: x² − 2(m − 1)x + 2m − 5 = 0 (1)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biết với mọi m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 59

b) Tìm m để phương trình (1) có 2 nghiệm x₁, x₂ thỏa mãn x₁ < 2 < x₂.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 60

So le ngoài là như thế nào? Lấy ví dụ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 61

Cặp góc so le trong cùng phía; cặp góc so le ngoài cùng phía; cặp góc so le trong; cặp góc đồng vị là gì?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 62

Có bao nhiêu đường tròn đi qua ba điểm thẳng hàng?

A. Vô số đường tròn;

B. Một đường tròn;

C. Hai đường tròn;

D. Không có đường tròn nào.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 63

Có bao nhiêu đường tròn đi qua ba điểm không thẳng hàng?

A. Vô số đường tròn;

B. Một đường tròn;

C. Hai đường tròn;

D. Không có đường tròn nào.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 64

Cho tam giác ABC. Tìm tập hợp điểm M:

. $|\vec{M A} + \vec{M B} + \vec{M C}| = |\vec{M A} + 2 \vec{M B}|$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 65

Cho đường thẳng (d): y = (m + 1)x + 2m − 3. Chứng minh rằng với mọi m đường thẳng (d) luôn luôn đi qua một điểm cố định. Xác định điểm cố định đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 66

Tìm điểm cố định mà đồ thị hàm số y = (m − 1)x + 2m − 3 luôn đi qua

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 67

Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). AC cắt đường tròn (O) tại D (D khác C).

a) Chứng minh: BD ^ AC và AB² = AD.AC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 68

b) Từ C vẽ dây CE // OA; BE cắt OA tại H. Chứng minh H là trung điểm của BE và AE là tiếp tuyến của đường tròn (O).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 69

c) Chứng minh $\hat{O C H} = \hat{O A C}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 70

d) Tia OA cắt đường tròn (O) tại F. Chứng minh FA.CH = HF.CA.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 71

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho

$|2 (\vec{M A} + \vec{M B} + \vec{M C})| = |3 (\vec{M B} + \vec{M C})|$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 72

Cho ∆ABC cân tại A. Kẻ AH ^ BC (H Î BC).

a) Chứng minh HB = HC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 73

b) Kẻ HM ^ AB (M Î BC); HN ^ AC (N Î BC). CMR: ∆HMN là tam giác cân

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 74

c) Chứng minh: MN song song với BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 75

Cho tam giác ABC cân tại A, kẻ AH ⊥ BC. Chứng minh:

a) HB = HC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 76

b) Kẻ HM ^ AB, HN ^ AC. Chứng minh ∆HMB = ∆HNC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 77

c) Chứng minh tam giác AMN cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 78

Tìm điều kiện của x để biểu thức $\frac{3 x - 1}{x^{2} - 4}$ là phân thức.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 79

Cho 6 chữ số 2, 3, 4, 6, 7, 9. Lấy 3 chữ số lập thành số a. Có bao nhiêu số a < 400?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 80

Cho sáu chữ số: 2, 3, 5, 6, 7, 9.

a) Có bao nhiêu số có ba chữ số, các chữ số trong mỗi số đều khác nhau, được lập thành từ các chữ số trên?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 81

b) Trong các số dược thành lập có bao nhiêu số nhỏ hơn 400? Bao nhiêu số là số lẻ? Bao nhiêu số chia hết cho 5?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 82

Từ các chữ số 1, 2 , 3, 4, 5, 7, 8, 9 có thể lập được bao nhiêu số tự nhiên, mỗi số gồm 6 chữ số khác nhau và tổng các chữ số hàng chục, hàng trăm, hàng nghìn bằng 8.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 83

Xác định parabol y = ax²+ bx + c, (a ≠ 0), biết rằng đỉnh của parabol đó có tung độ bằng −25, đồng thời parabol đó cắt trục hoành tại hai điểm A(−4; 0) và B(6; 0).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 84

Xác định parabol (p): y = ax²+ bx + c, (a ≠ 0), biết (p) cắt trục tung tại điểm có tung độ bằng 1 và có giá trị nhỏ nhất bằng $\frac{3}{4}$ khi $x = \frac{1}{2}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 85

Cho hai đường thẳng

(d₁): y = ax + b (a ≠ 0);

(d₂): y = a'x + b' (a' ≠ 0);

(d₁) và (d₂) song song, cắt nhau, trùng nhau khi nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 86

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $(d_{1}) : \{\begin{cases} x = 4 + 2 t \\ y = 1 - 5 t \end{cases}$ và (d₂): 2x − 5y − 14 = 0.

Khẳng định nào sau đây đúng?

A. (d₁), (d₂) song song với nhau;

B. (d₁), (d₂) vuông góc với nhau;

C. (d₁), (d₂) cắt nhưng không vuông góc với nhau;

D. (d₁), (d₂) trùng nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 87

Tìm dư trong phép chia 325 cho 9.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 88

Trong khoảng từ 160 đến 325 có bao nhiêu số chia hết cho 9?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 89

Tìm số hạng thứ 8 trong khai triển (1 − 2x)¹².

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 90

Hệ số của số hạng thứ 8 trong khai triển nhị thức Niu-tơn (2 + 3x)¹⁴.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 91

Cho hàm số y = (m − 1)x + 2 có đồ thị là đường thẳng (d).

a) Tìm m biết (d) đi qua điểm M(2; 1).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 92

b) Viết phương trình của đường thẳng (d') đi qua điểm B(1; 3) và cắt trục tung tại điểm có tung độ bằng 5. Tìm tọa độ giao điểm của (d) và (d') đã tìm được.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 93

Cho hàm số y = (m + 1)x − 2 có đồ thị là đường thẳng (d).

a) Tìm m để đồ thị hàm số (d) cắt đồ thị hàm số y = x + 3 tại điểm tung độ là 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 94

b) Vẽ đồ thị hàm số tìm được ở câu a . Tính diện tích tam giác tạo bởi đồ thị hàm số với hai trục tọa độ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 95

Cho hình chóp S.ABCD. Gọi M, N, P là các điểm trên SA, SB, SC. Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 96

Cho hình chóp S.ABCD. Gọi M, N, P lần lượt nằm trên các cạnh SA, SB, SC. Tìm giao điểm của (MNP) và SD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 97

Cho phân thức $A = \frac{4 x^{2} - 2 x + 7}{2 x - 1} (x \neq \frac{1}{2})$ . Tìm x Î ℤ để A Î ℤ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 98

Tìm phân thức P biết $P : \frac{4 x^{2} - 16}{2 x + 1} = \frac{4 x^{2} + 4 x + 1}{x - 2}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 99

Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC, điểm D thuộc AC sao cho $A D = \frac{a}{2}$ . Chứng minh rằng BD vuông góc với AM.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 100

Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Tính độ dài của $\vec{A B} + \vec{A C}$ và $\vec{A B} - \vec{A C}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 101

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho

$|2 (\vec{M A} + \vec{M B} + \vec{M C})| = |3 (\vec{M B} + \vec{M C})|$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 102

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn:

$|\vec{M A} + \vec{M C}| = |\vec{M A} - \vec{M B}|$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 103

Vẽ đồ thị hàm số $y = \frac{1}{2} x + 3 (d_{1})$ và $y = \frac{3}{2} x - 1 (d_{2})$ .

a) Tìm tọa độ giao điểm bằng phép toán.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 104

b) Xác định a, b để (d): y = ax + b song song với (d₂) và cắt (d₁) tại M(4; 5).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 105

Cho hai hàm số $y = \frac{1}{2} x (d_{1})$ và $y = 2 x - 3 (d_{2})$ .

a) Tìm tọa độ giao điểm của (d₁) và (d₂).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 106

b) Cho đường thẳng (d₃): y = ax + b. Tìm a và b biết (d₃) song song với (d₂) và (d₃) cắt (d₁) tại điểm có tung độ bằng −2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 107

Cho đường thẳng (d): y = (m + 2)x − m² (m là tham số). Tìm m để đường thẳng (d) và các đường thẳng y = x − 1; x − 2y = 3 cắt nhau tại một điểm.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 108

Cho (P): y = x² và đường thẳng (d): y = (m + 2)x − 2m (m là tham số).

a) Tìm m để đường thẳng (d) cắt (P) tại hai điểm phân biệt A và B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 109

b) Gọi hoành độ của A và B lần lượt là x₁, x₂. tìm m để x₁² + (m + 2)x₂ = 12.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 110

Chứng minh rằng: 13ⁿ − 1 chia hết cho 12.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 111

Chứng minh với mọi n Î ℕ*, ta có: 13ⁿ − 1 chia hết cho 6.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 112

Cho hình vẽ:

Chứng minh AD // BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 113

Cho hình thang ABCD (AB // CD). Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc đáy BC. Chứng minh AD + BC = DC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 114

Một người làm 50 sản phảm thì hết 8 giờ. Hỏi người đó làm 12 giờ thì được bau nhiêu sản phẩm?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 115

Cho phương trình x² − (m − 2)x + m − 5 = 0 (1) trong đó m là tham số. Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt x₁, x₂ với mọi giá trị của m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 116

Tìm m để các nghiệm x₁, x₂ của phương trình:

x² + (m − 2).x + m + 5 = 0 thỏa mãn x₁² + x₂² = 10.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 117

Cho hình lục giác đều ABCDEF tâm O. Chứng minh:

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} + \vec{O E} + \vec{O F} = \vec{0}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 118

Cho lục giác đều ABCDEF có tâm là O. Chứng minh rằng:

$\vec{O A} + \vec{O C} + \vec{O E} = \vec{0}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

4.6

12016 Đánh giá

50%

40%

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 23)

🔥 Đề thi HOT:

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

Danh sách câu hỏi:

Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q. a) Chứng minh rằng AP.AQ = AI2.

b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh rằng AK.AB = AP.AQ.

c) Chứng minh rằng K là trung điểm của AI.

Cho đường tròn (C) tâm O với I là trung điểm của dây AB không đi qua O. Một đường thẳng thay đổi đi qua A cắt đường tròn (C1) tâm O bán kính OI tại P và Q. Chứng minh rằng: a) Tích AP.AQ không đổi.

b) Đường tròn ngoại tiếp tam giác BPQ luôn đi qua một điểm cố định khác B.

Cho parabol P: y=12x2và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n. a) Tìm tọa độ hai điểm A, B. Tìm m, n biết (d) đi qua hai điểm A, B.

b) Tính độ dài đường cao OH của tam giác OAB. (điểm O là gốc tọa độ).

Cho parabol P: y=12x2 và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n. a) Tìm tọa độ hai điểm A, B.

b) Tìm m, n biết (d) đi qua hai điểm A, B.

Cho tan a + cot a = m. Tìm m để tan2 a + cot2 a = 7.

Cho tan a + cot a = m. Tính tan3 a + cot3 a theo m.

Cho biểu thức A=x+2x+3−5x2+x−6+12−x . a) Tìm điều kiện của x để A có nghĩa.

b) Rút gọn A.

c) Tìm x để A=−34 .

d) Tìm x để biểu thức A có giá trị nguyên

e) Tìm giá trị của A khi x2 − 9 = 0.

Cho biểu thức P=x+2x+3−5x2+x−6+12−x . Tìm x để P=−34 .

Tìm số có 3 chữ số, biết rằng nếu bỏ chữ số 0 ở tận cùng bên phải số đó ta được số mới mà hiệu của số mới và số đã cho bằng 135.

Tìm số tự nhiên có 3 chữ số biết rằng nếu viết thêm 1 chữ số 0 vào giữa chữ số hàng trăm và hàng chục của số đó ta được số mới gấp 6 lần số phải tìm.

Giải phương trình 9x2+x−1−10.3x2+x−2+1=0 .

Phương trình 9x2+x−1−10.3x2+x−2+1=0 có tập nghiệm là

Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.

Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh a = b = c.

Cho hình thoi ABCD, có A^=60° . Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh 5 điểm E, F, G, H, B, D cùng thuộc một đường tròn

Cho tam giác ABC vuông cân đỉnh A. Qua A kẻ đường thẳng d cắt BC. Vẽ BM, CN cùng vuông góc với d. Chứng minh: ∆BAM = ∆CAN.

Chứng minh rằng: b) MN = BM + CN.

Số nghiệm của phương trình cos 2x + 3sin x − 2 = 0 trên khoảng (0; 20π) là bao nhiêu?

Giải phương trình: cos 2x + 3sin x − 2 = 0.

Tính sin x, cos x, tan x, cot x biết .sinx+cosx=2

Cho sinx+cosx=23 . Hãy tính: A = sin x.cos x.

Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật biết rằng SA vuông góc (ABCD), SC hợp với đáy một góc 45° và AB = 3a, BC =4a. Tính thể tích khối chóp.

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc với mặt phẳng đáy, SC tạo với đáy một góc 45° và SC=2a2 . Thể tích khối chóp S.ABCD.

Cho đường tròn (O) tâm O đường kính AB lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn (O) tại điểm C cắt tia OI tại điểm D. a) Chứng minh OI // BC.

b) Chứng minh DA là tiếp tuyến đường tròn (O).

c) Vẽ CH vuông góc với AB, H thuộc AB và vẻ BK vuông góc với CD, K thuộc CD. Chứng minh: CK2 = AH.BH

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho AMB^=60° . Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho AMB^=60° . Biết chu vi tam giác MAB là 24 cm, tính độ dài bán kính đường tròn.

A \ B được gọi là phần bù của B trong A khi nào?

A−B≤A−B. Dấu “=” xảy ra khi nào?

a) Tìm BC của 4 và 6.

b) Tìm ƯC của 10 và 20.

Tìm ƯC thông qua tìm ƯCLN: 10; 20 và 70.

Cho biểu thức P=x−x+2x+1:xx+1−x−41−x . a) Rút gọn P.

b) Tìm giá trị của x để P < 0.

c) Tìm GTNN của P.

Cho biểu thức P=1+aa+1:1a−1−2aaa+a−a−1 . a) Rút gọn P.

b) Tìm giá trị của a để P < 1.

c) Tìm giá trị của P nếu .a=19−83

Trong mặt phẳng Oxy, cho A(2; 4), B(−1; 4), C(−5; 1). Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.

Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(−4; 2), B(2; 4), C(8; −2). Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Từ điểm P nằm ngoài đường tròn (O; R) vẽ 2 tiếp tuyến PA, PB tới (O) với A, B là các tiếp điểm. Vẽ AH vuông góc với đường kính BC. Chứng minh PC cắt AH tại trung điểm I của AH.

b) Chứng minh OB.AH = CH.PB và E là trung điểm của AH.

c) Giả sử PO = d. Tính AH theo R và d.

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn:MA→+MC→=MA→−MB→

Cho tam giác ABC. Tìm tập hợp các điểm M trong trường hợp sau:MA→=MB→

Cho phương trình x2 − (2m + 5)x + 2m + 1 = 0 với m là tham số có hai nghiệm dương phân biệt x1, x2. Tìm m thỏa mãn x1−x2 có giá trị nhỏ nhất.

Cho phương trình: x2 − 2(m − 1)x + 2m − 5 = 0 (1) a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biết với mọi m.

b) Tìm m để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 < 2 < x2.

Cho đường tròn (O) và dây cung AB của (O) không là đường kính. Gọi I là trung điểm của AB. Một đường thẳng thay đổi đi qua A cắt đường tròn tâm O bán kính OI tại P và Q.

a) Chứng minh rằng AP.AQ = AI².

b) Giả sử đường tròn ngoại tiếp tam giác BPQ cắt AB tại K khác B. Chứng minh

rằng AK.AB = AP.AQ.

Cho đường tròn (C) tâm O với I là trung điểm của dây AB không đi qua O. Một đường thẳng thay đổi đi qua A cắt đường tròn (C₁) tâm O bán kính OI tại P và Q. Chứng minh rằng:

a) Tích AP.AQ không đổi.

Cho parabol $(P) : y = \frac{1}{2} x^{2}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n.

a) Tìm tọa độ hai điểm A, B. Tìm m, n biết (d) đi qua hai điểm A, B.

Cho parabol $(P) : y = \frac{1}{2} x^{2}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là −1; 2. Đường thẳng (d) có phương trình y = mx + n.

a) Tìm tọa độ hai điểm A, B.

Cho tan a + cot a = m. Tìm m để tan² a + cot² a = 7.

Cho tan a + cot a = m. Tính tan³ a + cot³ a theo m.

Cho biểu thức $A = \frac{x + 2}{x + 3} - \frac{5}{x^{2} + x - 6} + \frac{1}{2 - x}$ .

a) Tìm điều kiện của x để A có nghĩa.

c) Tìm x để $A = \frac{- 3}{4}$ .

e) Tìm giá trị của A khi x² − 9 = 0.

Cho biểu thức $P = \frac{x + 2}{x + 3} - \frac{5}{x^{2} + x - 6} + \frac{1}{2 - x}$ . Tìm x để $P = \frac{- 3}{4}$ .

Giải phương trình $9^{x^{2} + x - 1} - {10.3}^{x^{2} + x - 2} + 1 = 0$ .

Phương trình $9^{x^{2} + x - 1} - {10.3}^{x^{2} + x - 2} + 1 = 0$ có tập nghiệm là

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Cho a² + b² + c² = ab + bc + ca. Chứng minh a = b = c.

Cho hình thoi ABCD, có $\hat{A} = 60 °$ . Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh 5 điểm E, F, G, H, B, D cùng thuộc một đường tròn

Chứng minh rằng:

b) MN = BM + CN.

Tính sin x, cos x, tan x, cot x biết . $\sin x + \cos x = \sqrt{2}$

Cho $\sin x + \cos x = \frac{2}{3}$ . Hãy tính: A = sin x.cos x.

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc với mặt phẳng đáy, SC tạo với đáy một góc 45° và $S C = 2 a \sqrt{2}$ . Thể tích khối chóp S.ABCD.

Cho đường tròn (O) tâm O đường kính AB lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn (O) tại điểm C cắt tia OI tại điểm D.

a) Chứng minh OI // BC.

c) Vẽ CH vuông góc với AB, H thuộc AB và vẻ BK vuông góc với CD, K thuộc CD. Chứng minh: CK² = AH.BH

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\hat{A M B} = 60 °$ . Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB

Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\hat{A M B} = 60 °$ . Biết chu vi tam giác MAB là 24 cm, tính độ dài bán kính đường tròn.

$|A| - |B| \leq |A - B|$ . Dấu “=” xảy ra khi nào?

Cho biểu thức $P = (\sqrt{x} - \frac{x + 2}{\sqrt{x} + 1}) : (\frac{\sqrt{x}}{\sqrt{x} + 1} - \frac{\sqrt{x} - 4}{1 - x})$ .

a) Rút gọn P.

Cho biểu thức $P = (1 + \frac{\sqrt{a}}{a + 1}) : (\frac{1}{\sqrt{a} - 1} - \frac{2 \sqrt{a}}{a \sqrt{a} + \sqrt{a} - a - 1})$ .

a) Rút gọn P.

c) Tìm giá trị của P nếu . $a = 19 - 8 \sqrt{3}$

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn: $|\vec{M A} + \vec{M C}| = |\vec{M A} - \vec{M B}|$

Cho tam giác ABC. Tìm tập hợp các điểm M trong trường hợp sau: $\vec{M A} = \vec{M B}$

Cho phương trình x²− (2m + 5)x + 2m + 1 = 0 với m là tham số có hai nghiệm dương phân biệt x₁, x₂. Tìm m thỏa mãn $|\sqrt{x_{1}} - \sqrt{x_{2}}|$ có giá trị nhỏ nhất.

Cho phương trình: x² − 2(m − 1)x + 2m − 5 = 0 (1)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biết với mọi m.

b) Tìm m để phương trình (1) có 2 nghiệm x₁, x₂ thỏa mãn x₁ < 2 < x₂.

Cho tam giác ABC. Tìm tập hợp điểm M:

. $|\vec{M A} + \vec{M B} + \vec{M C}| = |\vec{M A} + 2 \vec{M B}|$

Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). AC cắt đường tròn (O) tại D (D khác C).

a) Chứng minh: BD ^ AC và AB² = AD.AC.

c) Chứng minh $\hat{O C H} = \hat{O A C}$ .

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho

$|2 (\vec{M A} + \vec{M B} + \vec{M C})| = |3 (\vec{M B} + \vec{M C})|$ .

Cho ∆ABC cân tại A. Kẻ AH ^ BC (H Î BC).

a) Chứng minh HB = HC.

Cho tam giác ABC cân tại A, kẻ AH ⊥ BC. Chứng minh:

a) HB = HC.

Tìm điều kiện của x để biểu thức $\frac{3 x - 1}{x^{2} - 4}$ là phân thức.

Cho sáu chữ số: 2, 3, 5, 6, 7, 9.

a) Có bao nhiêu số có ba chữ số, các chữ số trong mỗi số đều khác nhau, được lập thành từ các chữ số trên?

Xác định parabol y = ax²+ bx + c, (a ≠ 0), biết rằng đỉnh của parabol đó có tung độ bằng −25, đồng thời parabol đó cắt trục hoành tại hai điểm A(−4; 0) và B(6; 0).

Xác định parabol (p): y = ax²+ bx + c, (a ≠ 0), biết (p) cắt trục tung tại điểm có tung độ bằng 1 và có giá trị nhỏ nhất bằng $\frac{3}{4}$ khi $x = \frac{1}{2}$ .

Cho hai đường thẳng

(d₁): y = ax + b (a ≠ 0);

(d₂): y = a'x + b' (a' ≠ 0);

(d₁) và (d₂) song song, cắt nhau, trùng nhau khi nào?

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $(d_{1}) : \{\begin{cases} x = 4 + 2 t \\ y = 1 - 5 t \end{cases}$ và (d₂): 2x − 5y − 14 = 0.

Khẳng định nào sau đây đúng?

Tìm số hạng thứ 8 trong khai triển (1 − 2x)¹².

Hệ số của số hạng thứ 8 trong khai triển nhị thức Niu-tơn (2 + 3x)¹⁴.

Cho hàm số y = (m − 1)x + 2 có đồ thị là đường thẳng (d).

a) Tìm m biết (d) đi qua điểm M(2; 1).

Cho hàm số y = (m + 1)x − 2 có đồ thị là đường thẳng (d).

a) Tìm m để đồ thị hàm số (d) cắt đồ thị hàm số y = x + 3 tại điểm tung độ là 2.

Cho phân thức $A = \frac{4 x^{2} - 2 x + 7}{2 x - 1} (x \neq \frac{1}{2})$ . Tìm x Î ℤ để A Î ℤ.

Tìm phân thức P biết $P : \frac{4 x^{2} - 16}{2 x + 1} = \frac{4 x^{2} + 4 x + 1}{x - 2}$

Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC, điểm D thuộc AC sao cho $A D = \frac{a}{2}$ . Chứng minh rằng BD vuông góc với AM.

Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Tính độ dài của $\vec{A B} + \vec{A C}$ và $\vec{A B} - \vec{A C}$ .

Cho tam giác ABC. Tìm tập hợp các điểm M sao cho

$|2 (\vec{M A} + \vec{M B} + \vec{M C})| = |3 (\vec{M B} + \vec{M C})|$ .

Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn:

$|\vec{M A} + \vec{M C}| = |\vec{M A} - \vec{M B}|$ .

Vẽ đồ thị hàm số $y = \frac{1}{2} x + 3 (d_{1})$ và $y = \frac{3}{2} x - 1 (d_{2})$ .

a) Tìm tọa độ giao điểm bằng phép toán.

b) Xác định a, b để (d): y = ax + b song song với (d₂) và cắt (d₁) tại M(4; 5).

Cho hai hàm số $y = \frac{1}{2} x (d_{1})$ và $y = 2 x - 3 (d_{2})$ .

a) Tìm tọa độ giao điểm của (d₁) và (d₂).

b) Cho đường thẳng (d₃): y = ax + b. Tìm a và b biết (d₃) song song với (d₂) và (d₃) cắt (d₁) tại điểm có tung độ bằng −2.

Cho đường thẳng (d): y = (m + 2)x − m² (m là tham số). Tìm m để đường thẳng (d) và các đường thẳng y = x − 1; x − 2y = 3 cắt nhau tại một điểm.

Cho (P): y = x² và đường thẳng (d): y = (m + 2)x − 2m (m là tham số).

a) Tìm m để đường thẳng (d) cắt (P) tại hai điểm phân biệt A và B.

b) Gọi hoành độ của A và B lần lượt là x₁, x₂. tìm m để x₁² + (m + 2)x₂ = 12.

Chứng minh rằng: 13ⁿ − 1 chia hết cho 12.

Chứng minh với mọi n Î ℕ*, ta có: 13ⁿ − 1 chia hết cho 6.

Cho hình vẽ:

Chứng minh AD // BC.

Cho phương trình x² − (m − 2)x + m − 5 = 0 (1) trong đó m là tham số. Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt x₁, x₂ với mọi giá trị của m.

Tìm m để các nghiệm x₁, x₂ của phương trình:

x² + (m − 2).x + m + 5 = 0 thỏa mãn x₁² + x₂² = 10.

Cho hình lục giác đều ABCDEF tâm O. Chứng minh:

$\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} + \vec{O E} + \vec{O F} = \vec{0}$ .

Cho lục giác đều ABCDEF có tâm là O. Chứng minh rằng:

$\vec{O A} + \vec{O C} + \vec{O E} = \vec{0}$ .