5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 19)

53 người thi tuần này 4.6 60.1 K lượt thi 78 câu hỏi 90 phút

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41
Đề số 42
Đề số 43
Đề số 44
Đề số 45
Đề số 46
Đề số 47
Đề số 48
Đề số 49
Đề số 50
Đề số 51
Đề số 52
Đề số 53
Đề số 54
Đề số 55
Đề số 56
Đề số 57
Đề số 58
Đề số 59
Đề số 60
Đề số 61
Đề số 62
Đề số 63
Đề số 64
Đề số 65
Đề số 66
Đề số 67
Đề số 68
Đề số 69
Đề số 70
Đề số 71
Đề số 72
Đề số 73
Đề số 74
Đề số 75
Đề số 76
Đề số 77
Đề số 78
Đề số 79
Đề số 80
Đề số 81
Đề số 82
Đề số 83
Đề số 84
Đề số 85

🔥 Đề thi HOT:

2867 người thi tuần này

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

62.5 K lượt thi 126 câu hỏi

2316 người thi tuần này

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

15.3 K lượt thi 35 câu hỏi

1379 người thi tuần này

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

14 K lượt thi 20 câu hỏi

1374 người thi tuần này

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

13.1 K lượt thi 20 câu hỏi

1337 người thi tuần này

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

13.4 K lượt thi 40 câu hỏi

1307 người thi tuần này

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

16 K lượt thi 35 câu hỏi

1287 người thi tuần này

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

20.5 K lượt thi 25 câu hỏi

1042 người thi tuần này

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

9.8 K lượt thi 15 câu hỏi

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

19317 lượt thi

8 đề

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

15177 lượt thi

8 đề

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

16437 lượt thi

7 đề

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

14828 lượt thi

7 đề

225 Bài tập Số phức ôn thi Đại học có lời giải

11231 lượt thi

8 đề

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

23358 lượt thi

10 đề

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

20815 lượt thi

9 đề

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

13053 lượt thi

8 đề

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

7556 lượt thi

7 đề

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

6233 lượt thi

3 đề

Danh sách câu hỏi:

Câu 1

Cho hàm số y = x + 4 (d).

a) Vẽ đồ thị của hàm số trên mặt phẳng tọa độ Oxy

b) Tính diện tích của ∆AOB (đơn vị đo trên các trục tọa độ là xen ti mét)

Xem đáp án

Lời giải

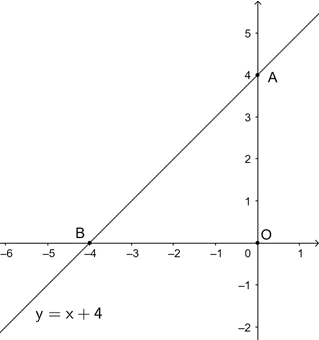
Media VietJack

a) y = x + 4 (d).

• Với x = 0 Þ y = 4;

• Với y = 0 Þ x = −4.

Vậy đồ thị hàm số (d): y = x + 4 đi qua hai điểm A(0; 4) và B(−4; 0).

b) Ta có OA = 4 và OB = 4.

Do đó, diện tích của ∆AOB là: \({S_{OAB}} = \frac{1}{2}.4.4 = 8\;\left( {c{m^2}} \right)\).

Câu 2

Cho hàm số bậc nhất y = (m − 1)x + 3 (1) (với m ≠ 1)
a) Xác định m để đồ thị hàm số (1) song song với đường thắng y = −x + 1
b) Xác định m để đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 và đồ thị hàm số (1) cùng đi qua một điểm.

Xem đáp án

Lời giải

a) Để đồ thị hàm số (1) song song với đường thắng y = −x + 1 thì
m − 1 = −1 Û m = 0.

b) Hoành độ giao điểm của đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 là nghiệm của phương trình:

1 − 3x = −0,5x − 1,5

Û 3x − 0,5x = 1 + 1,5

Û 2,5x = 2,5

Û x = 1

Với x = 1 Þ y = 1 − 3.1 = −2.

Vậy hai đường thẳng y =1 − 3x và y = −0,5x − 1,5 cắt nhau tại điểm M(1; −2).

Để đường thắng y =1 − 3x , đường thẳng y = −0,5x − 1,5 và đồ thị hàm số (1) cùng đi qua một điểm thì đồ thị hàm số (1) phải đi qua điểm M.

Suy ra −2 = (m − 1).1 + 3

Û −2 = (m − 1) + 3 Û m = −4.

Câu 3

Cho hàm số bậc nhất y = (m − 1)x + m − 3 (m ≠ 1) có đồ thị là đường thẳng d.

a) Khi m = 0, hãy vẽ đồ thị hàm số trên;

b) Tìm m để d cắt trục tung tại điểm có tung độ bằng 1;

c) Gọi A, B lần lượt là giao điểm của d với hai trục Ox, Oy. Tìm m để tam giác OAB cân.

Xem đáp án

Lời giải

a) Với m = 0 Þ y = − x − 3

Ta lập bảng:

x	0	−3
y	−3	0

Hàm số y = − x − 3 đi qua hai điểm M(0; −3) và N(−3; 0).

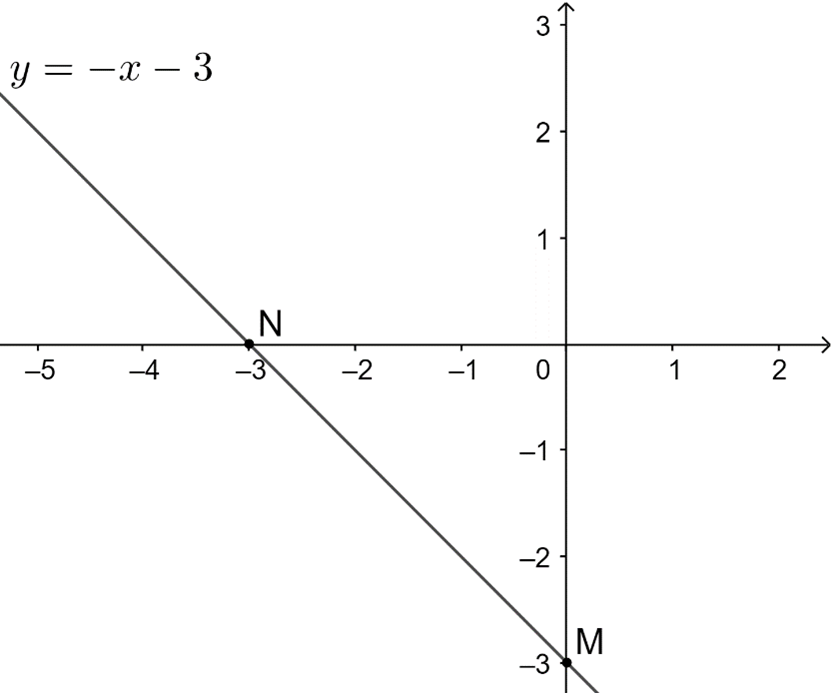
Media VietJack

b) (d) cắt trục tung tại điểm có tung độ bằng 1

Þ 1 = (m − 1).0 + m − 3

Û 1 = m − 3

Û m = 4.

Vậy m = 4 thì (d) cắt trục tung tại điểm có tung độ bằng 1.

c) Vì A là giao điểm của (d) với trục Ox nên y_A = 0.

Khi đó (m − 1)x_A + m − 3 = 0

\[ \Leftrightarrow {x_A} = - \frac{{m - 3}}{{m - 1}}\]

\( \Rightarrow OA = \left| { - \frac{{m - 3}}{{m - 1}}} \right|\;\left( {m \ne 1} \right)\)

B là giao điểm của (d) vưới trục Oy nên x_B = 0

Khi đó y_B = (m − 1).0 + m − 3 = m − 3

\[ \Rightarrow OB = \left| {m - 3} \right|\]

Để tam giác OAB cân tại O thì OA = OB

\[ \Leftrightarrow \left| { - \frac{{m - 3}}{{m - 1}}} \right| = \left| {m - 3} \right|\]

+) TH1:

\[ - \frac{{m - 3}}{{m - 1}} = m - 3\]

\( \Rightarrow \left( {m - 3} \right)\left( {m - 1} \right) = - \left( {m - 3} \right)\)

\[ \Leftrightarrow \left( {m - 3} \right)\left( {m - 1} \right) + \left( {m - 3} \right) = 0\]

Û m(m − 3) = 0

\[ \Rightarrow \left[ \begin{array}{l}m = 0\;\left( {TM} \right)\\m = 3\;\left( {TM} \right)\end{array} \right.\]

+) TH2:

\[ - \frac{{m - 3}}{{m - 1}} = - \left( {m - 3} \right)\]

\( \Rightarrow \left( {m - 3} \right)\left( {m - 1} \right) = \left( {m - 3} \right)\)

\[ \Leftrightarrow \left( {m - 3} \right)\left( {m - 1} \right) - \left( {m - 3} \right) = 0\]

Û (m − 2)(m − 3) = 0

\[ \Rightarrow \left[ \begin{array}{l}m = 2\;\left( {TM} \right)\\m = 3\;\left( {TM} \right)\end{array} \right.\]

Vậy các giá trị của m thỏa mãn là m = 1; m = 2; m = 3.

Câu 4

Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC (E khác B và C), AE cắt CD tại F. Chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn.

b) AE . AF = AC².

c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.

Xem đáp án

Lời giải

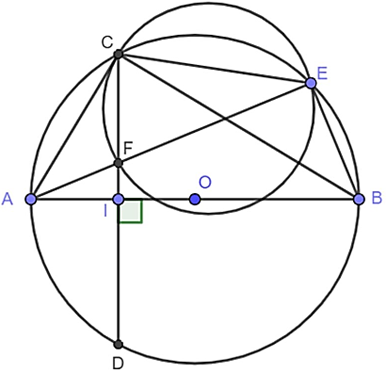
Media VietJack

a) Tứ giác BEFI có: \[\widehat {BIF} = 90^\circ \] (giả thiết)

Suy ra I thuộc đường tròn đường kính BF.

\[\widehat {BEF} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)

Nên E thuộc đường tròn đường kính BF

Þ BEFI nội tiếp đường tròn đường kính BF.

b) AB ^ CD

• Xét ∆OCD cân có OI là đường cao nên cũng là đường trung tuyến, nên I là trung điểm của CD.

• Xét ∆ACD có AI vừa là đường cao vừa là đường trung tuyến nên ∆ACD cân tại đỉnh A nên AC = AD

Þ \(\widehat {ACF} = \widehat {AEC}\) (hai góc nội tiếp chắn hai cung bằng nhau)

Xét ∆ACF và ∆AEC có:

\(\widehat A\) chung

\(\widehat {ACF} = \widehat {AEC}\) (cmt)

Þ ∆ACF ᔕ ∆AEC (g.g)

\[ \Rightarrow \frac{{AC}}{{AE}} = \frac{{AF}}{{AC}}\] (hai cạnh tương ứng tỉ lệ)

Þ AE . AF = AC²

c) \(\widehat {ACF} = \widehat {AEC}\) Þ AC là tiếp tuyến đường tròn ngoại tiếp ∆CEF (1)

Mặt khác \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Þ AC ^ CB (2)

Từ (1) và (2) suy ra CB chứa đường kính đường tròn ngoại tiếp ∆CEF

Mà CB cố định nên tâm đường tròn ngoại tiếp ∆CEF thuộc CB cố định khi E thay đổi trên cung nhỏ BC.

Câu 5

Cho đường tròn (O) bán kính R, đường kính AB, vẽ dây cung CD vuông góc với AB (CD không đi qua (O)), trên tia đối của BA lấy S, SC cắt đường tròn tại M thuộc cung nhỏ BC

a) Chứng minh ∆SMA ᔕ ∆SBC.

b) Gọi H là giao điểm của MA và BC, K là giao điểm của MD và AB. Chứng minh tứ giác BMHK nội tiếp và HK // CD.

c) Chứng minh OK . OS = R².

Xem đáp án

Lời giải

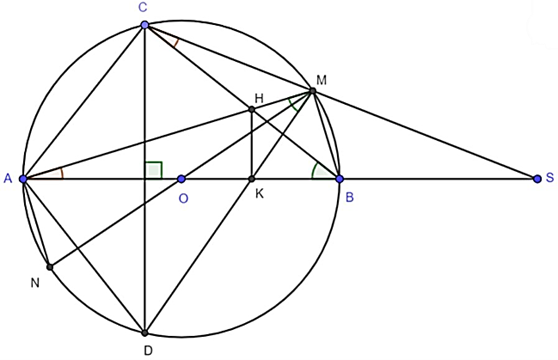
Media VietJack

a) Xét ∆SMA và ∆SBC có:

\[\widehat S\] chung

\(\widehat {SAM} = \widehat {SCB}\) (Hai góc nội tiếp cùng chắn cung MB của (O))

Þ ∆SMA ᔕ ∆SBC (g.g)

b) Do CD ^ AB (giả thiết)

Þ AB là đường trung trực của CD (mối liên hệ giữa đường kính và dây cung)

Þ AC = AD (tính chất đường trung trực)

(hai dây bằng nhau căng hai cung bằng nhau)

\( \Rightarrow \widehat {AMD} = \widehat {ABC}\) (góc nội tiếp cùng chắn hai cung bằng nhau)

\( \Rightarrow \widehat {KBH} = \widehat {KMH}\).

Mà hai góc này cùng nhìn cạnh KH nên suy ra BMHK nội tiếp.

c) Kẻ đường kính MN

Xét ∆AON và ∆BOM có:

OA = OB = R

\(\widehat {AON} = \widehat {BOM}\)

ON = OM = R

Þ ∆AON = ∆BOM (c.g.c)

Þ AN = BM (hai cạnh tương ứng bằng nhau)

(hai dây bằng nhau căng hai cung bằng nhau)

Ta có:

(tính chất góc có đỉnh nằm ngoài đường tròn) (1)

(tính chất góc nội tiếp)

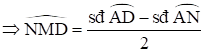Media VietJack (2)

Mà (3)

(4)

Từ (1), (2), (3) và (4) suy ra \(\widehat {ASC} = \widehat {NMD}\) hay \[\widehat {OMK} = \widehat {OSM}\]

Xét ∆OKM và ∆OMS có:

\(\widehat {MOS}\) chung

\[\widehat {OMK} = \widehat {OSM}\] (cmt)

Þ ∆OKM ᔕ ∆OMS (g.g)

\( \Rightarrow \frac{{OK}}{{OM}} = \frac{{OM}}{{OS}}\) (hai cạnh tương ứng tỉ lệ)

Þ OK.OS = OM² = R².

Câu 6

Số đo các góc của một đa giác lồi có 9 cạnh lập thành một cấp số cộng có công sai d = 3°. Tìm số đo của các góc đó

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tổng số đo các góc của đa giác đều 9 cạnh là:

A. 900°;

B. 1026°;

C. 1080°;

D. 1260°.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Viết phương trình đường thẳng đi qua 2 điểm A(1; 2) và B(3; 4).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Viết phương trình đường thẳng đi qua 2 điểm A(−1; −2) và B(3; −10)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Xác định hàm số bậc hai thỏa mãn điều kiện.

a) Cho (P): y = ax² + bx + c. Tìm a, b, c biết (P) đi qua điểm A(1; 2) và có đỉnh I(−1; −2).

b) Tìm hàm số y = ax² + bx − 3 biết đồ thị có tọa độ đỉnh là \(I\left( {\frac{1}{2};\; - 5} \right)\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Tìm m để đồ thị hàm số y = x² − mx + 1 đi qua điểm M(1; 2)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

Hàm số f (2x − 2) − 2e^x nghịch biến trên khoảng nào dưới đây?

A. (0; 1);

B. (1; +∞);

C. (−∞; −1);

D. (−2; 0).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Giải phương trình:

\(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Phương trình \(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\) có hai nghiệm là x₁, x₂. Tích x₁x₂ bằng:

A. \( - \frac{{27}}{2}\);

B. \(\frac{{27}}{2}\);

C. −42;

D. 42.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hàm số y = 3x − 2

a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên.

b) Tìm m để đường thẳng y = 3x − 2 cắt đường thẳng y = mx + 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho hàm số y = 3x – 2.

a) Vẽ đồ thị (d) của hàm số.

b) Tìm phương trình đường thẳng song song với (d) cắt trục hoành tại điểm có hoành độ bằng 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.
a) Tính BC, BH, HC, AH .

b) Kẻ phân giác AD. Tính BD, DC.
c) Tính diên tích tam giác AHD.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Cho ∆ABC vuông tại A vẽ đường cao AH có AB = 6 cm, AC = 8 cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính BC, AH, HC.

c) Chứng minh AH² = HB . HC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

a) Tìm hệ số của x¹²y¹³ trong khai triển (x + y)²⁵.

b) Tìm hệ số của x¹²y¹³ trong khai triển (x − y)²⁵.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Tìm hệ số của x¹²y¹³ trong khai triển (2x + 3y)²⁵.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x) = x²[f (x − 1)]⁴ là:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x) = x⁴[f (x − 1)]² là:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Cho hàm số: y = x³ − 3mx² + 9x + 1, có đồ thị (Cm), với m là tham số. Tìm giá trị của tham số m để đường thẳng (dm): y = x + 10 − 3m cắt đồ thị (Cm) tại 3 điểm phân biệt A, B, C. Gọi k₁, k₂, k₃ là hệ số góc tiếp tuyến của (Cm) lần lượt tại A, B, C. Tìm giá trị của m để k₁ + k₂ + k₃ > 15.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1 (Cm).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Tìm điều kiện của tham số m để hàm số là hàm số bậc nhất:

a) \(y = \sqrt {5 - m} \left( {x - 1} \right)\);

b) \(y = \frac{{m + 1}}{{m - 1}}x + 3,5\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Cho hàm số: y = (m − 5)x + 1 (m là tham số).

a) Tìm m để hàm số trên là hàm số bậc nhất

b) Với giá trị nào của m thì hàm số trên đồng biến; nghịch biến trên ℝ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho tam giác ABC đều tâm O. M là điểm tùy ý trong tam giác. MD, ME, MF tương ứng vuông góc với BC, CA, AB. Chọn khẳng định đúng?

A. \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\overrightarrow {MO} \);

B. \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = 2\overrightarrow {MO} \);

C. \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \);

D. \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = 3\overrightarrow {MO} \).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Tìm số hạng thứ năm trong khai triển \({\left( {x + \frac{2}{x}} \right)^{10}}\) mà trong khai triển đó số mũ của x giảm dần.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của (1 + 2x)¹⁰ là?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Cho ∆ABC vuông tại A, AB < AC, đường cao AH. Gọi I là trung điểm của AB. Lấy điểm K đối xứng với B qua H, qua A dựng đường thẳng song song với BC cắt HI tại D
a) Tứ giác AKHD là hình gì? Chứng minh?
b) CM tứ giác AHBD là hình chữ nhật. Từ đó tính diện tích tứ giác AHBD nếu AH = 6 cm, AB = 10 cm

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Tập nghiệm của phương trình \(\log \left( {{x^2} - x - 6} \right) + x = \log \left( {x + 2} \right) + 4\) là

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - 6x + 7} \right) = {\log _2}\left( {x - 3} \right)\) là

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

cho hai đường thẳng: y = x + 3 (d₁), y = 3x + 7 (d₂).
a) Vẽ đồ thị của các hàm số đã cho trên cùng một hệ trục tọa độ Oxy.
b) Gọi giao điểm của đường thẳng (d₁) và (d₂) với trục Oy lần lượt là A và B. Tìm tọa độ trung điểm I của đoạn AB.
c) Gọi J là giao điểm của hai đường thẳng (d₁) và (d₂). Chứng minh tam giác OIJ là tam giác vuông. Tính diện tích của tam giác đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Cho 2 đường thẳng: \(\left( {{d_1}} \right):\;y = \frac{1}{2}x + 2\) và (d₂): y = −x + 2.

Gọi A, B lần lượt là giao điểm của (d₁) và (d₂) với trục Ox, C là giao điểm của (d₁), (d₂). Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho hàm số bậc nhất y = (m − 1)x + 4 (d).
a) Vẽ đồ thị khi m = 2.
b) Tìm m để (d) song song với đồ thị hàm số y = −3x + 2 (d₁).
c) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d₂) tại 1 điểm nằm bên trái trục tung.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho hàm số bậc nhất y = (m − 1)x + 4 có đồ thị là đường thẳng (d) (m là tham số và m ≠ 1).

a) Vẽ đồ thị khi m = 2.

b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y = −3x + 2 (d₁).

c) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại hai điểm A, B sao cho diện tích tam giác OAB bằng 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Cho đường tròn (O; R) và một điểm A sao cho OA = 2R, vẽ các tiếp tuyến AB, AC với (O; R), B và C là các tiếp điểm. Vẽ đường kính BOD.

a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.

b) Chứng minh rằng: DC // OA.

c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh rằng OCEA là hình thang cân.

d) Gọi I là giao điểm của đoạn OA và (O), K là giao điểm của tia SI và AB. Tính theo R diện tích tứ giác AKOS.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Giải phương trình nghiệm nguyên 12x² + 6xy + 3y² = 28(x + y)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Cho \(\widehat {uOz} = 30^\circ \) và tia Ou là tia đối của tia Ov. Khi đó hai góc \(\widehat {uOz};\;\,\,\widehat {vOz}\) được gọi là hai góc gì? Và góc \(\widehat {vOz}\) bằng bao nhiêu độ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Cho a² + b² + c² = ab + bc + ca. Chứng minh a = b = c

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Cho phương trình x² − 2(m + 3)x + m² − 1 = 0.

Tìm m để Q = x₁ + x₂ − 3x₁x₂ có giá trị lớn nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Cho phương trình: x² − mx + m − 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x₁ và x₂ thoả mãn: x₁² + 3x₁x₂ = 3x₂ + 3m + 16.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Tìm giá trị nhỏ nhất của biểu thức sau: A = 4x² + 4x + 11.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Giải phương trình nghiệm nguyên: x² + 2xy = 5y + 6.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Giải phương trình nghiệm nguyên: x² − 2xy + 5y² = y + 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 51

Cho \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0\). Tính giá trị biểu thức \(P = \frac{{ab}}{{{c^2}}} + \frac{{bc}}{{{a^2}}} + \frac{{ac}}{{{b^2}}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 52

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 53

Chứng minh a² + b² + c² < 2(ab + bc + ca) với mọi số thực a, b, c là độ dài ba cạnh của một tam giác.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 54

Chứng minh \(\frac{{{a^3}}}{b} + \frac{{{b^3}}}{c} + \frac{{{c^3}}}{a} \ge ab + bc + ca\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 55

Cho a, b, c > 0 thỏa a² + b² + c² = 3. CMR:

\(\frac{{{a^3}{b^3}}}{c} + \frac{{{b^3}{c^3}}}{a} + \frac{{{a^3}{c^3}}}{b} \ge 3abc\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 56

Tìm x, y, z thuộc ℤ thỏa mãn: 3x² + 6y² + z² + 3y².z² − 18x = 6.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 57

Tìm tất cả các số nguyên x, y, z thỏa mãn:

3x² + 6y² + 2z² + 3y²z² − 18 = 6

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 58

Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc \(\widehat {BAC}\) = 30°. Tính diện tích tam giác ABC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 59

Cho ΔABC có AB = 4, AC = 6, \(\cos \widehat B = \frac{1}{8}\) và \(\cos \widehat C = \frac{3}{4}\). Tính cạnh BC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 60

Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Tính \(\cos \left( {\widehat B + \widehat C} \right)\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 61

Phương trình \({x^3} - 12x + m - 2 = 0\) có 3 nghiệm phân biệt với m:

A. −16 < m < 16;

B. −18 < m < 14;

C. −14 < m < 18;

D. −4 < m < 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 62

Tìm m để phương trình sau có 3 nghiệm phân biệt.

x³ − 6x² + 3(m + 2)x − m − 6 = 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 63

Cho điểm A nằm ngoài đường tròn (O; R). Vẽ 2 tiếp tuyến AB, AC với đường tròn (O), (B, C là các tiếp điểm). Vẽ đường kính CD của đường tròn (O).

a) Chứng minh rằng: OA ^ BC và OA // BD.

b) Gọi E là giao điểm của AD và đường tròn (O) (E khác D), H là giao điểm của OA và BC. Chứng minh rằng: AE.AD = AH.AO.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 64

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD // AO.

c) Tính độ dài các cạnh của tam giác ABC, biết OB = 2 cm; OA = 4 cm.

d) Đường thẳng AD cắt đường tròn (O) tại điểm thứ hai là M.

Chứng minh: AM.AD = AH.AO.

e) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại E. Chứng minh ED là tiếp tuyến của đường tròn (O).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 65

Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.

a) Tính các góc của hình thang cân.

b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 66

Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, \(\widehat {BAC} = \widehat {CAD}\). Tính AD nếu chu vi của hình thang bằng 20 cm và góc \(\widehat D = 60^\circ \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 67

Chứng minh rằng x²⁰⁰² + x²⁰⁰⁰ + 1 chia hết cho x² + x + 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 68

Tìm x để x² + x + 1 chia hết cho x – 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 69

Cho (O; R), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh: ∆OBA vuông tại B và ∆OAK cân tại K.
b) Đường thẳng KI cắt AB tại M. Chứng minh rằng KM là tiếp tuyến của đường tròn (O).
c) Tính chu vi tam giác AMK theo R.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 70

Cho đường tròn (O; R) và điểm A cách O một khoảng 2R. Từ A vẽ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Đường thảng vuông góc với B tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M.

a) Chứng minh: AMON là hình thoi.

b) Chứng minh: MN là tiếp tuyến của đường tròn.

c) Tính diện tích AMON.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 71

Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho \(AM = \frac{1}{5}AB\). Tìm k trong \(\overrightarrow {MA} = k\overrightarrow {MB} \).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 72

Cho nửa đường tròn (O), đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K, B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP // KM. Gọi Q là giao điểm của các đường thẳng AP và BM; E là giao điểm của PB và AM.

a) Chứng minh rằng tứ giác PQME nội tiếp đường tròn.

b) Chứng minh: ∆AKN = ∆BKM.

c) Chứng minh: AM . BE = AN . AQ.

d) Gọi R, S lần lượt là giao điểm thứ hai của QA, QB với đường tròn ngoại tiếp ∆OMP. Chứng minh rằng khi M di động trên cung KB thì trung điểm I của RS luôn nằm trên một đường cố định

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 73

Cho nửa đường tròn (O) đường kính AB và K là điểm chính giữa cung AB. Trên cung KB lấy một điểm M (khác K; B). Trên tia AM lấy điểm N sao cho AN = BM. Kẻ dây BP song song với KM. Gọi Q là giao điểm của các đường thẳng AP, BM.

a) So sánh hai tam giác: ΔAKN và ΔBKM.

b) Chứng minh: ΔKMN vuông cân.

c) Tứ giác ANKP là hình gì? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 74

Cho tam giác ABC có \(\widehat A = {90^^\circ }\), AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh rằng AK = AD

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 75

Cho tam giác ABC đều cạnh a và AM là trung tuyến của tam giác. Tính tích vô hướng sau: \(\overrightarrow {AC} \left( {2\overrightarrow {AB} - 3\overrightarrow {AC} } \right)\)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 76

Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng \(\overrightarrow {AB} \,.\,\overrightarrow {BC} \)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 77

Gieo một con xúc xắc cân đối đồng chất hai lần. Tính xác suất để biến cố có tổng hai mặt bằng 8.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 78

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 8.

b) Tích số chấm hai mặt xuất hiện là số lẻ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

4.6

12016 Đánh giá

50%

40%

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 19)

🔥 Đề thi HOT:

5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)

135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)

80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)

80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)

148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)

140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)

238 câu Bài tâp Nguyên Hàm, Tích phân cơ bản, nâng cao cực hay có lời giải (P1)

15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)

Nội dung liên quan:

237 câu Bài tập Hàm số mũ, logarit ôn thi Đại học có lời giải

240 câu Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải

215 câu Bài tập Hàm số mũ, logarit cơ bản, nâng cao có lời giải

175 câu Bài tập Số phức cơ bản, nâng cao có lời giải

225 Bài tập Số phức ôn thi Đại học có lời giải

250 câu Bài tập Tích phân ôn thi Đại học có lời giải

213 câu Bài tập Tích phân cơ bản, nâng cao có lời giải

299 Bài trắc nghiệm hàm số mũ, hàm số Logarit siêu hay có lời giải chi tiết

255 Bài trắc nghiệm Hàm số mũ và Logarit cơ bản nâng cao cực hay có lời giải

71 Bài trắc nghiệm Khối đa diện trong đề thi Đại học cực hay có lời giải

Danh sách câu hỏi:

Cho hàm số y = x + 4 (d). a) Vẽ đồ thị của hàm số trên mặt phẳng tọa độ Oxy b) Tính diện tích của ∆AOB (đơn vị đo trên các trục tọa độ là xen ti mét)

Số đo các góc của một đa giác lồi có 9 cạnh lập thành một cấp số cộng có công sai d = 3°. Tìm số đo của các góc đó

Tổng số đo các góc của đa giác đều 9 cạnh là:

Viết phương trình đường thẳng đi qua 2 điểm A(1; 2) và B(3; 4).

Viết phương trình đường thẳng đi qua 2 điểm A(−1; −2) và B(3; −10)

Xác định hàm số bậc hai thỏa mãn điều kiện.

Tìm m để đồ thị hàm số y = x2 − mx + 1 đi qua điểm M(1; 2)

Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau Hàm số f (2x − 2) − 2ex nghịch biến trên khoảng nào dưới đây?

Giải phương trình: \(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\)

Phương trình \(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\) có hai nghiệm là x1, x2. Tích x1x2 bằng:

Cho hàm số y = 3x − 2 a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên. b) Tìm m để đường thẳng y = 3x − 2 cắt đường thẳng y = mx + 2.

Cho hàm số y = 3x – 2. a) Vẽ đồ thị (d) của hàm số. b) Tìm phương trình đường thẳng song song với (d) cắt trục hoành tại điểm có hoành độ bằng 2.

Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.a) Tính BC, BH, HC, AH . b) Kẻ phân giác AD. Tính BD, DC.c) Tính diên tích tam giác AHD.

Cho ∆ABC vuông tại A vẽ đường cao AH có AB = 6 cm, AC = 8 cm. a) Chứng minh ∆HBA ᔕ ∆ABC. b) Tính BC, AH, HC. c) Chứng minh AH2 = HB . HC.

a) Tìm hệ số của x12y13 trong khai triển (x + y)25. b) Tìm hệ số của x12y13 trong khai triển (x − y)25.

Tìm hệ số của x12y13 trong khai triển (2x + 3y)25.

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: Số điểm cực trị của hàm số g(x) = x2[f (x − 1)]4 là:

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: Số điểm cực trị của hàm số g(x) = x4[f (x − 1)]2 là:

Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x3 − 3mx2 − 9x + 1 (Cm).

Tìm điều kiện của tham số m để hàm số là hàm số bậc nhất: a) \(y = \sqrt {5 - m} \left( {x - 1} \right)\); b) \(y = \frac{{m + 1}}{{m - 1}}x + 3,5\).

Cho hàm số: y = (m − 5)x + 1 (m là tham số). a) Tìm m để hàm số trên là hàm số bậc nhất b) Với giá trị nào của m thì hàm số trên đồng biến; nghịch biến trên ℝ?

Cho tam giác ABC đều tâm O. M là điểm tùy ý trong tam giác. MD, ME, MF tương ứng vuông góc với BC, CA, AB. Chọn khẳng định đúng?

Tìm số hạng thứ năm trong khai triển \({\left( {x + \frac{2}{x}} \right)^{10}}\) mà trong khai triển đó số mũ của x giảm dần.

Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của (1 + 2x)10 là?

Tập nghiệm của phương trình \(\log \left( {{x^2} - x - 6} \right) + x = \log \left( {x + 2} \right) + 4\) là

Tập nghiệm của phương trình \({\log _2}\left( {{x^2} - 6x + 7} \right) = {\log _2}\left( {x - 3} \right)\) là

Cho hàm số bậc nhất y = (m − 1)x + 4 (d).a) Vẽ đồ thị khi m = 2.b) Tìm m để (d) song song với đồ thị hàm số y = −3x + 2 (d1).c) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d2) tại 1 điểm nằm bên trái trục tung.

Giải phương trình nghiệm nguyên 12x2 + 6xy + 3y2 = 28(x + y)

Cho \(\widehat {uOz} = 30^\circ \) và tia Ou là tia đối của tia Ov. Khi đó hai góc \(\widehat {uOz};\;\,\,\widehat {vOz}\) được gọi là hai góc gì? Và góc \(\widehat {vOz}\) bằng bao nhiêu độ?

Viết tên các cặp góc phụ nhau, bù nhau có trong hình sau:

Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh a = b = c

Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.

Cho phương trình x2 − 2(m + 3)x + m2 − 1 = 0. Tìm m để Q = x1 + x2 − 3x1x2 có giá trị lớn nhất.

Cho phương trình: x2 − mx + m − 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x1 và x2 thoả mãn: x12 + 3x1x2 = 3x2 + 3m + 16.

Tìm giá trị nhỏ nhất của biểu thức sau: A = 4x2 + 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x2 − 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x2 − 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x2 − 4x + 11.

Giải phương trình nghiệm nguyên: x2 + 2xy = 5y + 6.

Giải phương trình nghiệm nguyên: x2 − 2xy + 5y2 = y + 1.

Cho \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 0\). Tính giá trị biểu thức \(P = \frac{{ab}}{{{c^2}}} + \frac{{bc}}{{{a^2}}} + \frac{{ac}}{{{b^2}}}\).

Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca.

Chứng minh a2 + b2 + c2 < 2(ab + bc + ca) với mọi số thực a, b, c là độ dài ba cạnh của một tam giác.

Chứng minh \(\frac{{{a^3}}}{b} + \frac{{{b^3}}}{c} + \frac{{{c^3}}}{a} \ge ab + bc + ca\).

Cho a, b, c > 0 thỏa a2 + b2 + c2 = 3. CMR: \(\frac{{{a^3}{b^3}}}{c} + \frac{{{b^3}{c^3}}}{a} + \frac{{{a^3}{c^3}}}{b} \ge 3abc\).

Tìm x, y, z thuộc ℤ thỏa mãn: 3x2 + 6y2 + z2 + 3y2.z2 − 18x = 6.

Tìm tất cả các số nguyên x, y, z thỏa mãn: 3x2 + 6y2 + 2z2 + 3y2z2 − 18 = 6

Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc \(\widehat {BAC}\) = 30°. Tính diện tích tam giác ABC.

Cho ΔABC có AB = 4, AC = 6, \(\cos \widehat B = \frac{1}{8}\) và \(\cos \widehat C = \frac{3}{4}\). Tính cạnh BC.

Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Tính \(\cos \left( {\widehat B + \widehat C} \right)\).

Phương trình \({x^3} - 12x + m - 2 = 0\) có 3 nghiệm phân biệt với m:

Tìm m để phương trình sau có 3 nghiệm phân biệt. x3 − 6x2 + 3(m + 2)x − m − 6 = 0.

Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD. a) Tính các góc của hình thang cân. b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.

Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, \(\widehat {BAC} = \widehat {CAD}\). Tính AD nếu chu vi của hình thang bằng 20 cm và góc \(\widehat D = 60^\circ \).

Chứng minh rằng x2002 + x2000 + 1 chia hết cho x2 + x + 1.

Tìm x để x2 + x + 1 chia hết cho x – 1.

Cho đoạn thẳng AB và M là điểm nằm trên đoạn AB sao cho \(AM = \frac{1}{5}AB\). Tìm k trong \(\overrightarrow {MA} = k\overrightarrow {MB} \).

Cho tam giác ABC có \(\widehat A = {90^^\circ }\), AB = AC, điểm D thuộc cạnh AB. Đường thẳng qua B và vuông góc với CD cắt đường thẳng CA ở K. Chứng minh rằng AK = AD

Cho hàm số y = x + 4 (d).

a) Vẽ đồ thị của hàm số trên mặt phẳng tọa độ Oxy

b) Tính diện tích của ∆AOB (đơn vị đo trên các trục tọa độ là xen ti mét)

Xác định hàm số bậc hai thỏa mãn điều kiện.

a) Cho (P): y = ax² + bx + c. Tìm a, b, c biết (P) đi qua điểm A(1; 2) và có đỉnh I(−1; −2).

b) Tìm hàm số y = ax² + bx − 3 biết đồ thị có tọa độ đỉnh là \(I\left( {\frac{1}{2};\; - 5} \right)\).

Tìm m để đồ thị hàm số y = x² − mx + 1 đi qua điểm M(1; 2)

Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau

Hàm số f (2x − 2) − 2e^x nghịch biến trên khoảng nào dưới đây?

Giải phương trình:

\(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\)

Phương trình \(2{x^2} + 3x + \sqrt {2{x^2} + 3x + 9} = 33\) có hai nghiệm là x₁, x₂. Tích x₁x₂ bằng:

Cho hàm số y = 3x − 2

a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên.

b) Tìm m để đường thẳng y = 3x − 2 cắt đường thẳng y = mx + 2.

Cho hàm số y = 3x – 2.

a) Vẽ đồ thị (d) của hàm số.

b) Tìm phương trình đường thẳng song song với (d) cắt trục hoành tại điểm có hoành độ bằng 2.

Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.
a) Tính BC, BH, HC, AH .

b) Kẻ phân giác AD. Tính BD, DC.
c) Tính diên tích tam giác AHD.

Cho ∆ABC vuông tại A vẽ đường cao AH có AB = 6 cm, AC = 8 cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính BC, AH, HC.

c) Chứng minh AH² = HB . HC.

a) Tìm hệ số của x¹²y¹³ trong khai triển (x + y)²⁵.

b) Tìm hệ số của x¹²y¹³ trong khai triển (x − y)²⁵.

Tìm hệ số của x¹²y¹³ trong khai triển (2x + 3y)²⁵.

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x) = x²[f (x − 1)]⁴ là:

Cho hàm số bậc bốn f (x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số g(x) = x⁴[f (x − 1)]² là:

Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1 (Cm).

Tìm điều kiện của tham số m để hàm số là hàm số bậc nhất:

a) \(y = \sqrt {5 - m} \left( {x - 1} \right)\);

b) \(y = \frac{{m + 1}}{{m - 1}}x + 3,5\).

Cho hàm số: y = (m − 5)x + 1 (m là tham số).

a) Tìm m để hàm số trên là hàm số bậc nhất

b) Với giá trị nào của m thì hàm số trên đồng biến; nghịch biến trên ℝ?

Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của (1 + 2x)¹⁰ là?

Cho hàm số bậc nhất y = (m − 1)x + 4 (d).
a) Vẽ đồ thị khi m = 2.
b) Tìm m để (d) song song với đồ thị hàm số y = −3x + 2 (d₁).
c) Tìm m để (d) cắt đồ thị hàm số y = x − 7 (d₂) tại 1 điểm nằm bên trái trục tung.

Giải phương trình nghiệm nguyên 12x² + 6xy + 3y² = 28(x + y)

Cho a² + b² + c² = ab + bc + ca. Chứng minh a = b = c

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Cho phương trình x² − 2(m + 3)x + m² − 1 = 0.

Tìm m để Q = x₁ + x₂ − 3x₁x₂ có giá trị lớn nhất.

Cho phương trình: x² − mx + m − 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x₁ và x₂ thoả mãn: x₁² + 3x₁x₂ = 3x₂ + 3m + 16.

Tìm giá trị nhỏ nhất của biểu thức sau: A = 4x² + 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Tìm giá trị nhỏ nhất của A = 4x² − 4x + 11.

Giải phương trình nghiệm nguyên: x² + 2xy = 5y + 6.

Giải phương trình nghiệm nguyên: x² − 2xy + 5y² = y + 1.

Chứng minh bất đẳng thức: a² + b² + c² ≥ ab + bc + ca.

Chứng minh a² + b² + c² < 2(ab + bc + ca) với mọi số thực a, b, c là độ dài ba cạnh của một tam giác.

Cho a, b, c > 0 thỏa a² + b² + c² = 3. CMR:

\(\frac{{{a^3}{b^3}}}{c} + \frac{{{b^3}{c^3}}}{a} + \frac{{{a^3}{c^3}}}{b} \ge 3abc\).

Tìm x, y, z thuộc ℤ thỏa mãn: 3x² + 6y² + z² + 3y².z² − 18x = 6.

Tìm tất cả các số nguyên x, y, z thỏa mãn:

3x² + 6y² + 2z² + 3y²z² − 18 = 6

Tìm m để phương trình sau có 3 nghiệm phân biệt.

x³ − 6x² + 3(m + 2)x − m − 6 = 0.

Cho hình thang cân ABCD. Đáy nhỏ AB bằng cạnh bên BC và đường chéo AC vuông góc với cạnh bên AD.

a) Tính các góc của hình thang cân.

b) Chứng minh rằng trong hình thang cân đó đáy lớn gấp đôi đáy nhỏ.

Chứng minh rằng x²⁰⁰² + x²⁰⁰⁰ + 1 chia hết cho x² + x + 1.

Tìm x để x² + x + 1 chia hết cho x – 1.

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:

a) Tổng số chấm hai mặt xuất hiện bằng 8.

b) Tích số chấm hai mặt xuất hiện là số lẻ.