5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 79)
35 người thi tuần này 4.6 106 K lượt thi 81 câu hỏi 60 phút
- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
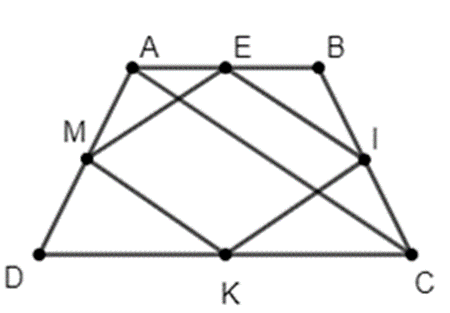
a) Xét ∆AED và ∆BEC có:
AE = BE
\(\widehat {EAD} = \widehat {EBC}\) (Vì ABCD là hình thang cân)
AD = BC (Vì ABCD là hình thang cân)
Do đó ∆AED = ∆BEC (c.g.c)
Þ ED = EC (Hai cạnh tương ứng bằng nhau)
Xét ∆EDC có DE = EC (cmt)
Do đó ∆EDC cân tại E
b) Xét ∆ADC có:
AM = MD (gt)
DK = KC (gt)
Do đó MK là đường trung bình của ∆ADC
Þ MK // AC và \(MK = \frac{1}{2}AC\) (1)
Chứng minh tương tự, ta có: EI là đường trung bình của ∆ABC
Þ EI // AC và \(EI = \frac{1}{2}AC\) (2)
Từ (1) và (2) suy ra: MK // EI và MK = EI
Do đó EIKM là hình bình hành (3)
Lại có: ME là đường trung bình của ∆ABD
\( \Rightarrow ME = \frac{1}{2}BD\)
Mà BD = AC (Vì ABCD là hình thang cân)
nên ME = MK (4)
Từ (3) và (4) suy ra: EIKM là hình thoi
Lời giải
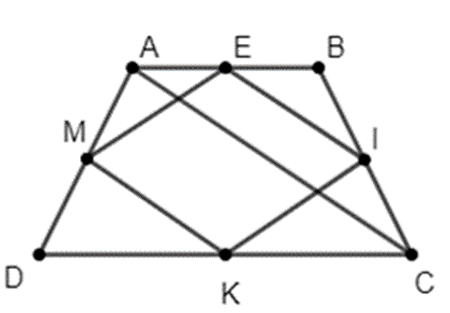
a) Xét tam giác ABC có E; I lần lượt là trung điểm của AB và BC.
Suy ra ta có EI là đường trung bình của tam giác ABC.
Do đó EI // AC, \(EI = \frac{1}{2}AC\) (1)
Chứng minh tương tự ta có: MK // AC, \(MK = \frac{1}{2}AC\) (2)
ME // BD, \(ME = \frac{1}{2}BD\) (3)
Mặt khác AC = BD (do tứ giác ABCD là hình thang cân) (4)
Từ (3) và (4) suy ra \[ME = \frac{1}{2}AC = MK\] (5)
Từ (1); (2); (5) suy ra tứ giác EIKM là hình thoi.
b) Để tứ giác EIMK là hình vuông thì EM ^ EI.
Mà theo câu a) ta có: EI // AC; EM // BD.
Khi đó suy ra để tứ giác EIMK là hình vuông thì AC ^ BD.
Lời giải
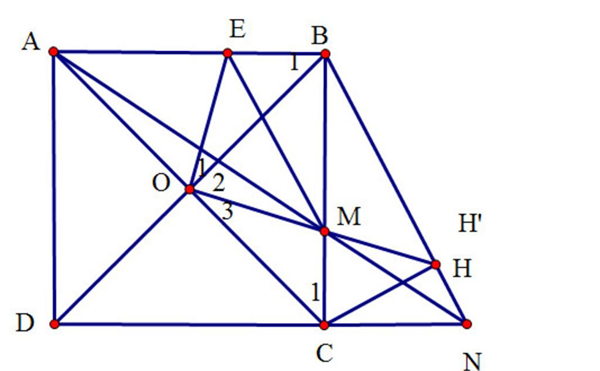
a) Xét ∆OEB và ∆OMC
Vi ABCD là hình vuông nên ta có: OB = OC
Và \[\widehat B = \widehat C = 45^\circ \]
BE = CM (gt)
Þ ∆OEB = ∆OMC (c.g.c)
Þ OE = OM và \({\widehat O_1} = {\widehat O_3}\)
Lại có: \({\widehat O_1} + {\widehat O_2} = \widehat {BOC} = 90^\circ \) vì tứ giác ABCD là hình vuông
\({\widehat O_1} + {\widehat O_2} = \widehat {EOM} = 90^\circ \) kết hợp với OE = OM
Þ ∆OEM vuông cân tại O.
b) Tứ giác ABCD là hình vuông Þ AB = CD và AB // CD
AB // CD Þ AB // CN \( \Rightarrow \frac{{AM}}{{MN}} = \frac{{BM}}{{MC}}\) (Theo định lý Ta-lét) (*)
Mà BE = CM (gt) và AB = CD Þ AE = BM thay vào (*)
Ta có: \[\frac{{AM}}{{MN}} = \frac{{AE}}{{EB}} \Rightarrow ME\;{\rm{//}}\;BN\] (theo định lý đảo Ta-lét)
c) Gọi H¢ là giao điểm của OM và BN
Từ ME // BN \[ \Rightarrow \widehat {OME} = \widehat {OH'E}\] (Cặp góc ở vị trí so le trong)
Mà \[\widehat {OME} = 45^\circ \] vì ∆OME vuông cân tại O
\( \Rightarrow \widehat {MH'B} = 45^\circ = \widehat {{C_1}}\)
Þ ∆OMC = ∆BMH¢ (g.g)
\( \Rightarrow \frac{{OM}}{{OB}} = \frac{{MH'}}{{MC}}\), kết hợp \( \Rightarrow \widehat {OMB} = \widehat {CMH'}\) (hai góc đối đỉnh)
Þ ∆OMB = ∆CMH¢ (c.g.c) \( \Rightarrow \widehat {OBM} = \widehat {MH'C} = 45^\circ \)
Vậy \(\widehat {BH'C} + \widehat {BH'M} + \widehat {MH'C} = 90^\circ \Rightarrow CH' \bot BN\)
Mà CH ^ BN (H Î BN) Þ H = H¢ hay 3 điểm O, M, H thẳng hàng (đpcm).
Lời giải
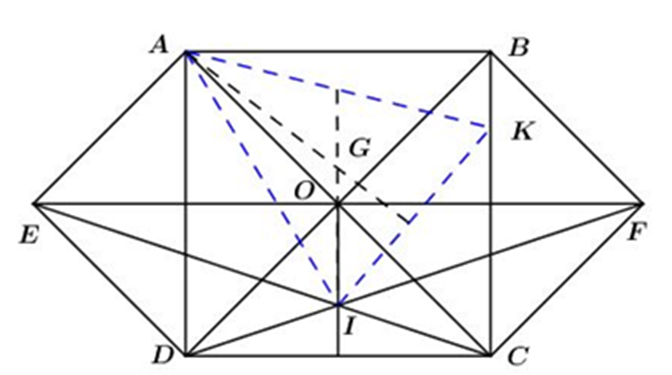
a) Gọi giao điểm của AD và EO là T
Giao điểm của BC và OF là H
Xét tứ giác EAOD có
\(\left. \begin{array}{l}AT = TD\\ET = TO\end{array} \right\} \Rightarrow EAOD\) là hình bình hành (dấu hiệu nhận biết).
Mà AD ^ EO nên tứ giác EAOD là hình thoi.
Hình thoi EAOD có \[\widehat {AOD} = 90^\circ \] nên là hình vuông.
Vậy EAOD là hình vuông theo dấu hiệu nhận biết hình thoi có 1 góc vuông.
Chứng minh tương tự với tứ giác OBFC.
b) Xét 2 tam giác ECF và FDE có:
\(\widehat {CFE} = \widehat {DEF} = 45^\circ \)
EF chung
FC = DE
Þ ΔECF = ∆FDE (c.g.c)
\( \Rightarrow \widehat {FEC} = \widehat {EFD}\)
Vậy tam giác EFI cân.
Mà O là trung điểm của EF Þ OI ^ EF (trong tam giác cân đường trung tuyến cũng là đường cao)
c) Ta có: ΔAED = ∆ABO = ∆BCO = ∆COD = ∆DOA = ∆BFC
SAED + SABO + SBCO + SCOD + SDOA + SBFC = SABFCDE = 6
Þ SABO = SBCO = SCOD = SDOA = 1
Þ SABCD = SABO + SBCO + SCOD + SDOA = 4
\( \Rightarrow AB = BC = CD = AD = \sqrt 4 = 2\)
d) Gọi M là giao điểm của IO với AB, N là giao điểm của IM với AK, ta có:
IO ^ FE Þ IO ^ AB Þ OM ^ AB, mà O là trung điểm của của HT nên M là trung điểm của AB.
Xét tam giác ABK có:
MA = MB (cmt)
MN // BK (vì MO // CD)
Do đó NA = NK
Þ N là trung điểm của AK
Þ IN là đường trung tuyến của ∆AIK.
Mà G là trọng tậm tam giác nên G Î IN
Þ G Î M với IM cố định (I, M cố định).
Vậy điểm G luôn nằm trên đường thẳng cố định IM.
Lời giải
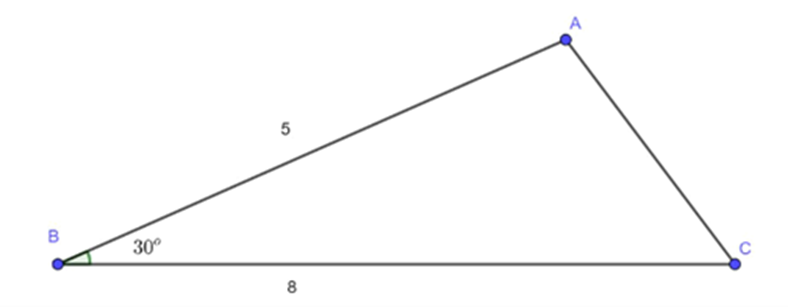
Diện tích tam giác ABC là:
\({S_{\Delta ABC}} = \frac{1}{2}AB\,.\,BC\,.\,\sin \widehat {ABC} = \frac{1}{2}\,.\,5\,.\,8\,.\,\sin 30^\circ = 10\;\left( {c{m^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \(\overrightarrow {AB} = \overrightarrow {DC} ;\)
B. \[\overrightarrow {OB} = \overrightarrow {DO} ;\]
C. \(\overrightarrow {OA} = \overrightarrow {OC} ;\)
D. \(\overrightarrow {CB} = \overrightarrow {DA} .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. \(\left| {\overrightarrow {HB} } \right| = \frac{a}{2};\)
B. \(\left| {\overrightarrow {AH} } \right| = \frac{{a\sqrt 3 }}{2};\)
C. \(\left| {\overrightarrow {CH} } \right| = \frac{{a\sqrt 3 }}{2};\)
D. \(\left| {\overrightarrow {BH} } \right| = \left| {\overrightarrow {HC} } \right|.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.